京东
今天的最新消息,京东又又又又又加薪了。
距离我们 京东宣布大幅上调校招薪资 的推文发布才一周多点的时间,京东又宣布加薪了。

好家伙,算上这次,光 2024 年京东就已经宣布了 6 次调薪了:
-
2024 年初,京东零售全员平均加薪不低于 20%; -
2024-01-01 起,京东采销等一线业务人员的年固定薪酬翻倍(平均涨幅 100%); -
2024-02-01 起,京东一线客服人员(超 2W 人)实现全年平均薪酬上涨 30%; -
2024-07-01 起,京东销售将用 18 个月时间,将年度固定薪酬从 16 薪提升至 20 薪,同时调整业绩激励上不封顶; -
2024 年 8 月,京东 2025 校园招聘全球启动,大幅上调校招薪资(算法岗平均起薪涨幅超 75%,硬件和设计等岗位起薪涨幅超 50%),开放 1.8W 个岗位招聘; -
2024-10-01,京东零售集团和职能体系将用两年时间实现 20 薪;
而且从本次的通告来看,京东的加薪行动还会不断持续。
这是比裁员"恶意"赔偿更加炸裂的行为,我愿称之为"恶意"加薪。
对此,你怎么看?
...
回归主题。
来一道和「京东」相关的算法原题。
题目描述
平台:LeetCode
题号:220
给你一个整数数组 nums 和两个整数 k 和 t。
请你判断是否存在两个不同下标 i 和 j,使得 abs(nums[i]-nums[j])<=t,同时又满足 abs(i-j)<=k 。
如果存在则返回 true,不存在返回 false。
示例 1:
输入:nums = [1,2,3,1], k = 3, t = 0
输出:true
示例 2:
输入:nums = [1,0,1,1], k = 1, t = 2
输出:true
示例 3:
输入:nums = [1,5,9,1,5,9], k = 2, t = 3
输出:false
提示:
滑动窗口 & 二分
根据题意,对于任意一个位置 i(假设其值为 u),我们其实是希望在下标范围为
内找到值范围在
的数。
一个朴素的想法是每次遍历到任意位置 i 的时候,往后检查 k 个元素,但这样做的复杂度是
的,会超时。
显然我们需要优化「检查后面 k 个元素」这一过程。
我们希望使用一个「有序集合」去维护长度为 k 的滑动窗口内的数,该数据结构最好支持高效「查询」与「插入/删除」操作:
-
查询:能够在「有序集合」中应用「二分查找」,快速找到「小于等于 的最大值」和「大于等于 u的最小值」(即「有序集合」中的最接近u的数)。 -
插入/删除:在往「有序集合」添加或删除元素时,能够在低于线性的复杂度内完成(维持有序特性)。
或许你会想到近似
操作的 HashMap,但注意这里我们需要找的是符合
的两个值,nums[i] 与 nums[j] 并不一定相等,而 HashMap 无法很好的支持「范围查询」操作。
我们还会想到「树」结构。
例如 AVL,能够让我们在最坏为
的复杂度内取得到最接近 u 的值是多少,但本题除了「查询」以外,还涉及频繁的「插入/删除」操作(随着我们遍历 nums 的元素,滑动窗口不断右移,我们需要不断的往「有序集合」中删除和添加元素)。
简单采用 AVL 树,会导致每次的插入删除操作都触发 AVL 的平衡调整,一次平衡调整会伴随着若干次的旋转。
而红黑树则很好解决了上述问题:将平衡调整引发的旋转的次数从「若干次」限制到「最多三次」。
因此,当「查询」动作和「插入/删除」动作频率相当时,更好的选择是使用「红黑树」。
也就是对应到 Java 中的 TreeSet 数据结构(基于红黑树,查找和插入都具有折半的效率)。
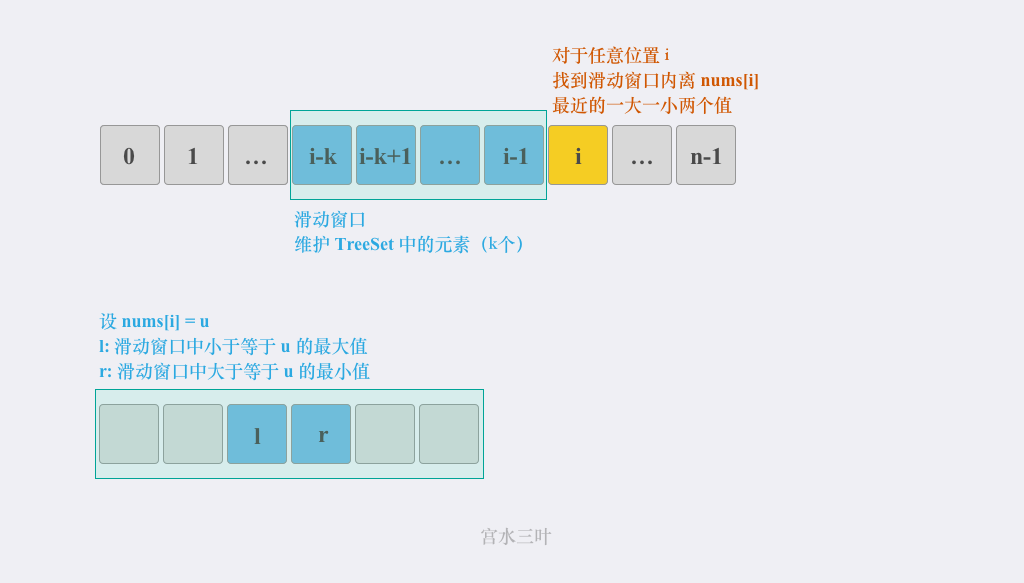
其他细节:由于 nums 中的数较大,会存在 int 溢出问题,我们需要使用 long 来存储。
Java 代码:
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
int n = nums.length;
TreeSet<Long> ts = new TreeSet<>();
for (int i = 0; i < n; i++) {
Long u = nums[i] * 1L;
// 从 ts 中找到小于等于 u 的最大值(小于等于 u 的最接近 u 的数)
Long l = ts.floor(u);
// 从 ts 中找到大于等于 u 的最小值(大于等于 u 的最接近 u 的数)
Long r = ts.ceiling(u);
if(l != null && u - l <= t) return true;
if(r != null && r - u <= t) return true;
// 将当前数加到 ts 中,并移除下标范围不在 [max(0, i - k), i) 的数(维持滑动窗口大小为 k)
ts.add(u);
if (i >= k) ts.remove(nums[i - k] * 1L);
}
return false;
}
}
C++ 代码:
class Solution {
public:
bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
int n = nums.size();
set<long long> ts;
for (int i = 0; i < n; i++) {
long long u = static_cast<long long>(nums[i]);
auto l = ts.lower_bound(u), r = ts.upper_bound(u);
if (l != ts.end() && *l - u <= t) return true;
if (r != ts.begin() && u - *(--r) <= t) return true;
ts.insert(u);
if (i >= k) ts.erase(static_cast<long long>(nums[i - k]));
}
return false;
}
};
Python 代码:
from sortedcontainers import SortedList
class Solution:
def containsNearbyAlmostDuplicate(self, nums, k, t):
n = len(nums)
ts = SortedList()
for i in range(n):
u = nums[i]
idx = ts.bisect_left(u)
if idx < len(ts) and ts[idx] - u <= t:
return True
if idx > 0 and u - ts[idx - 1] <= t:
return True
ts.add(u)
if i >= k:
ts.remove(nums[i - k])
return False
-
时间复杂度: TreeSet基于红黑树,查找和插入都是 复杂度。整体复杂度为 -
空间复杂度:
桶排序
上述解法无法做到线性的原因是:我们需要在大小为 k 的滑动窗口所在的「有序集合」中找到与 u 接近的数。
如果我们能够将 k 个数字分到
个桶的话,那么我们就能
的复杂度确定是否有
的数字(检查目标桶是否有元素)。
具体的做法为:令桶的大小为
,根据 u 计算所在桶编号:
-
如果已经存在该桶,说明前面已有 范围的数字,返回 true -
如果不存在该桶,则检查相邻两个桶的元素是有 范围的数字,如有 返回 true -
建立目标桶,并删除下标范围不在 内的桶
Java 代码:
class Solution {
long size;
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
int n = nums.length;
Map<Long, Long> map = new HashMap<>();
size = t + 1L;
for (int i = 0; i < n; i++) {
long u = nums[i] * 1L;
long idx = getIdx(u);
// 目标桶已存在(桶不为空),说明前面已有 [u - t, u + t] 范围的数字
if (map.containsKey(idx)) return true;
// 检查相邻的桶
long l = idx - 1, r = idx + 1;
if (map.containsKey(l) && u - map.get(l) <= t) return true;
if (map.containsKey(r) && map.get(r) - u <= t) return true;
// 建立目标桶
map.put(idx, u);
// 移除下标范围不在 [max(0, i - k), i) 内的桶
if (i >= k) map.remove(getIdx(nums[i - k] * 1L));
}
return false;
}
long getIdx(long u) {
return u >= 0 ? u / size : ((u + 1) / size) - 1;
}
}
C++ 代码:
class Solution {
public:
long long size;
bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
size = t + 1;
unordered_map<long long, long long> map;
int n = nums.size();
for (int i = 0; i < n; i++) {
long long u = static_cast<long long>(nums[i]);
long long idx = getIdx(u);
if (map.count(idx)) return true;
if (map.count(idx - 1) && u - map[idx - 1] <= t) return true;
if (map.count(idx + 1) && map[idx + 1] - u <= t) return true;
map[idx] = u;
if (i >= k) map.erase(getIdx(static_cast<long long>(nums[i - k])));
}
return false;
}
long long getIdx(long long u) {
return u >= 0 ? u / size : ((u + 1) / size) - 1;
}
};
Python 代码:
class Solution:
def containsNearbyAlmostDuplicate(self, nums, k, t):
size = t + 1
mapping = {}
for i, u in enumerate(nums):
idx = self.getIdx(u, size)
if idx in mapping:
return True
if (idx - 1) in mapping and u - mapping[idx - 1] <= t:
return True
if (idx + 1) in mapping and mapping[idx + 1] - u <= t:
return True
mapping[idx] = u
if i >= k:
del mapping[self.getIdx(nums[i - k], size)]
return False
def getIdx(self, u, size):
return u // size if u >= 0 else ((u + 1) // size) - 1;
-
时间复杂度: -
空间复杂度:
【重点】如何理解 getIdx() 的逻辑
-
为什么 size需要对t进行+1操作?
目的是为了确保差值小于等于 t 的数能够落到一个桶中。
举个 🌰,假设 [0,1,2,3],t = 3,显然四个数都应该落在同一个桶。
如果不对 t 进行 +1 操作的话,那么 [0,1,2] 和 [3] 会被落到不同的桶中,那么为了解决这种错误,我们需要对 t 进行 +1 作为 size 。
这样我们的数轴就能被分割成:
0 1 2 3 | 4 5 6 7 | 8 9 10 11 | 12 13 14 15 | …
总结一下,令 size = t + 1 的本质是因为差值为 t 两个数在数轴上相隔距离为 t + 1,它们需要被落到同一个桶中。
当明确了 size 的大小之后,对于正数部分我们则有 idx = nums[i] / size。
-
如何理解负数部分的逻辑?
由于我们处理正数的时候,处理了数值 0,因此我们负数部分是从 -1 开始的。
还是我们上述 🌰,此时我们有 t = 3 和 size = t + 1 = 4。
考虑 [-4,-3,-2,-1] 的情况,它们应该落在一个桶中。
如果直接复用 idx = nums[i] / size 的话,[-4] 和 [-3,-2,-1] 会被分到不同的桶中。
根本原因是我们处理整数的时候,已经分掉了数值 0。
这时候我们需要先对 nums[i] 进行 +1 操作(即将负数部分在数轴上进行整体右移),即得到 (nums[i] + 1) / size。
这样一来负数部分与正数部分一样,可以被正常分割了。
但由于 0 号桶已经被使用了,我们还需要在此基础上进行 -1,相当于将负数部分的桶下标(idx)往左移,即得到 ((nums[i] + 1) / size) - 1。
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉