这篇笔记可以作为接EoT那篇笔记内容中某种思想内涵的延伸和实践,即均是将智能体之间的关系描述为一种拓扑连接结构下的网络化关系进行研究(贴近物理世界更加真实、自然、客观的拓扑结构),在这项研究中,更多的扩展到大规模真实世界多智能体系统中来,如更复杂的交通信号灯或电网传输动态规划与控制。
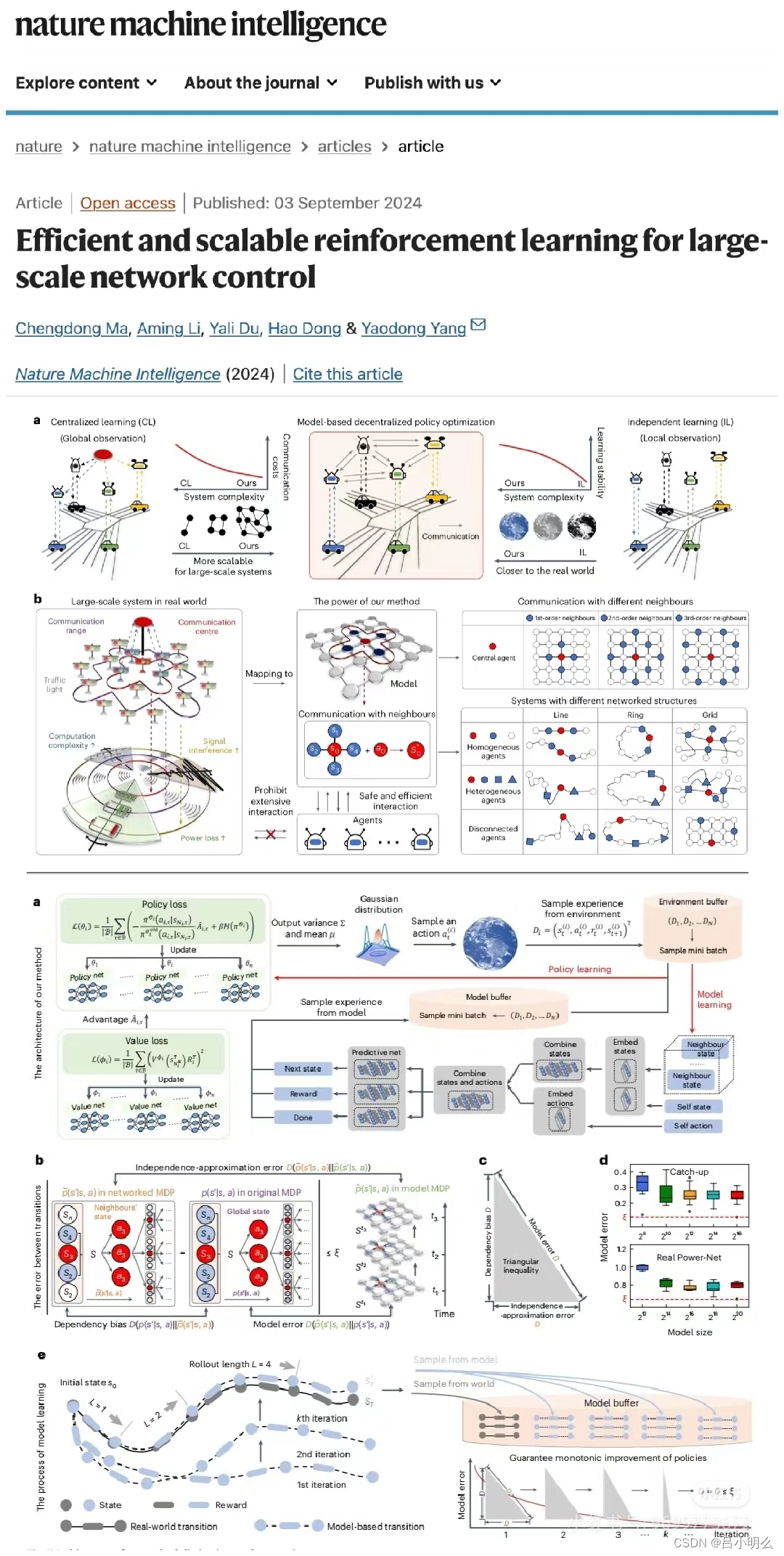
另外,这项研究的另一核心出发点聚焦在:降低了现有多智能体学习方法对于全局通信和大量交互数据的依赖性,尝试验证强化学习算法在复杂的大规模系统中的局部优化分解下的广泛部署与高效扩展,并朝着可扩展到大规模系统的决策范式迈出了重要一步,并于去中心化模型学习和单调策略提升之间建立了重要的理论桥梁。
具体的,在这项研究中研究团队对大规模多智能体系统进行了以智能体为单位的动力学特性的解耦,将智能体之间的关系描述为一种拓扑连接结构下的网络化关系,其中包括线状,环状,网状等各种同构 / 异构节点,降低了系统处理的复杂性。
在此之前,也有一些研究者以网络化的形式建模智能体之间的关系从而提升算法扩展性。但这种对于系统的分解具有较强的假设,不一定符合真实世界系统的特性。
因此团队进一步提出了一种更通用的网络化系统模型用来刻画解耦后多智能体系统的动力学和真实系统动力学之间的关系,其优势在于它能够处理更广泛的合作多智能体任务。该概念弥合了标准网络系统和一般多代理系统之间的差距,为去中心化多智能体系统的研究提供了必要的理论框架和分析工具。
其中,我认为这项研究的一个关键思想假设尤为重要:即仅通过接收相邻路口的车流信息调控复杂的交通流是有效的。这是因为在网络化结构的设计下,整体交通状况已经通过城市路网以上述某种拓扑链数据形式间接地传递并汇总到相邻路口,通过分析这些相邻路口的观测信息,就能推断和预测整个城市的车流变化,从而做出最优决策。
其中在智能电网上的效果也验证了方法的可扩展性,能够在具有上百个节点的电力网络中实现较低的电能损耗...
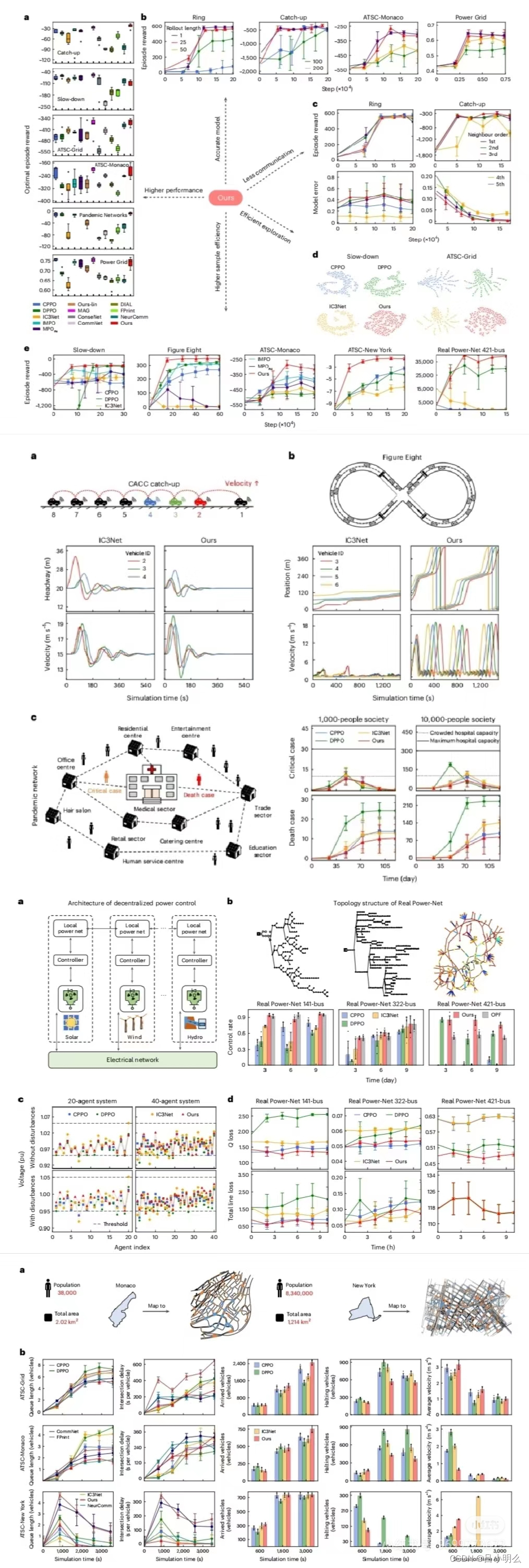
大家有兴趣的话可以详细阅读一下这篇论文,另外,我想记录这篇笔记的初衷也与EoT那篇笔记一样,期望更多的这一领域的研究和探索者们在Multi-agent快速发展的当下,看是否额外做一些思考延展以关注真实世界下不同拓扑结构、组织形式、被赋予不同内涵的Agent个体与群体间通信协作下的底层差异和通用泛化性。
#人工智能 #AGI #LLM #智能体 #多智能体 #多智能体强化学习 #强化学习