目录
一、Prim算法
二、题目与题解
题目:卡码网 53. 寻宝
题目链接
题解1:Prim算法
题解2:Prim算法优化
题解3:Kruskal算法
三、小结
一、Prim算法与Kruskal算法
Prim算法是一种贪心算法,用于求解加权无向图的最小生成树问题。其中,最小生成树是指一个边的子集,它连接图中的所有顶点,且边的总权重最小,并且没有形成环。
Kruskal算法是一种用于寻找加权无向图的最小生成树的贪心算法。所谓最小生成树,是指在保证图中的所有顶点都通过边相连的前提下,所有边的权重之和最小的树形结构。
对于Prim算法和Kruskal算法的简单了解,这里推荐看看:【图-最小生成树-Prim(普里姆)算法和Kruskal(克鲁斯卡尔)算法】
二、题目与题解
题目:卡码网 53. 寻宝
题目链接
53. 寻宝(第七期模拟笔试) (kamacoder.com)
题目描述
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来(注意:这是一个无向图)。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述
输出联通所有岛屿的最小路径总距离
输入示例
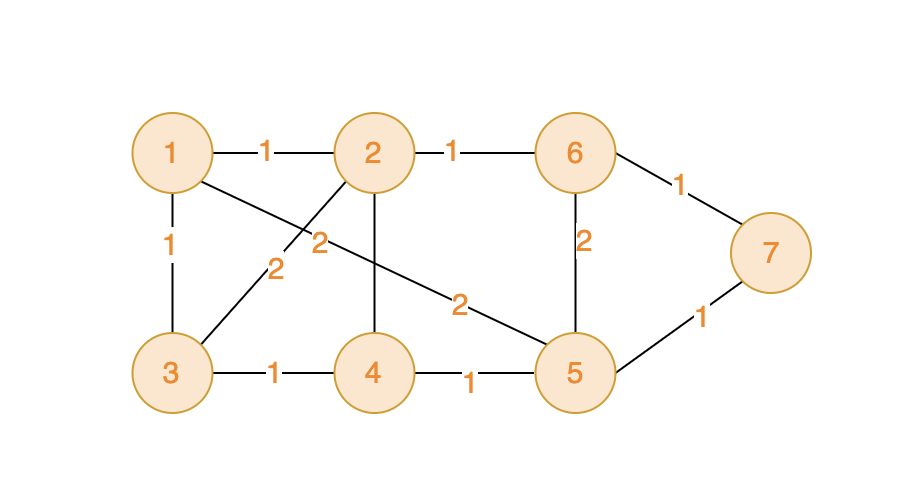
7 11 1 2 1 1 3 1 1 5 2 2 6 1 2 4 2 2 3 2 3 4 1 4 5 1 5 6 2 5 7 1 6 7 1输出示例
6提示信息
数据范围:
2 <= V <= 10000;
1 <= E <= 100000;
0 <= val <= 10000;如下图,可见将所有的顶点都访问一遍,总距离最低是6.
题解1:Prim算法
建议先看视频了解了Prim算法的实现步骤再看以下思路和步骤。
基本思路:
1.选择一个起始顶点,将其标记为已访问,并将其距离设置为0,其他顶点的距离设置为无穷大
2.创建一个循环,直到所有顶点都被访问:
初始化一个变量来记录当前最小边的权重,将其设置为无穷大。
初始化两个变量来记录最小边的两个顶点。
3.遍历所有已访问顶点,对于每个已访问顶点,遍历它的所有邻接顶点:
如果邻接顶点未被访问,并且连接这两个顶点的边的权重小于当前记录的最小边权重,则更新最小边权重和对应的两个顶点。
将找到的最小边加入到最小生成树中,并标记连接的非最小生成树顶点为已访问。 更新该顶点的所有邻接顶点到最小生成树的最短距离。
4.当所有顶点都被访问后,算法结束,此时最小生成树由记录的所有边组成。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int v, e;
int x, y, k;
cin >> v >> e; // 输入顶点数v(注意范围是:1 - v)和边数e
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001)); // 二维数组grid,用于存储图的邻接矩阵,初始值为10001(表示无穷大)
while (e--)
{
cin >> x >> y >> k; // 输入边的两个顶点和权值
// 因为是双向图,所以两个方向都要填上
grid[x][y] = k;
grid[y][x] = k;
}
// 用于存储每个顶点到最小生成树的最短距离 -- 由于顶点数为v,这里大小设置为v+1
vector<int> minDist(v + 1, 10001);
// 初始化第一个顶点到最小生成树的距离为0
minDist[1] = 0;
// 用于标记顶点是否已经在最小生成树中
vector<bool> isInTree(v + 1, false);
// 我们只需要循环 n-1次,因为最小生成树有v-1条边,这样就可以把n个节点的图连在一起
for (int i = 1; i < v; i++)
{
// 选择距离最小生成树最近的顶点
int cur = -1; // 当前选中的顶点 -- 最终选中的cur节点即是加入最小生成树的最近节点
int minVal = INT_MAX; // 当前最小距离,初始化为无穷大
for (int j = 1; j <= v; j++) // 顶点编号:1 - v
{
if (!isInTree[j] && minDist[j] < minVal) // 选择不在最小生成树中且距离最小的顶点
{
minVal = minDist[j];
cur = j;
}
}
// 最近节点(cur)加入生成树
isInTree[cur] = true;
// 更新非生成树节点到生成树的距离(即更新minDist数组):由于新加入了cur节点,这里只需要多考虑cur与不在最小生成树的节点的距离即可
for (int j = 1; j <= v; j++)
{
if (!isInTree[j] && grid[cur][j] < minDist[j]) // 如果顶点j不在生成树中,并且通过cur到j的距离小于当前记录的最短距离,则更新
{
minDist[j] = grid[cur][j];
}
}
}
int ans = 0; // 统计结果
for (int i = 2; i <= v; i++) // 累加每个顶点到生成树的最短距离,注意从第二个顶点开始累加,因为第一个顶点距离为0
{
ans += minDist[i];
}
cout << ans << endl;
}题解2:Prim算法优化
这题还可以用优先队列(堆)进行优化,这也是Prim算法最经典的使用方法:
算法思路:
PRIM(G, w, s):
1. for each u in G.V:
u.key = INFINITY
u.pi = NIL
2. s.key = 0
3. Q = G.V (创建一个顶点的优先队列,初始时包含所有顶点)
4. while Q is not empty:
u = EXTRACT-MIN(Q) (从Q中取出具有最小key值的顶点)
for each v in G.Adj[u]: (遍历顶点u的所有邻接顶点v)
if v in Q and w(u, v) < v.key:
v.pi = u
v.key = w(u, v)
其中:G表示图,w表示边的权重函数,s是起始顶点。u.key表示顶点u到最小生成树的最短边权重,u.pi表示在最小生成树中顶点u的前驱顶点。
代码如下:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int v, e;
cin >> v >> e; // 输入顶点数v和边数e
// 使用邻接矩阵存储图的边信息,初始化为无穷大
vector<vector<int>> grid(v + 1, vector<int>(v + 1, INT_MAX));
// 读取边的信息
for (int i = 1; i <= e; ++i)
{
int x, y, k;
cin >> x >> y >> k; // 输入边的两个顶点和权值
grid[x][y] = k;
grid[y][x] = k;
}
// 使用优先队列来存储顶点及其到最小生成树的最短距离
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
// 用于存储每个顶点到最小生成树的最短距离,初始化为无穷大
vector<int> minDist(v + 1, INT_MAX);
minDist[1] = 0; // 第一个顶点到最小生成树的距离为0
// 标记顶点是否已经在最小生成树中
vector<bool> isInTree(v + 1, false);
// 将第一个顶点加入优先队列
pq.push({0, 1});
while (!pq.empty())
{
// 从优先队列中取出距离最小生成树最近的顶点
int cur = pq.top().second;
pq.pop();
// 如果该顶点已经在最小生成树中,则跳过
if (isInTree[cur])
continue;
// 将该顶点标记为已加入最小生成树
isInTree[cur] = true;
// 更新邻接顶点到最小生成树的最短距离
for (int j = 1; j <= v; ++j)
{
if (!isInTree[j] && grid[cur][j] < minDist[j])
{
minDist[j] = grid[cur][j];
pq.push({minDist[j], j}); // 将更新后的顶点和距离加入优先队列
}
}
}
// 计算最小生成树的总权重
int ans = 0;
for (int i = 2; i <= v; ++i)
{
ans += minDist[i];
}
cout << ans << endl; // 输出最小生成树的总权重
return 0;
}题解3:Kruskal算法
对应Kruskal算法,一般按照以下思路进行:
KRUSKAL(G)算法思路:
1. 将G中的所有边按权重从小到大排序。
2. 初始化森林F,使得每个顶点都是一个独立的树。
3. for each 边(u, v) in G的边列表,按权重从小到大:
a. 查找u所在的树的根节点。
b. 查找v所在的树的根节点。
c. if u和v的根节点不同(即不会形成环):
i. 将边(u, v)加入森林F。
ii. 合并u和v所在的树。
4. 返回森林F,即为最小生成树。
其中某些步骤的实现即是前缀和的几个基本操作,之前有提到,这里不多做解释。
代码如下:
#include <bits/stdc++.h>
using namespace std;
int n = 1001;
vector<int> father(n, 0); // 并查集数组:节点编号是从1开始的
// l,r为 边两边的节点,val为边的数值
struct Edge
{
int l, r, val;
};
// 并查集初始化
void init()
{
for (int i = 1; i <= n; i++)
father[i] = i;
}
// 并查集里寻找该节点的根节点(带路径压缩)
int find(int u)
{
if (u != father[u])
father[u] = find(father[u]);
return father[u];
}
// join 函数用于合并两个节点所在的集合:将v-u这条边加入并查集
void join(int u, int v)
{
int rootu = find(u);
int rootv = find(v);
if (rootu != rootv)
father[rootv] = rootu;
}
int main()
{
int v, e;
int v1, v2, val;
vector<Edge> edges; // edges数组存放所有边 -- 每个元素都是Edge结构(l,r,val)
int ans = 0;
cin >> v >> e;
while (e--)
{
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
// Kruskal算法
// 1.按边的权值对边进行从小到大排序
sort(edges.begin(), edges.end(), [](const Edge &a, const Edge &b)
{ return a.val < b.val; });
// 2.并查集初始化
init();
for (Edge edge : edges) // 3.从头开始遍历边:按边的权重从小到大
{
// 4.并查集,搜出两个节点u和v所在树的根节点 -- 确保不会形成环
int rootu = find(edge.l);
int rootv = find(edge.r);
// 5.如果u,v根节点不同 -- 即不会形成环(注意)
if (rootu != rootv)
{
ans += edge.val; // 6.这条边u-v加入生成树
join(rootu, rootv); // 7.合并u,v所在的树:两个节点加入到同一个集合
}
}
cout << ans << endl;
return 0;
}三、小结
至此完善了这天的打卡,后边会继续加油!