算法工程师重生之第六天（四数相加II 赎金信三数之和四数之和总结）

参考文献代码随想录

一、四数相加 II

给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：

0 <= i, j, k, l < n
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

示例 1：

输入：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出：2
解释：
两个元组如下：
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0

示例 2：

输入：nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出：1

提示：

n == nums1.length
n == nums2.length
n == nums3.length
n == nums4.length
1 <= n <= 200
-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228

问题分析

最开始的想法就是4个循环然后统计等于0的个数，但是会超时，那么该如何优化呢？我们使用字典存储，因为查询的时间复杂度为o(1)，就是key是2个数组元素的和，而value为对应出现的次数，然后在遍历另外2个数组，统计它们的相反数，因为这样，才能等于0，那如何统计它们的相反数呢，就是查询它们相反数在字典中的次数。为什么不可以先遍历一个数组，然后在遍历3个数组呢？这样来，时间复杂度为n的立方。

而这道题目是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于题目18. 四数之和，题目15.三数之和，还是简单了不少！

如果本题想难度升级：就是给出一个数组（而不是四个数组），在这里找出四个元素相加等于0，答案中不可以包含重复的四元组，大家可以思考一下，后续的文章我也会讲到的。

本题解题步骤：

首先定义一个unordered_map，key放a和b两数之和，value 放a和b两数之和出现的次数。
遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中。
定义int变量count，用来统计 a+b+c+d = 0 出现的次数。
再遍历大C和大D数组，找到如果 0-(c+d) 在map中出现过的话，就用count把map中key对应的value也就是出现次数统计出来。
最后返回统计值 count 就可以了

class Solution(object):
    def fourSumCount(self, nums1, nums2, nums3, nums4):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :type nums3: List[int]
        :type nums4: List[int]
        :rtype: int
        """
        from collections import  defaultdict
        sumAB = defaultdict(int)  # 这个是动态，int 代表的是里面的元素为整型，如果是List，那么里面的元素是list类型
        count = 0
        
        # 计算所有 nums1[i] + nums2[j] 的和并记录出现次数
        for i in nums1:
            for j in nums2:
                sumAB[i + j] += 1
        
        # 计算所有 nums3[k] + nums4[l] 的和，查找其负数是否在 sumAB 中
        for k in nums3:
            for l in nums4:
                count += sumAB[-(k + l)]
        
        return count

二、赎金信

给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成。

如果可以，返回 true ；否则返回 false 。

magazine 中的每个字符只能在 ransomNote 中使用一次。

示例 1：

输入：ransomNote = "a", magazine = "b"
输出：false

示例 2：

输入：ransomNote = "aa", magazine = "ab"
输出：false

示例 3：

输入：ransomNote = "aa", magazine = "aab"
输出：true

提示：

1 <= ransomNote.length, magazine.length <= 105
ransomNote 和 magazine 由小写英文字母组成

问题分析

先统计magazine各个字母出现的次数，然后在统计ransomNote每个字母出现的次数左减法

class Solution(object):
    def canConstruct(self, ransomNote, magazine):
        """
        :type ransomNote: str
        :type magazine: str
        :rtype: bool
        """
        dic = defaultdict(int)
        for i in magazine:
            dic[i] += 1
        for j in ransomNote:
            dic[j] -= 1
        for key in dic:
            if dic[key] < 0:
                return False
        return True

三、三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

问题分析

而且使用哈希法在使用两层for循环的时候，能做的剪枝操作很有限，虽然时间复杂度是O(n^2)，也是可以在leetcode上通过，但是程序的执行时间依然比较长。

接下来我来介绍另一个解法：双指针法，这道题目使用双指针法要比哈希法高效一些，那么来讲解一下具体实现的思路。

动画效果如下：

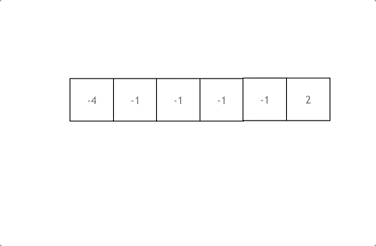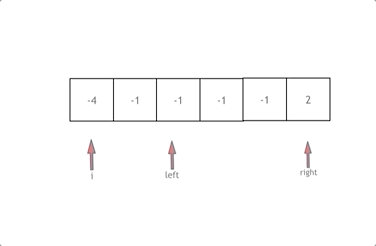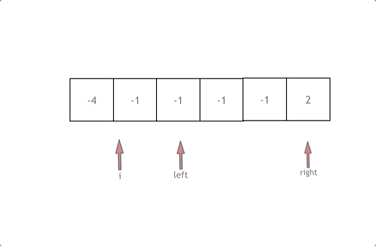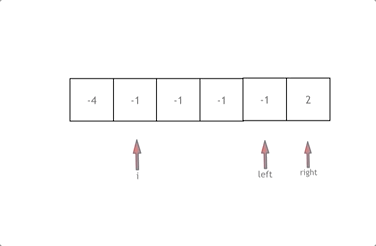
15.三数之和

拿这个nums数组来举例，首先将数组排序，然后有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。

依然还是在数组中找到 abc 使得a + b +c =0，我们这里相当于 a = nums[i]，b = nums[left]，c = nums[right]。

接下来如何移动left 和right呢，如果nums[i] + nums[left] + nums[right] > 0 就说明此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。

如果 nums[i] + nums[left] + nums[right] < 0 说明此时三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。

去重逻辑的思考

#a的去重

说到去重，其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i]，nums[left]，nums[right]

a 如果重复了怎么办，a是nums里遍历的元素，那么应该直接跳过去。

但这里有一个问题，是判断 nums[i] 与 nums[i + 1]是否相同，还是判断 nums[i] 与 nums[i-1] 是否相同。

有同学可能想，这不都一样吗。

其实不一样！

都是和 nums[i]进行比较，是比较它的前一个，还是比较它的后一个。

如果我们的写法是这样：

if (nums[i] == nums[i + 1]) { // 去重操作
    continue;
}

那我们就把三元组中出现重复元素的情况直接pass掉了。例如{-1, -1 ,2} 这组数据，当遍历到第一个-1 的时候，判断下一个也是-1，那这组数据就pass了。

我们要做的是不能有重复的三元组，但三元组内的元素是可以重复的！

所以这里是有两个重复的维度。

那么应该这么写：

if (i > 0 && nums[i] == nums[i - 1]) {
    continue;
}

这么写就是当前使用 nums[i]，我们判断前一位是不是一样的元素，在看 {-1, -1 ,2} 这组数据，当遍历到第一个 -1 的时候，只要前一位没有-1，那么 {-1, -1 ,2} 这组数据一样可以收录到结果集里。

这是一个非常细节的思考过程。

#b与c的去重

很多同学写本题的时候，去重的逻辑多加了对right 和left 的去重：（代码中注释部分）

while (right > left) {
    if (nums[i] + nums[left] + nums[right] > 0) {
        right--;
        // 去重 right
        while (left < right && nums[right] == nums[right + 1]) right--;
    } else if (nums[i] + nums[left] + nums[right] < 0) {
        left++;
        // 去重 left
        while (left < right && nums[left] == nums[left - 1]) left++;
    } else {
    }
}

但细想一下，这种去重其实对提升程序运行效率是没有帮助的。

拿right去重为例，即使不加这个去重逻辑，依然根据 while (right > left) 和 if (nums[i] + nums[left] + nums[right] > 0) 去完成right-- 的操作。

多加了 while (left < right && nums[right] == nums[right + 1]) right--; 这一行代码，其实就是把需要执行的逻辑提前执行了，但并没有减少判断的逻辑。

最直白的思考过程，就是right还是一个数一个数的减下去的，所以在哪里减的都是一样的。

所以这种去重是可以不加的。仅仅是把去重的逻辑提前了而已。

#思考题

既然三数之和可以使用双指针法，我们之前讲过的1.两数之和 (opens new window)，可不可以使用双指针法呢？

如果不能，题意如何更改就可以使用双指针法呢？ 大家留言说出自己的想法吧！

两数之和就不能使用双指针法，因为1.两数之和 (opens new window)要求返回的是索引下标，而双指针法一定要排序，一旦排序之后原数组的索引就被改变了。

如果1.两数之和 (opens new window)要求返回的是数值的话，就可以使用双指针法了。

主要是，在一个数组里找出不同的三元组，但是三元组里面的元素可以重复，这里使用的是相对于3个指针，来找对应的值是否为零，就是一个for加一个双指针，那么该如何去寻找呢、首先，对数组排序，为什么要排序呢？答案是：如果你不排序，你不知道如何移动双指针的方向，就是你判断了这个3个指针对应数值的和后，如果是小于0，那么双指针的2个指针该移动到右还是做呢？（不知道那边是大是小），for循环已经固定了，然后如果第一个元素大于0，那么就直接pass，我们是不是要对当前的指针去重，是根已经遍历过的去重，还是for循环接下来的数呢？我们这里三元组里面的元素是可以重复的，所以你如果根接下来的数判断的话，那是不是就丢掉了三元组元素重复的值呢？例如[-1,-1,2]当前for循环指向到下标为0的地方，然后这时你与下标为1的元素判断，那么是不是被pass呢？所以要根遍历过的元素作比较，因为遍历过的元素很有可能在结果集里面，比较的同时要保证下标大于0，防止下标出界，接下来就说是left和right，left就去i的下一个元素，而right取到最后元素的下标，就是素组长度减一，然后循环去移动left和right，那么条件该是什么呢？是大于等于呢，还是大于，结果是大于，为什么？因为如果你等于，那么元素就很有可能出现只有2个元素的情况，如果3个对应的值大于0，那么该移动left？还是right？结果是移动right，为什么，因为right在三个对应值中最大的，所以要移动right，如果小于零那么就移动left和right小的那个，最后等于0了，就要收集结果了，还会出现，2种情况，就是right和后面的元素相等，left和前面的元素相等，这里要使用while判断，因为不可能相同的元素只有2个，很有可能有多个存在。

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        nums.sort() # 这个是为了后面好去重，这里的思想主要是一个for代表一个元素，另外2个指针
        result = []
        for i in range(len(nums)):
            if nums[i] > 0: # 如果第一个元素都大于0了，那么后面的元素肯定大于0，因为素组是排好序的，升序
                return result
            # 这里要对nums[i] 去重
            if i > 0 and nums[i] == nums[i - 1]:  # 为什么要根后一个比呢，因为后一个值已经遍历过了，如果你根i+1比的话，这就对三元组里面的元素去重了，因为i到right之间的数都有可能成为三元组，
                continue
            left = i + 1
            rigth = len(nums) - 1
            while rigth > left: #这里为什么不能取等号呢，如果你去等好的话，会出先2个元素
                if nums[i] + nums[left] + nums[rigth] > 0: # 如果大于0，那么就尽可能的减小，因为出现0的只会在right之前
                    rigth -= 1
                elif nums[i] + nums[left] + nums[rigth] < 0: # 如果小于0，那么就慢慢给它增加，这样才能最大可能获取到三元组
                    left += 1
                else:
                    result.append([nums[i] , nums[left],nums[rigth]])
                    while rigth > left and nums[rigth] == nums[rigth - 1]:  # 对right去重，为什么不使用if，因为有可能移动后还是相同的数，因为此时的rigth的下标，已经添加到结果集了
                        rigth -= 1
                    while rigth > left and nums[left] == nums[left + 1]: # 对left去重
                        left += 1
                    rigth -= 1
                    left += 1
        return result

四、四数之和

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

提示：

1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109

问题分析

数之和，和15.三数之和 (opens new window)是一个思路，都是使用双指针法, 基本解法就是在15.三数之和 (opens new window)的基础上再套一层for循环。

但是有一些细节需要注意，例如：不要判断nums[k] > target 就返回了，三数之和可以通过 nums[i] > 0 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。比如：数组是[-4, -3, -2, -1]，target是-10，不能因为-4 > -10而跳过。但是我们依旧可以去做剪枝，逻辑变成nums[i] > target && (nums[i] >=0 || target >= 0)就可以了。

15.三数之和 (opens new window)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下标作为双指针，找到nums[i] + nums[left] + nums[right] == 0。

四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。

那么一样的道理，五数之和、六数之和等等都采用这种解法。

对于15.三数之和 (opens new window)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。

之前我们讲过哈希表的经典题目：454.四数相加II (opens new window)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。

而454.四数相加II (opens new window)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！

我们来回顾一下，几道题目使用了双指针法。

双指针法将时间复杂度：O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下：

27.移除元素(opens new window)
15.三数之和(opens new window)
18.四数之和(opens new window)

链表相关双指针题目：

206.反转链表(opens new window)
19.删除链表的倒数第N个节点(opens new window)
面试题 02.07. 链表相交(opens new window)
142题.环形链表II(opens new window)

双指针法在字符串题目中还有很多应用，后面还会介绍到。

class Solution(object):
    def fourSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        nums.sort()
        n = len(nums)
        result = []
        for i in range(n):
            if nums[i] > target and nums[i] > 0 and target > 0:# 剪枝（可省）只有都大于0，才能判断，如果小于0，就不可以
                break
            if i > 0 and nums[i] == nums[i-1]:# 去重
                continue
            for j in range(i+1, n):
                if nums[i] + nums[j] > target and target > 0: #剪枝（可省）
                    break
                if j > i+1 and nums[j] == nums[j-1]: # 去重
                    continue
                left, right = j+1, n-1
                while left < right:
                    s = nums[i] + nums[j] + nums[left] + nums[right]
                    if s == target:
                        result.append([nums[i], nums[j], nums[left], nums[right]])
                        while left < right and nums[left] == nums[left+1]:
                            left += 1
                        while left < right and nums[right] == nums[right-1]:
                            right -= 1
                        left += 1
                        right -= 1
                    elif s < target:
                        left += 1
                    else:
                        right -= 1
        return result

五、哈希表总结

一般来说哈希表都是用来快速判断一个元素是否出现集合里。

对于哈希表，要知道哈希函数和哈希碰撞在哈希表中的作用。

哈希函数是把传入的key映射到符号表的索引上。

哈希碰撞处理有多个key映射到相同索引上时的情景，处理碰撞的普遍方式是拉链法和线性探测法。

接下来是常见的三种哈希结构：

数组
set（集合）
map（映射）

#哈希表经典题目

#数组作为哈希表

一些应用场景就是为数组量身定做的。

在242.有效的字母异位词 (opens new window)中，我们提到了数组就是简单的哈希表，但是数组的大小是受限的！

这道题目包含小写字母，那么使用数组来做哈希最合适不过。

在383.赎金信 (opens new window)中同样要求只有小写字母，那么就给我们浓浓的暗示，用数组！

本题和242.有效的字母异位词 (opens new window)很像，242.有效的字母异位词 (opens new window)是求字符串a 和字符串b 是否可以相互组成，在383.赎金信 (opens new window)中是求字符串a能否组成字符串b，而不用管字符串b 能不能组成字符串a。

一些同学可能想，用数组干啥，都用map不就完事了。

上面两道题目用map确实可以，但使用map的空间消耗要比数组大一些，因为map要维护红黑树或者符号表，而且还要做哈希函数的运算。所以数组更加简单直接有效！