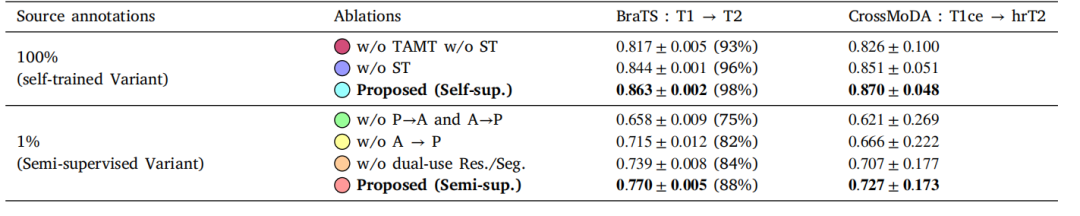
快速导航
- 一、树的基础概念
- 1. 树的定义:
- 2. 树的特点:
- 3. 树的常用术语:
- 4. 树的简单分类:
- 二、树的存储结构
- 1.顺序存储
- 1) 双亲表示法
- 2) 孩子表示法
- 3) 双亲孩子表示法
- 2.链式存储
- 1) 孩子链表表示法
- 2) 孩子兄弟表示法
- 三、树、森林和二叉树的转换
- 1. 树和二叉树的互相转换
- 2. 森林和二叉树的互相转化:
一、树的基础概念
1. 树的定义:
树(tree)是n(n≥0)个节点的有限集合,
当n=0时,为空树;n>0时,为非空树。任意一棵非空树,满足以下两个条件:
1)有且仅有一个称为根的节点;
2)除根节点以外,其余节点可分为m(m>0)个互不相交的有限集T1,T2, …,Tm,其中每一个集合本身又是一棵树,并且称为根的子树(subtree)。
下图是一棵树的例子:

2. 树的特点:
不同于链表、数组等线性结构,
- 树通常用于表示一对多的关系
- 除了树根节点之外,每一个节点只有一个直接前驱
- 除了叶子节点之外,每一个节点都有一个或多个直接后继
3. 树的常用术语:
节点:树的组成单位,包含数据元素和若干指向子树的分支信息节点的度:节点拥有的子树个数树的度:树中节点的最大度终端节点:度为0的节点,即叶子节点分支节点:度大于0的节点,除了叶子节点都是分支节点内部节点:除了树根和叶子都是内部节点
下图是对上面术语的展示的一棵树:

节点的层次:从根到该节点的层数(根节点为第一层)树的深度(或高度):指所有节点中最大的层数路径:树中两个节点之间经过的节点列表路径长度:路径上包含的边数
4. 树的简单分类:
-
有序树:节点的各子树从左到右有序,不能互换位置

-
无序树:节点的各子树可互换位置 -
森林:由m(m≥0)棵不相交的树组成的集合
二、树的存储结构
树的存储特点:不仅需要存储数据元素,还需要存储节点之间的逻辑关系,即指针。
树的存储结构主要有两种:顺序存储 和 链式存储
1.顺序存储
顺序存储的特点 :存储空间是一段连续的内存
顺序存储分为:双亲表示法、孩子表示法和双亲孩子表示法
1) 双亲表示法
双亲表示法,除了存储数据元素之外,还存储双亲节点的存储位置下标。
特点:
- 只记录了每个节点的双亲,无法直接得到孩子节点。
2) 孩子表示法
孩子表示法,除存储数据元素之外,还存储所有孩子节点的存储位置下标。
特点:
- 只记录了所有的孩子节点,无法直接得到双亲。
- 由于不知道每个节点有多少个孩子,只能按照树的度分配空间,可能会浪费很多空间。
3) 双亲孩子表示法
双亲孩子表示法,是上面两种表示法的结合体,除存储数据之外,还存储了双亲节点和所有孩子节点的存储下标。
特点:
- 可以直接找到双亲节点和所有的孩子节点
- 和孩子表示法一样,可能浪费很多空间
2.链式存储
1) 孩子链表表示法
思路:邻接表。将节点的所有孩子存储在一个单链表中
孩子链表表示法的图示:

特点:
- 表头包含元素,并指向第一个孩子指针,将所有的孩子放入单链表
- 在表头中data存储数据元素,frist存储指向第一个孩子的指针
- 单链表中的节点记录该节点的下标和下一个节点的地址
变种: 双亲孩子链表表示法。
调整方法: 在孩子链表表示法的表头增加一个双亲域。
2) 孩子兄弟表示法
思路:二叉链表。左指针存储第一个孩子,右指针存储兄弟
孩子兄弟表示法图示:

特点:
- 节点除了存储数据元素之外,还有两个指向其他节点的指针。
- 左指针指向第一个孩子,右指针指向最近的兄弟
存储转化图示:

秘诀: 长子当作左孩子,兄弟关系向右斜。
三、树、森林和二叉树的转换
1. 树和二叉树的互相转换
从上面的孩子兄弟表示法得到灵感,所有的树都可以通过孩子兄弟表示法转换成为二叉树。
树转换成二叉树:

而同样的,反操作一下,即可从二叉树还原为树。
二叉树还原为树:

2. 森林和二叉树的互相转化:
森林也是如此,转化过程中并没有要求必须是一棵树,只需要关注第一个孩子和兄弟。把森林中的多棵树的根节点作为兄弟,即可实现森林到二叉树的转化。
森林转化成二叉树:

二叉树转化成森林:

参考资料:《趣学数据结构》 – 陈小玉