前言
代理模型工具箱 (surrogate modeling toolbox, SMT) 是一个基于Python开发的第三方包,其中包含代理模型方法、采样技术和基准测试函数。有关SMT的详细介绍参见:
SMT | 代理模型Python工具包推荐
SMT可实现几个与高斯过程回归相关的代理模型:
- Kriging (KRG):经典的高斯过程回归。
- KPLS and KPLSK: 使用PLS降维来处理高维训练数据的KRG变体。
- GPX:是使用 Rust 重新实现的 KRG 和 KPLS,以实现更快的训练/预测操作。
- GEKPLS:利用衍生品训练数据来提高替代模型质量。
- MGP:考虑了定义为密度函数的超参数的不确定性。
- SGP:实现了稀疏方法,允许处理大型训练数据集,因为其他实现的时间复杂度以及训练点数量的内存成本。
下面介绍经典Kriging模型原理及应用案例。
1. Kriging (KRG)
1.1 基本原理
Kriging是一种插值模型,它是已知函数
f
i
(
x
)
f_i({\bf x})
fi(x) 的线性组合,并添加随机过程
Z
(
x
)
Z({\bf x})
Z(x) :
y
^
=
∑
i
=
1
k
β
i
f
i
(
x
)
+
Z
(
x
)
.
\hat{y} = \sum\limits_{i=1}^k\beta_if_i({\bf x})+Z({\bf x}).
y^=i=1∑kβifi(x)+Z(x).
Z
(
x
)
Z({\bf x})
Z(x) 是随机过程的实现,其均值为零,空间协方差函数为:
c
o
v
[
Z
(
x
(
i
)
)
,
Z
(
x
(
j
)
)
]
=
σ
2
R
(
x
(
i
)
,
x
(
j
)
)
cov\left[Z\left({\bf x}^{(i)}\right),Z\left({\bf x}^{(j)}\right)\right] =\sigma^2R\left({\bf x}^{(i)},{\bf x}^{(j)}\right)
cov[Z(x(i)),Z(x(j))]=σ2R(x(i),x(j))
其中
σ
2
\sigma^2
σ2 是过程方差,
R
R
R 是相关性。SMT 中有四种类型的相关性函数。
- 指数相关函数(Exponential correlation function, Ornstein-Uhlenbeck process):
∏ l = 1 n x exp ( − θ l ∣ x l ( i ) − x l ( j ) ∣ ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx}\exp\left(-\theta_l\left|x_l^{(i)}-x_l^{(j)}\right|\right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nxexp(−θl xl(i)−xl(j) ),∀ θl∈R+ - 平方指数(高斯)相关函数(Squared Exponential (Gaussian) correlation function):
∏ l = 1 n x exp ( − θ l ( x l ( i ) − x l ( j ) ) 2 ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx}\exp\left(-\theta_l\left(x_l^{(i)}-x_l^{(j)}\right)^{2}\right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nxexp(−θl(xl(i)−xl(j))2),∀ θl∈R+ - 具有可变幂的指数相关函数(Exponential correlation function with a variable power):
∏ l = 1 n x exp ( − θ l ∣ x l ( i ) − x l ( j ) ∣ p ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx}\exp\left(-\theta_l\left|x_l^{(i)}-x_l^{(j)}\right|^{p}\right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nxexp(−θl xl(i)−xl(j) p),∀ θl∈R+ - Matérn 5/2 相关函数(Matérn 5/2 correlation function):
∏ l = 1 n x ( 1 + 5 θ l ∣ x l ( i ) − x l ( j ) ∣ + 5 3 θ l 2 ( x l ( i ) − x l ( j ) ) 2 ) exp ( − 5 θ l ∣ x l ( i ) − x l ( j ) ∣ ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx} \left(1 + \sqrt{5}\theta_{l}\left|x_l^{(i)}-x_l^{(j)}\right| + \frac{5}{3}\theta_{l}^{2}\left(x_l^{(i)}-x_l^{(j)}\right)^{2}\right) \exp\left(-\sqrt{5}\theta_{l}\left|x_l^{(i)}-x_l^{(j)}\right|\right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nx(1+5θl xl(i)−xl(j) +35θl2(xl(i)−xl(j))2)exp(−5θl xl(i)−xl(j) ),∀ θl∈R+
Matérn 3/2相关函数(Matérn 3/2 correlation function):
∏ l = 1 n x ( 1 + 3 θ l ∣ x l ( i ) − x l ( j ) ∣ ) exp ( − 3 θ l ∣ x l ( i ) − x l ( j ) ∣ ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx} \left(1 + \sqrt{3}\theta_{l}\left|x_l^{(i)}-x_l^{(j)}\right|\right) \exp\left(-\sqrt{3}\theta_{l}\left|x_l^{(i)}-x_l^{(j)}\right|\right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nx(1+3θl xl(i)−xl(j) )exp(−3θl xl(i)−xl(j) ),∀ θl∈R+ - 指数平方正弦相关函数(Exponential Squared Sine correlation function):
∏ l = 1 n x exp ( − θ l 1 ( sin ( θ l 2 ( x l ( i ) − x l ( j ) ) ) 2 ) ) , ∀ θ l ∈ R + \prod\limits_{l=1}^{nx}\exp\left(-\theta_{l_1} \left( \sin \left( \theta_{l_2} \left( x_l^{(i)}-x_l^{(j)} \right)\right)^{2} \right) \right), \quad \forall\ \theta_l\in\mathbb{R}^+ l=1∏nxexp(−θl1(sin(θl2(xl(i)−xl(j)))2)),∀ θl∈R+
这些相关函数由 SMT 中的‘abs_exp’(指数)、‘squar_exp’(高斯)、‘matern52’、‘matern32’和‘squar_sin_exp’调用。
确定性项 ∑ i = 1 k β i f i ( x ) \sum\limits_{i=1}^k\beta_i f_i({\bf x}) i=1∑kβifi(x) 可以替换为常数、线性模型或二次模型。这三种类型在 SMT 中均可用。
在实现中,通过从每个变量(由 X 中的列索引)中减去平均值,然后将每个变量的值除以其标准差来对数据进行规范化:
X
norm
=
X
−
X
mean
X
std
X_{\text{norm}} = \frac{X - X_{\text{mean}}}{X_{\text{std}}}
Xnorm=XstdX−Xmean
有关克里金法的更多详细信息,请参阅 [1].
1.2 使用分类变量或整数变量的Kriging
目的是能够为混合类型变量构建模型。该算法由 Garrido-Merchán 和 Hernández-Lobato 于 2020 年提出[2]。
为了合并整数(具有顺序关系)和分类变量(无顺序),我们使用了连续松弛。对于整数,我们添加一个具有相同界限的连续维度,然后将预测四舍五入为更接近的整数。对于分类,我们添加尽可能多的边界为 [0,1] 的连续维度作为变量的可能输出值,然后我们将预测四舍五入到输出维度,从而给出最大的连续预测。
一种特殊情况是使用 Gower 距离来处理混合整数变量(因此有 gower 核/相关模型选项)。有关此类用法,请参阅 MixedInteger Tutorial。
更多详细信息请参阅 [2]。另请参阅 Mixed integer surrogate。
实施注意事项:混合变量处理适用于所有克里金模型(KRG、KPLS 或 KPLSK),但不能用于导数计算。
2. 案例介绍
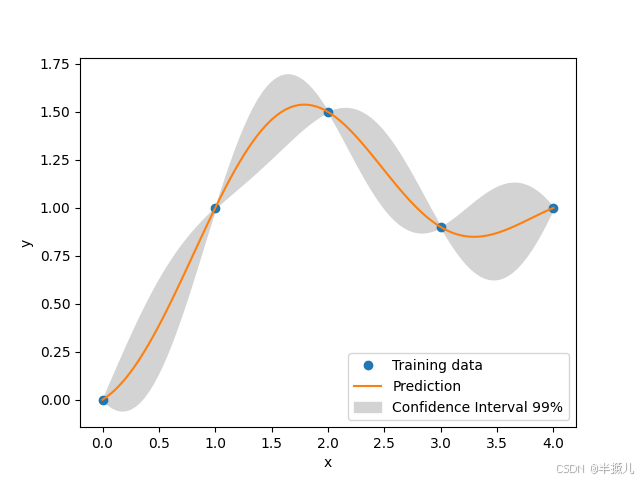
示例1:
# 导入必要的第三方库
import numpy as np
import matplotlib
matplotlib.use('TkAgg') # 用于指定matplotlib使用TkAgg后端进行图形渲染。TkAgg是matplotib的一个后端,它使用Tkinter库来创建图形窗口并显示图表。
import matplotlib.pyplot as plt
from smt.surrogate_models import KRG
# 训练样本点,5个
xt = np.array([0.0, 1.0, 2.0, 3.0, 4.0])
yt = np.array([0.0, 1.0, 1.5, 0.9, 1.0])
# 构造Kriging代理模型
sm = KRG(theta0=[1e-2])
sm.set_training_values(xt, yt)
sm.train()
# 测试样本点(100个)预测
num = 100
x = np.linspace(0.0, 4.0, num)
y = sm.predict_values(x)
# 计算方差
s2 = sm.predict_variances(x)
# 根据第一个变量导数
_dydx = sm.predict_derivatives(xt, 0)
_, axs = plt.subplots(1)
# 带方差绘图
axs.plot(xt, yt, 'o')
axs.plot(x, y)
axs.fill_between(
np.ravel(x),
np.ravel(y - 2.32 * np.sqrt(s2)), # 95% 置信区间为1.96
np.ravel(y + 2.32 * np.sqrt(s2)),
color='lightgrey',
)
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend(
['Training data', 'Prediction', 'Confidence Interval 99%'],
loc = 'lower right'
)
plt.show()
运行结果:
___________________________________________________________________________
Kriging
___________________________________________________________________________
Problem size
# training points. : 5
___________________________________________________________________________
Training
Training ...
Training - done. Time (sec): 0.0690765
___________________________________________________________________________
Evaluation
# eval points. : 100
Predicting ...
Predicting - done. Time (sec): 0.0000000
Prediction time/pt. (sec) : 0.0000000
___________________________________________________________________________
Evaluation
# eval points. : 5
Predicting ...
Predicting - done. Time (sec): 0.0009973
Prediction time/pt. (sec) : 0.0001995
Process finished with exit code 0
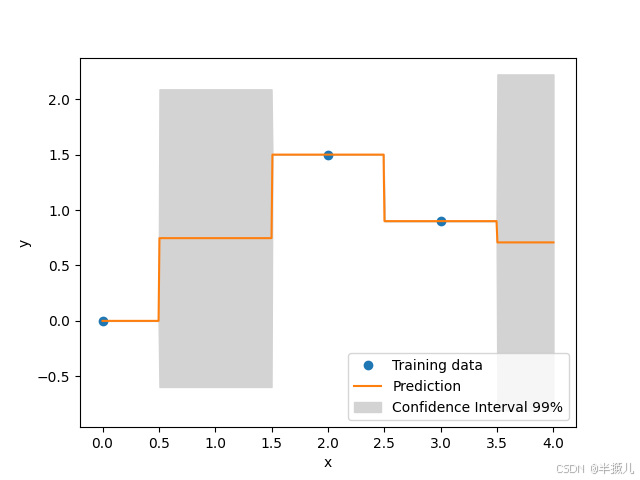
示例2:混合变量类型建模
# 导入必要的第三方库
import numpy as np
import matplotlib
matplotlib.use('TkAgg') # 用于指定matplotlib使用TkAgg后端进行图形渲染。TkAgg是matplotib的一个后端,它使用Tkinter库来创建图形窗口并显示图表。
import matplotlib.pyplot as plt
from smt.surrogate_models import KRG
from smt.applications.mixed_integer import MixedIntegerKrigingModel
from smt.utils.design_space import DesignSpace, IntegerVariable
# 训练样本点,3个
xt = np.array([0.0, 2.0, 3.0])
yt = np.array([0.0, 1.5, 0.9])
design_space = DesignSpace(
[
IntegerVariable(0, 4)
]
)
# 构造Kriging代理模型
sm = MixedIntegerKrigingModel(
surrogate=KRG(design_space=design_space, theta0=[1e-2], hyper_opt='Cobyla')
)
sm.set_training_values(xt, yt)
sm.train()
# 测试样本点(500个)预测
num = 500
x = np.linspace(0.0, 4.0, num)
y = sm.predict_values(x)
# 计算方差
s2 = sm.predict_variances(x)
# 绘图
fig, axs = plt.subplots(1)
axs.plot(xt, yt, 'o')
axs.plot(x, y)
axs.fill_between(
np.ravel(x),
np.ravel(y - 2.32 * np.sqrt(s2)), # 95% 置信区间为1.96
np.ravel(y + 2.32 * np.sqrt(s2)),
color='lightgrey',
)
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend(
['Training data', 'Prediction', 'Confidence Interval 99%'],
loc='lower right'
)
plt.show()
运行结果如下:
___________________________________________________________________________
Evaluation
# eval points. : 500
Predicting ...
Predicting - done. Time (sec): 0.0069811
Prediction time/pt. (sec) : 0.0000140
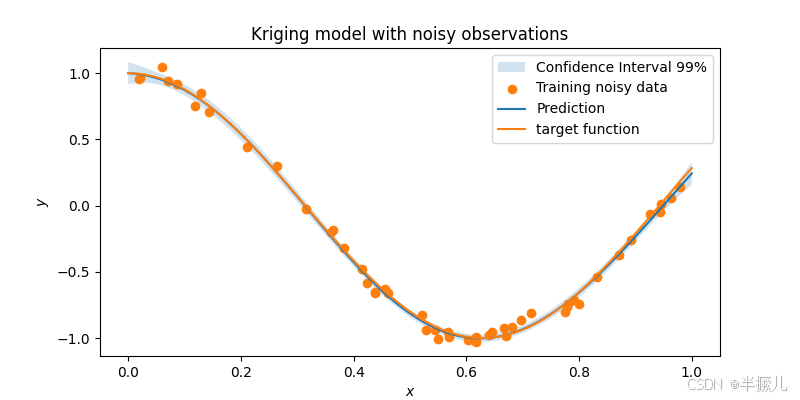
示例3:带噪声数据建模
# 导入必要的第三方库
import numpy as np
import matplotlib
matplotlib.use('TkAgg') # 用于指定matplotlib使用TkAgg后端进行图形渲染。TkAgg是matplotib的一个后端,它使用Tkinter库来创建图形窗口并显示图表。
import matplotlib.pyplot as plt
from smt.surrogate_models import KRG
# 定义一个函数
def target_fun(x):
import numpy as np
return np.cos(5 * x)
# 训练样本点
nobs = 50 # 训练样本点个数
np.random.seed(0) # 可重复性的种子
xt = np.random.uniform(size=nobs)
yt = target_fun(xt) + np.random.normal(scale=0.05, size=nobs) # 在响应输出中添加随机噪声
# 构造Kriging代理模型
sm = KRG(eval_noise=True, hyper_opt='Cobyla')
sm.set_training_values(xt, yt)
sm.train()
# 测试样本点(100个)预测
x = np.linspace(0, 1, 100).reshape(-1, 1)
y = sm.predict_values(x)
# 计算方差
var = sm.predict_variances(x)
# 绘图
plt.rcParams['figure.figsize'] = [8, 4]
plt.fill_between(
np.ravel(x),
np.ravel(y - 2.32 * np.sqrt(var)), # 95% 置信区间为1.96
np.ravel(y + 2.32 * np.sqrt(var)),
alpha=0.2,
label='Confidence Interval 99%'
)
plt.scatter(xt, yt, label='Training noisy data')
plt.plot(x, y, label='Prediction')
plt.plot(x, target_fun(x), label='target function')
plt.title('Kriging model with noisy observations')
plt.legend(loc=0)
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.show()
运行结果如下
___________________________________________________________________________
Kriging
___________________________________________________________________________
Problem size
# training points. : 50
___________________________________________________________________________
Training
Training ...
Training - done. Time (sec): 0.1668217
___________________________________________________________________________
Evaluation
# eval points. : 100
Predicting ...
Predicting - done. Time (sec): 0.0016260
Prediction time/pt. (sec) : 0.0000163
Process finished with exit code 0
参考文献
[1] Sacks, J. and Schiller, S. B. and Welch, W. J., Designs for computer experiments, Technometrics 31 (1) (1989) 41-47.
[2] Garrido-Merchan and D. Hernandez-Lobato, Dealing with categorical and integer-valued variables in Bayesian Optimization with Gaussian processes, Neurocomputing 380 (2020) 20-35.



















