一．写在前面

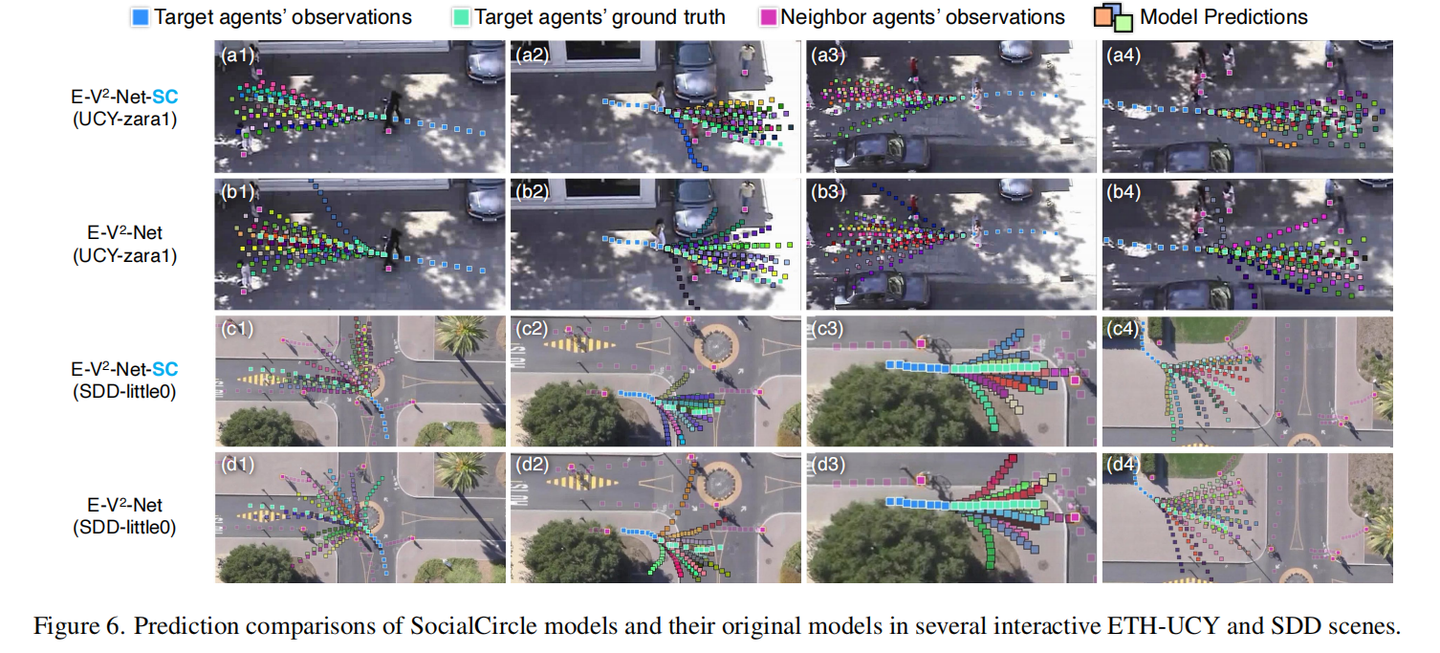
今天要分享的是CVPR 2024上的一篇精彩的行人轨迹预测论文。这篇文章的灵感来源于海洋动物，它们通过回声定位来感知水下同伴的位置。研究者们构建了一种名为 SocialCircle 的全新基于角度的社交互动表示模型，用于动态反映行人相对于目标agent的交互。持续分享领域相关文章，欢迎交流和指正！

参考文献如下：

论文题目：SocialCircle: Learning the Angle-based Social Interaction Representation for Pedestrian Trajectory Prediction

源码地址：

https://github.com/cocoon2wong/SocialCircle​github.com/cocoon2wong/SocialCircle

二. 前言

轨迹预测是自动驾驶等领域的关键任务，要求我们不仅要考虑目标行人的运动，还要理解它们与周围环境和其他行人之间的互动关系。现有方法可以大致分为两类：基于规则的Model-based方法和基于数据驱动的Model-free方法。

• Model-based方法：依赖数学规则进行轨迹预测，通常将其看作是一个优化问题。虽然这些方法在理论上很严谨，但往往缺乏泛化性，难以适用于复杂多变的实际场景。

• Model-free方法：基于数据驱动，尤其是深度学习模型，进行时空交互建模。这类方法的优势在于能够从数据中学习，但由于是“黑盒”模型，可解释性较差。

针对这些问题，本文作者提出了一个结合两者优点的方案——在数据驱动的模型中引入相对简单的社交规则，从而在不损失模型泛化能力的前提下提升可解释性。

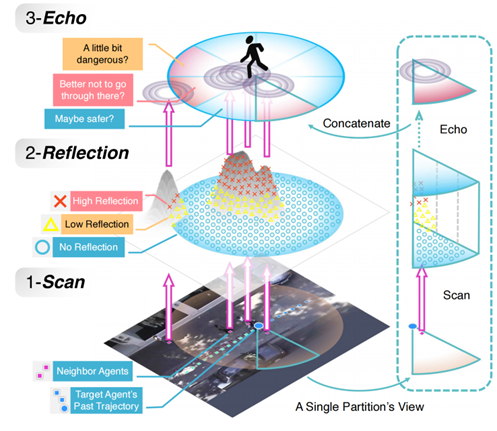
作者还从心理学和仿声学中获得启发：动物在规划路径时，并不是通过复杂的方程求解来分析周围情况，而是通过简单有效的判断来进行行为和交互。比如海洋中的海豚和鲸鱼，它们通过回声定位来感知周围同伴的位置和运动。这启发了作者设计了一个以角度为核心的社交互动建模方法——SocialCircle。

这一现象启发了作者通过回声的方式对交互进行建模。作者们（1）将所有的交互行为映射到一个特殊的空间中，并通过空间角度θ表示这些交互。与此同时，（2）作者采取了全新的序列化建模策略，以时间和轨迹的方式处理和编码空间社交互动。此外，（3）作者提出的方法在多个backbone中进行实验都展现了优异的表现。

三. 相关工作

（此小节方便起见基本都是直接翻译了，对领域了解较多的同学可以跳过）

1. 基于模型的社交互动方法

基于模型的方法旨在使用数学规则作为预测轨迹的基础。 经典的社会力模型[11]被提出来用牛顿力学模拟人类动力学。 佩莱格​​里尼等人。 [34]引入社会力因素来模拟多智能体跟踪任务中的社会行为。 还提出了更多基于社会力的方法，例如[24,29,58]来模拟人群的互动。 在预测轨迹时，还使用其他数学工具和模型来模拟社交互动行为。 谢等人。 [49]提出了“暗物质”模型，用场和基于主体的拉格朗日力学来模拟和预测社会行为。 夏等人。 [48]提出了一种社会转移函数，通过跨多个预测场景的统一方式来模拟人类社会互动行为。 岳等人。 [57]提出了一种神经微分方程模型，其中显式物理模型在建模行人行为时充当强归纳偏差。 然而，这些方法往往难以覆盖所有可能的社交互动案例。 尽管像[48, 57]这样的一些方法利用数据驱动方法的优势来使一些关键参数可训练，但它们仍然可能受到复杂预测场景中复杂数学规则和方程的限制。

2. 无模型的社交互动方法

无模型方法主要通过数据驱动的形式来模拟交互行为。 阿拉希等人 [1]提出了Social Pooling方法来连接附近的序列以相互共享隐藏状态，从而模拟信息共享过程。 提出了像[10, 37]这样的社会池方法的变体，通过同时考虑不同的尺度或位置来池化特征。 像[13]这样的基于网格的方法已经被提出来探索额外的简单规则来增强池化方法的能力。 随着图神经网络的快速发展，图结构已被广泛用于建模社交交互。 图注意力网络（GAT）[23, 32]、图卷积网络[8,39,43]被用来模拟不同节点之间的边的交互。 大多数无模型方法更倾向于更多地关注拟合数据的结构，以便预测的轨迹可以反映社交互动线索的影响。 在这个过程中，很少有直接的数学规则作为约束，使得它们更加依赖于不同的网络结构和高质量的数据。 所提出的 SocialCircle 试图通过向这些可训练的主干引入“精简规则”来解决这些问题，从而利用数据驱动的方法与基于模型的方法的可解释性相结合来建模交互行为。 它还避免了在交互建模过程中设计复杂的数学模型或求解复杂的方程。

三. 方法介绍

1. 问题定义

输入一个交通场景中从第一个时刻到第t_h个时刻的全部agent的位置坐标（p），要求输出它们对应的未来t_f个时刻的轨迹。

2. SocialCircle模型

（1）行人之间的空间关系表示

作者通过角度来表示行人之间的交互关系。首先，将目标行人与周围行人的相对位置用角度表示。作者利用角度 θ_i(j) ∈ [0, 2π) 来表示相邻智能体 j 与目标智能体 i 的相对空间位置。在t_h时刻下，目标行人i 与邻居 j 之间的相对角度可以由公式(1) 定义：

这里的 atan2 是一个函数，利用行人i和邻居j的当前位置信息p^i_{t_h} 和 p^j_{t_h}来计算向量的角度。

（2）SocialCircle的表示（交互表示）

为了方便计算，角度空间[0, 2π]被离散化为多个分区，每个分区对应一个角度范围，并根据这个范围聚合该区域内的交互信息。具体而言，作者将角度空间[0, 2π] 离散为 Nθ个分区，相当于把连续的区间分为若干个离散的部分，这样可以把目标行人i的周围空间按角度划分成多个分区（类似于扇形区域）。目标行人i 的社交圈由分区角度 θ 表示，通过将角度空间 [0, 2π] 离散为Nθ 个分区（其中的每个分区表示了行人 i 周围的一部分空间，这部分空间内的所有邻居都被归类到这个分区中），每个分区对应一个分区函数 f^i（θ_1），其表示目标行人 i 在不同角度范围内的社交交互强度（换而言之，每个分区内聚合邻居的信息）：

这个公式表示的是行人i的“社交圈（SocialCircle）”表示。分区函数实际上就是一个高维的向量序列，表示该分区的交互信息。例如，分区函数f^i（θ_1）则为一个序列化向量，表示的是在被划分到第一个角度分区的所有邻居与目标行人i的交互。（具体的分区函数中各个元素的含义，分区的划分方法，以及分区的序列号方法之后会阐述）

随后，离散分区划分规则如下：

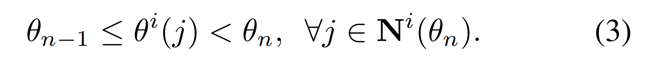
公式(3) 表示分区内选择的邻居满足角度范围的条件，如果邻居j与目标行人i的相对角度满足在第n-1和n个分区之间，那么j邻居就属于分区n

公式(4) 表示邻居数量的约束：

（3）SocialCircle构成

此外每个分区函数f^i包含三个Meta Components：速度（velocity）、距离（distance）和方向（direction），这些成分会被计算并嵌入到高维空间中表示社交互动。目标是通过这些分区的信息来建模行人 i 与周围邻居的交互行为。

此公式说明每个分区函数中所包含的内容

速度 (公式6)：在每个角度分区中，邻居的平均速度由邻居的位移来计算：

距离 (公式7)：通过目标行人i 与邻居的平均欧氏距离来模拟交互的距离因素：

方向 (公式8)：通过计算邻居相对于目标行人的平均角度补偿角度信息丢失的情况：

（4）互动的序列化建模

公式(9) 定义了序列化社交圈的表示方法：

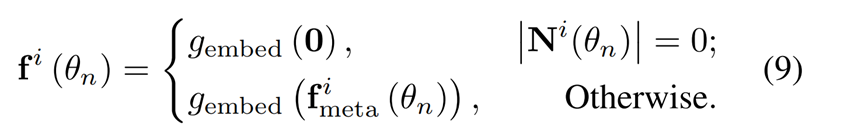
\g_{\text{embed}}在此代表的是包含 2 个全连接层和 64 个输出单元的嵌入函数

此处我们得到的是分区函数，即为序列化后的向量，也称为交互表示。

(5) 填充

通过上述得到交互序列化表示（即分区函数）后，为了使其具有与轨迹数据相同的长度（方便融合），作者将不够的地方则进行填充。也就是作者将空间 SocialCircle视为虚拟时间序列，将交互序列化表示(分区函数)表示为与轨迹 Xi 相同的序列长度（即交互序列化表示=历史轨迹时间长度），以方便后续的模型处理。

社会互动的序列化建模。SocialCircle 被视为“虚拟”时间序列，通过添加零填充与嵌入轨迹共享相同的序列形状，使历史轨迹信息和交互表示可以融合在一起来预测轨迹。

公式(10) 用来处理这些分区序列，使其具有与轨迹数据相同的长度，并通过嵌入函数 g_{\text{embed}}映射到高维空间。

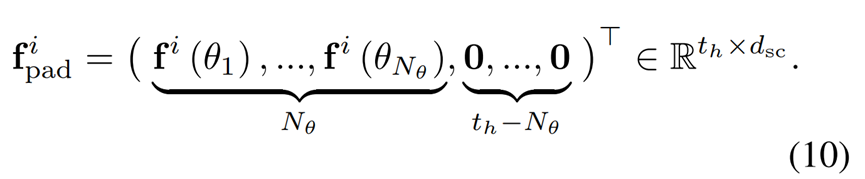
看到这可能有点迷糊，整个过程可以总结为下图：

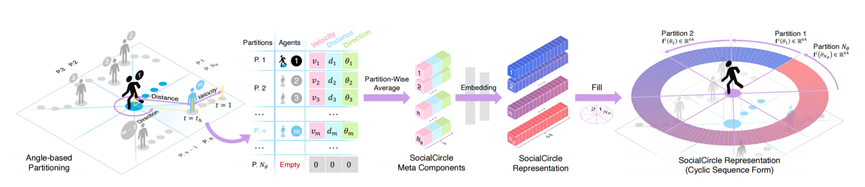
每个agent的交换表示都与其他agent不同。 对于目标agent，它首先计算三个元组件：速度、距离和方向。 然后，这些元组件将在每个基于角度的 SocialCircle 分区内进行平均，最后嵌入到高维头尾循环表示 fi (θn) (1 ≤ n ≤ Nθ) 集合中

具体流程如下：

a. 基于角度的分区（Angle-based Partitioning）： SocialCircle 将目标行人 iii 周围的空间按照角度划分为多个分区，每个分区包含了一些邻居。以图为例，目标行人（编号为1）位于中心，邻居（编号为2、3等）根据它们与目标行人相对位置的不同角度被划分到不同的角度分区中（详见公式2-4）。

b. Meta Components 的计算： 对于每个角度分区 PnP_nPn​，计算三个Meta Components：

• 速度（Velocity）：计算分区内邻居的平均速度。

• 距离（Distance）：计算目标行人 iii 与该分区内邻居之间的平均距离。

• 方向（Direction）：计算邻居相对于目标行人 iii 的平均角度。

这些Meta Components会分别在每个分区计算后取平均值，并生成对应的向量 fi(θn)f^i(\theta_n)fi(θn​)。

c. 嵌入（Embedding）： 将这些Meta Components通过嵌入层映射到高维空间中。这个过程会将每个角度分区的信息转换为高维向量，便于后续的处理（公式9）。

d. 社交圈表示（SocialCircle Representation）： 最终，将所有角度分区的嵌入结果 fi(θn)f^i(\theta_n)fi(θn​) 串联起来，形成一个完整的高维向量序列，这就是行人 iii 的完整社交圈表示，涵盖了其与周围邻居的所有交互信息（公式2）。

e. 序列化和填充： 为了与轨迹预测的时间步长对齐，模型将没有邻居的分区填充为零，并构建一个循环序列表示形式。这使得社交圈表示能够与时间序列的轨迹信息融合，方便后续的时间序列处理和轨迹预测任务（公式10）。

总而言之，通过将目标行人周围的空间按角度划分为多个区域，并计算每个分区中邻居的速度、距离和方向等信息，模型能够生成一个详尽的、嵌入式的社交圈表示，从而为后续的轨迹预测提供更加丰富的交互特征。

3.轨迹预测

作者对比了传统的轨迹预测方法和它们所提出的方法的区别。关键点是在如何处理输入特征，特别是关于目标行人轨迹和社交交互信息的组合方式。

（1）传统的轨迹预测方法

B_{\text{pred}} 是轨迹预测的骨干网络，这种方法将轨迹和社交信息分开处理，分别输入到模型中

传统的轨迹预测模型通常使用骨干网络 B_pred​ 来处理数据，但它们往往将轨迹和社交交互信息分开处理。虽然这种方法可以同时利用这两类信息，但因为是独立处理的，缺乏深度融合，可能会限制模型对这些信息间关系的学习能力，无法完全捕捉它们之间的复杂关联性。

（2）作者提出的方法（SocialCircle Models）

这种方法融合操作将轨迹和社交信息紧密结合

与传统方法不同，SocialCircle 模型通过深度融合目标行人的轨迹信息与其社交交互信息，极大增强了两者之间的相互作用。相比于公式(11)中的传统方法，SocialCircle 模型通过公式(12)中的融合操作，将轨迹和社交信息紧密结合，使得模型能够更好地理解两者的复杂关系。

传统方法与SocialCircle模型的关键区别在于信息的融合方式。SocialCircle模型直接将融合后的向量用于轨迹预测，代替了传统方法中独立输入的社交信息。这种深度融合的方式帮助模型捕捉轨迹与社交互动之间的动态关联性，大大提高了预测的准确性。

这个优化后的轨迹预测模型基于融合后的特征向量，使得模型在预测时可以同时考虑轨迹和社交交互的动态变化。作者提出的SocialCircle Models最大的特点是同时捕捉目标行人的轨迹信息和社交圈中的交互信息，进一步提高预测的准确性。

4.训练

值得注意的是，SocialCircle 模型的训练过程并不需要引入额外的损失函数。相反，它完全可以依赖现有的轨迹预测模型及其骨干网络，如 Transformer、MSN、V²-Net 等，利用它们原有的损失函数来验证模型的性能。在这些现有的深度学习框架下，SocialCircle 模型的交互信息能够被有效学习和优化，从而进一步提升预测精度。

五. 实验

实验部分不再赘述，可以去看原文