文章目录
- 数学概念(全连接层,线性层)
- nn.Linear()
- nn.Parameter()
- Q
- 1. 为什么 self.weight 的权重矩阵 shape 使用 ( out_features , in_features ) (\text{out\_features}, \text{in\_features}) (out_features,in_features)而不是 ( in_features , out_features ) (\text{in\_features}, \text{out\_features}) (in_features,out_features)?
- 2. 为什么是`torch.matmul(x, self.weight.T) + self.bias` 而不是`torch.matmul(self.weight, x) + self.bias`?
- 3. 为什么不直接设置`self.weight = nn.Parameter(torch.randn(input_dim, output_dim))`?
- 计算过程的细分:`torch.matmul()` vs `@` 运算符
- 使用 `F.linear()`
这篇文章会从基础的一个数学概念到对应的代码实现,你将了解到:
- 为什么
nn.Parameter()接受 ( out_features , in_features ) (\text{out\_features}, \text{in\_features}) (out_features,in_features)作为参数?- 为什么不是
torch.matmul(self.weight, x) + self.bias?- 如何使用
torch.matmul(),@或F.linear()去等价地实现nn.Linear()的输出。
数学概念(全连接层,线性层)
线性变化是数学中一个基础的概念,它描述了如何通过线性变换将输入映射到输出。在线性代数中,线性变化通常表示为矩阵乘法。在神经网络中,线性层的核心就是实现这样的矩阵运算。
数学公式:
给定一个输入向量
x
∈
R
n
\mathbf{x} \in \mathbb{R}^n
x∈Rn 和一个输出向量
y
∈
R
m
\mathbf{y} \in \mathbb{R}^m
y∈Rm,线性变化通过矩阵
W
∈
R
m
×
n
\mathbf{W} \in \mathbb{R}^{m \times n}
W∈Rm×n 和偏置项
b
∈
R
m
\mathbf{b} \in \mathbb{R}^m
b∈Rm 进行变换,其公式为:
y
=
W
x
+
b
\mathbf{y} = \mathbf{W} \mathbf{x} + \mathbf{b}
y=Wx+b
- W \mathbf{W} W:是权重矩阵,维度为 m × n m \times n m×n,它决定了输入向量如何线性变换到输出空间;
- x \mathbf{x} x:是输入向量,维度为 n n n,表示特征数据;
- b \mathbf{b} b:是偏置向量,维度为 m m m,用来调整线性变换的输出;
- y \mathbf{y} y:是输出向量,维度为 m m m,是变换后的结果。
例子:
如果输入向量
x
\mathbf{x}
x 有 3 个特征,输出向量
y
\mathbf{y}
y 有 2 个特征,则权重矩阵
W
\mathbf{W}
W 的形状为
2
×
3
2 \times 3
2×3。假设:
W
=
[
1
2
3
4
5
6
]
,
x
=
[
1
2
3
]
,
b
=
[
0
1
]
\mathbf{W} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}
W=[142536],x=
123
,b=[01]
线性变换计算为:
y
=
W
x
+
b
=
[
1
2
3
4
5
6
]
[
1
2
3
]
+
[
0
1
]
=
[
14
32
]
+
[
0
1
]
=
[
14
33
]
\mathbf{y} = \mathbf{W} \mathbf{x} + \mathbf{b} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 14 \\ 32 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 14 \\ 33 \end{bmatrix}
y=Wx+b=[142536]
123
+[01]=[1432]+[01]=[1433]
矩阵运算过程:
[
1
2
3
4
5
6
]
[
1
2
3
]
=
[
(
1
×
1
)
+
(
2
×
2
)
+
(
3
×
3
)
(
4
×
1
)
+
(
5
×
2
)
+
(
6
×
3
)
]
=
[
14
32
]
\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} (1 \times 1) + (2 \times 2) + (3 \times 3) \\ (4 \times 1) + (5 \times 2) + (6 \times 3) \end{bmatrix} = \begin{bmatrix} 14 \\ 32 \end{bmatrix}
[142536]
123
=[(1×1)+(2×2)+(3×3)(4×1)+(5×2)+(6×3)]=[1432]
nn.Linear()
nn.Linear() 会自动创建一个权重矩阵(Weight)和偏置项(Bias),并将它们应用到输入上。
代码示例:
import torch
import torch.nn as nn
# 定义一个输入为3,输出为2的线性层
linear_layer = nn.Linear(3, 2)
# 打印权重矩阵和偏置项
print("权重矩阵 W:")
print(linear_layer.weight)
print("偏置项 b:")
print(linear_layer.bias)
# 模拟输入向量
input_vector = torch.tensor([1.0, 2.0, 3.0])
output_vector = linear_layer(input_vector)
print("输出向量 y:")
print(output_vector)
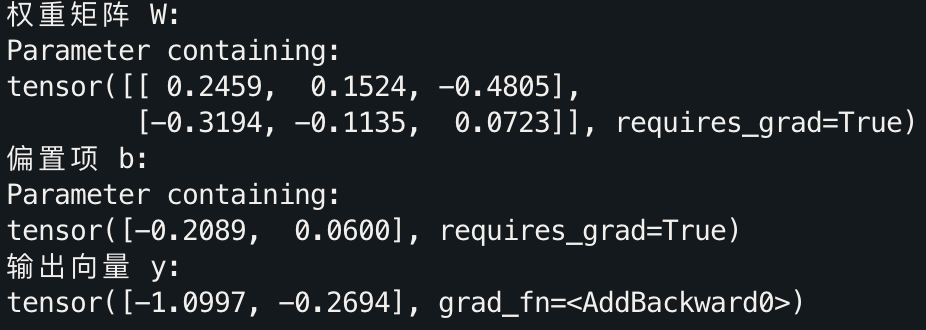
在这里,nn.Linear(3, 2) 创建了一个 2×3 的权重矩阵和一个 2 维的偏置向量。通过 linear_layer(input_vector),可以直接获得输入向量经过线性变换后的输出。
nn.Parameter()
在 PyTorch 中,nn.Linear() 自动处理了权重和偏置项的初始化和更新,但有时你可能希望对这些参数自定义一些操作,比如 LoRA。这时,我们可以使用 nn.Parameter() 来自定义权重和偏置,其实 nn.Linear() 本身就是使用的nn.Parameter(),感兴趣的话可以看官方源码。
以自定义线性层为例:
class CustomLinearLayer(nn.Module):
def __init__(self, input_dim, output_dim):
super(CustomLinearLayer, self).__init__()
# 使用 nn.Parameter 手动定义权重和偏置
self.weight = nn.Parameter(torch.randn(output_dim, input_dim))
self.bias = nn.Parameter(torch.randn(output_dim))
def forward(self, x):
# 手动实现线性变换 y = Wx + b
return torch.matmul(x, self.weight.T) + self.bias
# 使用自定义的线性层
custom_layer = CustomLinearLayer(3, 2)
output = custom_layer(input_vector)
print(output)

在看完代码后,你可能会产生两个疑惑:
Q
1. 为什么 self.weight 的权重矩阵 shape 使用 ( out_features , in_features ) (\text{out\_features}, \text{in\_features}) (out_features,in_features)而不是 ( in_features , out_features ) (\text{in\_features}, \text{out\_features}) (in_features,out_features)?
实际这正是我写这篇博客分享的原因,现在进入正题,因为这个疑惑完全不应该产生。
让我们重新使用 in_features \text{in\_features} in_features和 out_features \text{out\_features} out_features来重现之前的数学定义:
对于输入向量 x ∈ R in_features \mathbf{x} \in \mathbb{R}^{\text{in\_features}} x∈Rin_features,全连接层的输出为:
y = W x + b \mathbf{y} = W\mathbf{x} + \mathbf{b} y=Wx+b
其中:
- W ∈ R out_features × in_features W \in \mathbb{R}^{\text{out\_features} \times \text{in\_features}} W∈Rout_features×in_features 是权重矩阵,
- b ∈ R out_features \mathbf{b} \in \mathbb{R}^{\text{out\_features}} b∈Rout_features 是偏置项。
在线性变换中,输入向量 x \mathbf{x} x 的维度是 in_features \text{in\_features} in_features,而输出向量 y \mathbf{y} y 的维度是 out_features \text{out\_features} out_features。根据矩阵乘法的规则,要将输入 x \mathbf{x} x 映射到输出 y \mathbf{y} y,权重矩阵 W W W 的形状应该是 ( out_features , in_features ) (\text{out\_features}, \text{in\_features}) (out_features,in_features),因为矩阵乘法中 W x W\mathbf{x} Wx的维度要求是:
( out_features × in_features ) × ( in_features × 1 ) = ( out_features × 1 ) (\text{out\_features} \times \text{in\_features}) \times (\text{in\_features} \times 1) = (\text{out\_features} \times 1) (out_features×in_features)×(in_features×1)=(out_features×1)
这保证了输出 y \mathbf{y} y 的维度是 out_features \text{out\_features} out_features。
如果权重矩阵的形状是 ( in_features , out_features ) (\text{in\_features}, \text{out\_features}) (in_features,out_features),矩阵乘法的维度将不匹配,无法实现线性变换。
现在是不是感觉清晰了?不要 nn.Linear(in_feature, out_feature) 用多了就将权重矩阵当作是
(
in_features
,
out_features
)
(\text{in\_features}, \text{out\_features})
(in_features,out_features)遗忘了线性代数的概念,数学才是这一切的基石。
2. 为什么是torch.matmul(x, self.weight.T) + self.bias 而不是torch.matmul(self.weight, x) + self.bias?
主要原因还是在于 输入张量 x 的形状 和 矩阵乘法规则。
一般来说,模型的输入 x 实际上并不是
(
in_features
,
1
)
(\text{in\_features}, 1)
(in_features,1),而是
(
batch_size
,
in_features
)
(\text{batch\_size}, \text{in\_features})
(batch_size,in_features),而权重矩阵 self.weight 的形状是
(
out_features
,
in_features
)
(\text{out\_features}, \text{in\_features})
(out_features,in_features),我们需要实现的线性变换是:
y
=
W
x
+
b
y = W x + b
y=Wx+b
根据矩阵乘法规则,第一个矩阵的列数必须等于第二个矩阵的行数,这意味着我们不能直接计算 torch.matmul(self.weight, x),因为这样会导致维度不匹配:
self.weight形状为 ( out_features , in_features ) (\text{out\_features}, \text{in\_features}) (out_features,in_features),x形状为 ( batch_size , in_features ) (\text{batch\_size}, \text{in\_features}) (batch_size,in_features)。torch.matmul(self.weight, x)的维度计算规则将要求x的形状为 ( in_features , batch_size ) (\text{in\_features}, \text{batch\_size}) (in_features,batch_size),但这与模型的输入不匹配。
因此,正确的矩阵乘法应该是 torch.matmul(x, self.weight.T),其中 self.weight.T 表示 self.weight 的转置矩阵,此时的形状为
(
in_features
,
out_features
)
(\text{in\_features}, \text{out\_features})
(in_features,out_features)。
这样,torch.matmul(x, self.weight.T) 的维度计算为:
( batch_size , in_features ) × ( in_features , out_features ) = ( batch_size , out_features ) (\text{batch\_size}, \text{in\_features}) \times (\text{in\_features}, \text{out\_features}) = (\text{batch\_size}, \text{out\_features}) (batch_size,in_features)×(in_features,out_features)=(batch_size,out_features)
这就得到了正确的输出形状 ( batch_size , in_features ) (\text{batch\_size}, \text{in\_features}) (batch_size,in_features)。
3. 为什么不直接设置self.weight = nn.Parameter(torch.randn(input_dim, output_dim))?
这样不就可以不转置直接使用torch.matmul(x, self.weight)了吗?的确如此,或许是因为
(
out_features
,
in_features
)
(\text{out\_features}, \text{in\_features})
(out_features,in_features) 对于矩阵运算
W
x
W\mathbf{x}
Wx 来讲更符合直觉吧。
计算过程的细分:torch.matmul() vs @ 运算符
在 PyTorch 中,torch.matmul() 用于实现矩阵乘法,而 @ 是其简洁的符号形式,是 Python 的语法糖,二者在功能上是等价的。
示例代码:
import torch
# 定义权重矩阵 W 和输入向量 input_vector
W = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
input_vector = torch.tensor([1.0, 2.0, 3.0])
# 使用 torch.matmul 实现矩阵乘法
result1 = torch.matmul(W, input_vector)
# 使用 @ 运算符
result2 = W @ input_vector
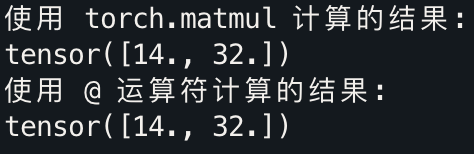
print("使用 torch.matmul 计算的结果:")
print(result1)
print("使用 @ 运算符计算的结果:")
print(result2)
结果:
使用 F.linear()
PyTorch 提供了 F.linear() 作为函数式接口,它与 nn.Linear() 类似,但不需要创建一个线性层对象。F.linear() 可以接受线性层的权重和偏置作为输入,在下一篇有关 LoRA 的文章中,你将看到使用范例。
示例代码:
import torch.nn.functional as F
# 使用 F.linear 进行线性变换
output = F.linear(input_vector, linear_layer.weight, linear_layer.bias)
print(output)