Shading着色

冯氏光照 / Blinn-Phong着色模型：

环境光（常量）：颜色 * 强度

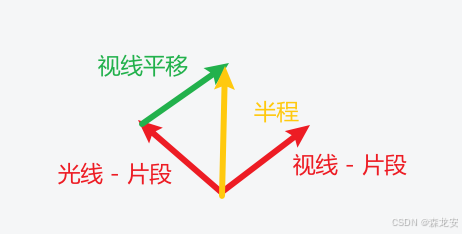
法线n，观测方向v，光照方向I，反射光线R，半程向量H（V和I的角平分线）光泽度shininess，自身颜色color

//

两个性质：

能量守恒（决定到达的能量）：

1. 光的传播过程中，总能量保持不变，反射的能量不能超过入射的能量
2. 入射光的能量等于反射光和折射光的总能量

余弦定理（决定接受的能量）：I与n夹角越大，物体表面接受的光照总量越小，即点乘结果

漫反射：kd为本身的颜色 * 到达能量 * 吸收的比率

//

R和V夹角越近，颜色强度越大，等价于，H和n的夹角

半程向量 = I + V / || I + V || 归一化（仅方向）

指数p：比如没有指数，在比如45的角度下看平面，会看到比较大的高光区域，因为cos值仍比较大，因为对于很多点都有比较亮的高光

镜面：ks为高光的颜色（通常为白色） * 到达能量 * 看到高光的比率，指数p（通常为100~200）

插值

问题：  即使只为平面传入了4个顶点，片段着色器依然能够正确地为整个平面的每个像素（片段）计算光照和颜色？

这是因为进行了线性插值：已知数据点之间估算中间数据值的过程，插值的目的是通过已知顶点的属性，计算出多边形内部任意位置的属性值。

插值的不同类型

1. 线性插值：这是最常见的方式。在顶点之间进行线性插值，得到内部片段的属性。它根据片段距离每个顶点的比例来插值数据。

2. 重心插值：这是光栅化过程中使用的一种特殊插值方法。重心插值通过三角形的重心坐标（barycentric coordinates），根据片段相对于每个顶点的重心坐标

3. 透视校正插值：在3D场景中，由于透视投影的存在，单纯的线性插值可能导致错误的结果。因此，OpenGL会使用透视校正插值，确保在透视投影下的正确性。

理解框架中插值：

l​​​​​这篇计算插值的方式讲的很清楚可以看到，对于普通的线性插值，和权重有关，

对于例如三角形内部重心插值，和三角形面积有关

注意如何求每个三角形面积，根据叉乘，首先求出平行四边形面积（两个向量叉乘的结果） / 2= 三角形面积

如下computeBarycentric2D函数计算点（x，y）在三角形被3个顶点v0v1v2，影响的权重比（对应3个三角形面积 / 总面积），也就是求出3个面积 / 总面积即可

最后利用abg的3个权重值，计算采样点的z深度值

//计算坐标在三角形的重心坐标
static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector3f* v)
{
    float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) /
     (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y());
    float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) /
     (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y());
    float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) /
     (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y());
    return {c1,c2,c3};
}
// 
std::tie(alpha, beta, gamma) = computeBarycentric2D(i+a[k], j+a[k+1], t.v);//重心插值
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());//透视校正
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;//得到校正后的深度z值

3种着色方式： 

Face Flat平面着色：对每个三角形四边形有相同的法线，法线根据三角形边两个两个插值得到，因此每个三角形内部有完全一致的结果

Vertex Gouraud顶点着色：对每个顶点着色，内部用插值计算颜色，结果近似

Pixel Phong像素着色：着色应用在每个像素上，法线方向在内部插值，有更精确的结果

//

这里如何求法线平均？

比如某顶点是周围三角形的公有顶点，求这个顶点的法线，就是其他的三角形法线方向的加权平均值

渲染流水线

渲染流水线：将 3D 场景 转换为 2D 图像的过程

• 渲染流水线（Rendering Pipeline）：侧重于 GPU 内部的处理阶段，尤其是渲染的各个阶段如何协作从 3D 数据生成图像。更具技术细节，描述数据如何在 GPU 上流动。

• 渲染管线（Render Pipeline）：是一个更宽泛的概念，涵盖了从场景数据组织到图形渲染的全流程，包括 CPU 端的场景管理、资源调度、API 调用以及 GPU 的流水线处理。

• 图形管线（Graphics Pipeline）：主要描述图形 API（如 OpenGL、Vulkan 等）如何控制 GPU 渲染阶段。更注重图形 API 的设计和其对 GPU 的控制流程。

Shader：是渲染流水线中可编程的部分，

和作业框架不同，使用图形api时，对于顶点或片段的操作应写在shader中，对于opengl来说需要用glsl语言，directx需要hlsl语言……

当bind绑定shader并调用drawcall时，会自动（非for循环）对每个顶点计算位置和片段/像素计算颜色，运行绑定的着色器

• 顶点着色器（Vertex Shader）：处理每个顶点的输入，计算坐标变换、法线变换、纹理坐标等。

• 片段着色器（Fragment Shader）：处理光栅化后每个像素（片段）的颜色、纹理映射、光照计算等。

• 几何着色器（Geometry Shader）：可选阶段，用于在顶点之后、光栅化之前对几何体进行修改。

• 计算着色器（Compute Shader）：独立于渲染流水线，可以用于并行处理复杂计算任务，比如物理模拟、流体模拟等。

GPU：执行渲染流水线，并以极高的效率并行执行流水线中的任务。