大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述:
两个线段获得的最多奖品
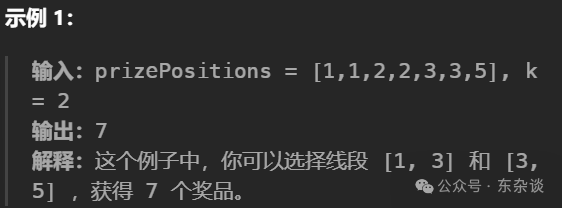
在 X轴 上有一些奖品。给你一个整数数组 prizePositions ,它按照 非递减 顺序排列,其中 prizePositions[i] 是第 i 件奖品的位置。数轴上一个位置可能会有多件奖品。再给你一个整数 k 。
你可以同时选择两个端点为整数的线段。每个线段的长度都必须是 k 。你可以获得位置在任一线段上的所有奖品(包括线段的两个端点)。注意,两个线段可能会有相交。
比方说 k = 2 ,你可以选择线段 [1, 3] 和 [2, 4] ,你可以获得满足 1 <= prizePositions[i] <= 3 或者 2 <= prizePositions[i] <= 4 的所有奖品 i 。
请你返回在选择两个最优线段的前提下,可以获得的最多奖品数目。

解题思路:
这是一个典型的动态规划问题,通过巧妙的划分和二分查找我们可以高效地解决。
有一个非递减排列的奖品位置数组 prizePositions(第i个奖品的位置在prizePositions[i]),及一个整数 k 表示线段的长度。目标是选择两个长度为 k 的线段,以尽可能覆盖更多的奖品位置。每个线段可以覆盖其起始点到其起始点加上 k 的范围内的奖品,两个线段之间可以重叠,但理想情况下,重叠部分应该最小化,从而增强覆盖数量。
使用动态规划(DP)数组 dp 来存储到每个位置的最大奖品覆盖数,利用二分查找来加快寻找线段覆盖边界的过程。
先写一个最基础的二分查找函数
int lower_bound(int* arr, int size, int val) {int low = 0, high = size;while (low < high) {int mid = (low + high) / 2;if (arr[mid] < val) {low = mid + 1;} else {high = mid;}}return low;}//这个函数实现了二分查找,目的是寻找在给定的排序数组 arr 中//第一个不小于 val 的元素的索引。
随后我们进行设计用于计算所能得到的最大奖品数量的函数
int maximizeWin(int* prizePositions, int prizePositionsSize, int k) {int* dp = (int*)calloc(prizePositionsSize + 1, sizeof(int));int ans = 0;for (int i = 0; i < prizePositionsSize; i++) {// 查找小于 prizePositions[i] - k 的最右侧位置int x = lower_bound(prizePositions, prizePositionsSize, prizePositions[i] - k);// 更新最大奖品数量ans = fmax(ans, i - x + 1 + dp[x]);// 更新 dp 数组,dp[i + 1] 记录到达 i 的最佳覆盖数量dp[i + 1] = fmax(dp[i], i - x + 1);}free(dp); // 释放分配的内存return ans; // 返回最大奖品数量}
解析步骤:
-
初始化:
-
dp 数组用于存储状态。
-
ans 变量用于记录全局最大奖品数量。
-
-
循环:
-
遍历每一个位置 i,代表第二条线段的右端点。
-
使用 lower_bound 函数查找当前奖品位置 prizePositions[i] 左侧的界限 prizePositions[i] - k 对应的 j 值。
-
-
更新最大奖品数量:
-
通过 ans = fmax(ans, i - x + 1 + dp[x]),从当前 i 计算出第二条线段覆盖的数量 i - x + 1 加上第一条线段的贡献 dp[x]。
-
这里,i - x + 1 表示第二条线段覆盖的奖品数量,dp[x] 则表示第一条线段在 prizePositions[j - 1] 之前的最优覆盖。
-
-
更新 dp 数组:
-
使用 dp[i + 1] = fmax(dp[i], i - x + 1) 更新 dp 数组,确保 dp[i + 1] 是到目前为止所能覆盖的最大奖品数量。
-
-
内存释放和返回值:
-
最后释放 dp 数组的内存,返回最终的最大奖品数量 ans。
-
时间复杂度:
-
时间复杂度: O(n log n)
-
外层循环遍历 prizePositionsSize 需 O(n)。
-
在每次循环中,二分查找的时间复杂度为 O(log n)。
-
空间复杂度:
-
空间复杂度: O(n)
-
需要 dp 数组,大小为 prizePositionsSize + 1。
-