【FPGA数字信号处理】- FIR串行滤波器

news2024/9/20 16:39:43

理解和掌握 FIR 串行滤波器是踏入数字信号处理领域的重要一步。

那么，什么是 FIR 串行滤波器？它是如何工作的？又有着怎样的神奇之处呢？让我们一起揭开它的神秘面纱。

一、FIR 滤波器简介

FIR 滤波器，全称为有限脉冲响应（Finite Impulse Response）滤波器，是数字信号处理系统中最基本的元件之一。

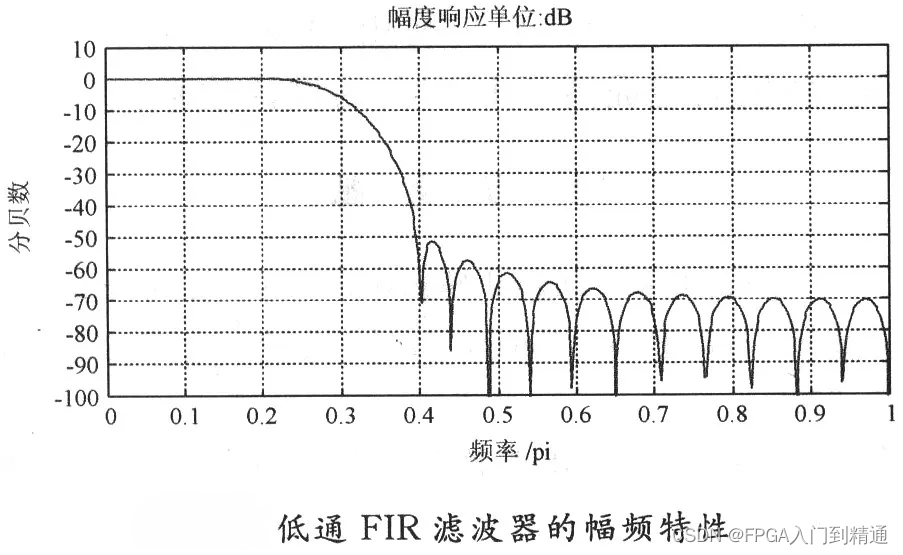
与其他滤波器相比，FIR 滤波器具有独特的优势。它可以在保证任意幅频特性的同时具有严格的线性相频特征，这意味着它能够在对信号进行滤波处理时，不会对信号的相位产生扭曲，从而保证了信号的准确性。

此外，FIR 滤波器的单位抽样响应是有限长的，这使得滤波器是稳定的系统，不会像某些无限脉冲响应滤波器那样可能出现不稳定的情况。

二、FIR滤波器的工作原理

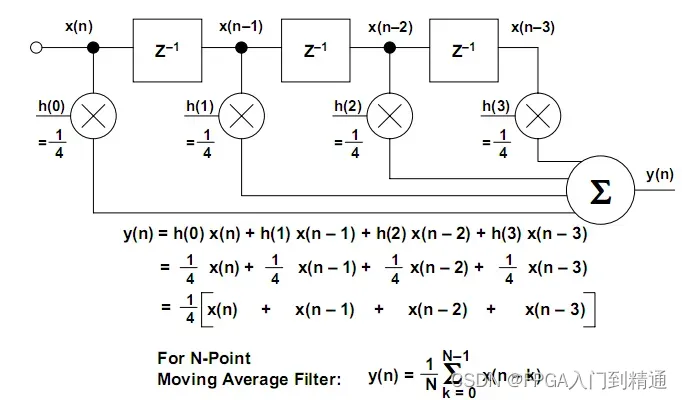
FIR滤波器的核心在于输入信号与单位冲击响应函数的卷积运算。

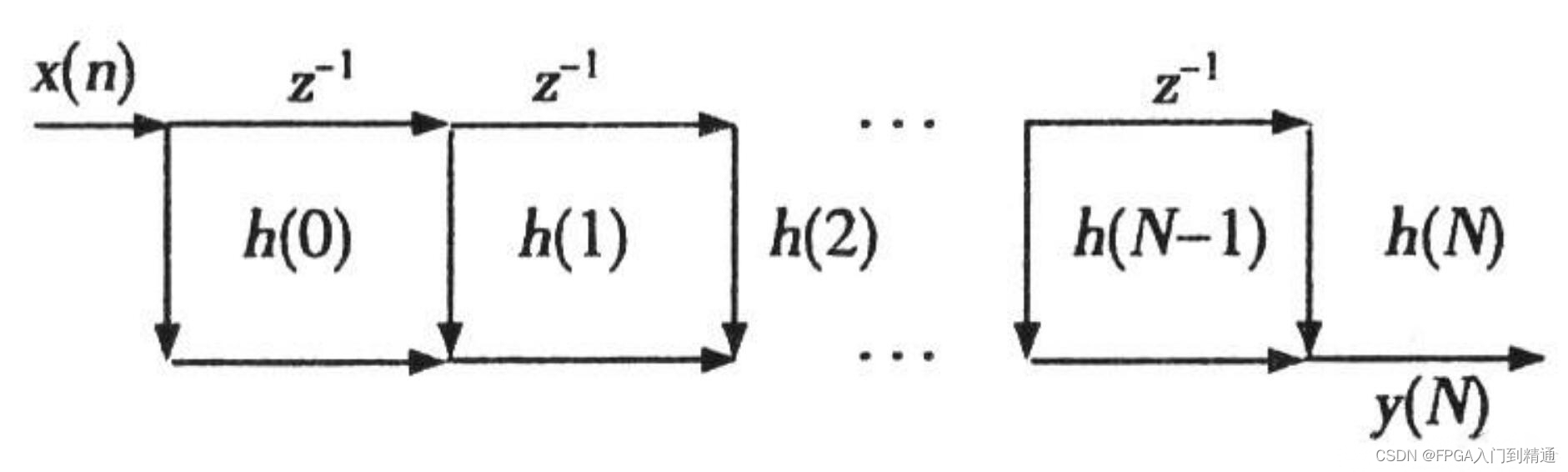
简单来说，就是将输入信号与滤波器的系数进行逐点相乘，然后将乘积结果累加起来，得到输出信号。

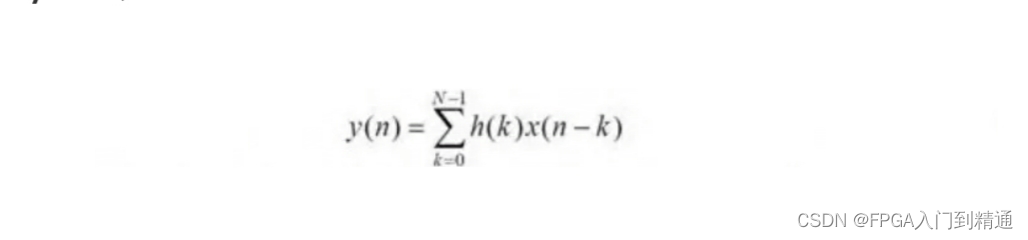
在并行结构中，同一个时刻，每个输入数据都与对应的滤波器系数相乘，并同时将上一个时刻各项乘法的结果进行求和，这样就能得到滤波结果，每个周期输出一个数据，也就是说滤波计算处理频率与输入信号采样频率一样，但消耗的资源会随着滤波器阶数而增加。

在串行结构中，只需要一个乘法器即可，可以节省资源，为了满足输入信号采样频率下同步输出滤波结果，也就是在一个输入信号周期内，需要完成所有计算，所以对于一个N阶FIR滤波器，考虑到对称系数的特性只要做N/2个乘法运算，也就是计算处理频率是输入信号采样频率的N/2倍。

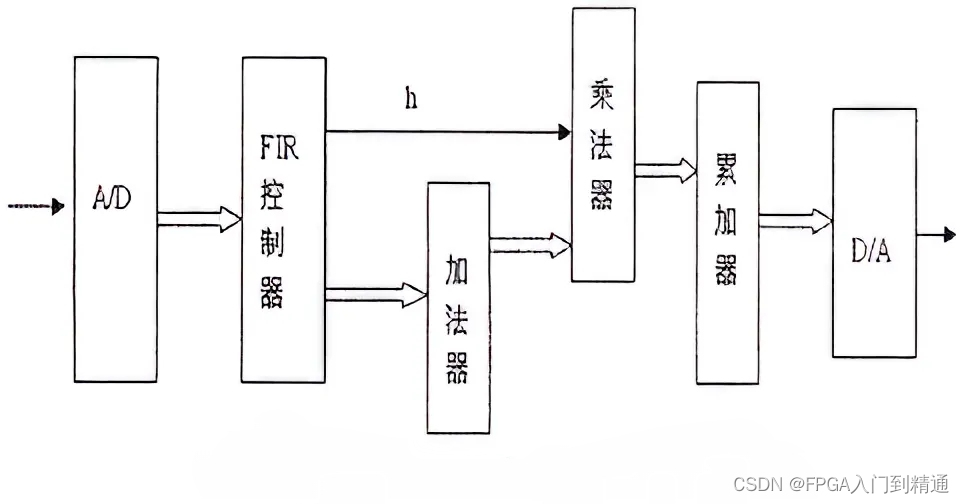
三、FPGA代码实现

module fir_serial
(
input rst,
input clk,
input [11:0] data_in,
output [28:0] data_out
);

reg [12:0] add_a, add_b;
wire [12:0] add_s;

reg [11:0] coe; //12bit量化滤波器系数
wire [24:0] Mout;

reg [2:0] cnt;
reg [11:0] data_reg[15:0];
integer i;

reg [28:0] sum;
reg [28:0] data_out_temp;

always @ (posedge clk or posedge rst)
if (rst) cnt <= 'd0;
else cnt <= cnt + 1'b1;

always @ (posedge clk or posedge rst)
if (rst) begin //清0
data_reg[15] <= 'd0;
for (i=0; i<15; i=i+1'b1)
data_reg[i] <= 'd0;
end else begin
if (cnt == 'd7) begin
for (i=0; i<15; i=i+1'b1) //移位
data_reg[i+1] <= data_reg[i];
data_reg[0] <= data_in;
end
end

always @ (posedge clk or posedge rst)
if (rst) begin
add_a <= 'd0; add_b <= 'd0; coe <= 'd0;
end
else begin
case (cnt)
'd0: begin
add_a <= {data_reg[0][11], data_reg[0]};
add_b <= {data_reg[15][11], data_reg[15]};
coe <= 12'h000;
end
'd1: begin
add_a <= {data_reg[1][11], data_reg[1]};
add_b <= {data_reg[14][11], data_reg[14]};
coe <= 12'hffd;
end
'd2: begin
add_a <= {data_reg[2][11], data_reg[2]};
add_b <= {data_reg[13][11], data_reg[13]};
coe <= 12'h00f;
end
default: begin //第四个周期
add_a <= {data_reg[3][11], data_reg[3]};
add_b <= {data_reg[12][11], data_reg[12]};
coe <= 12'h02e;
end
endcase
end

assign add_s = add_a + add_b;
mult_gen_0 mult_inst
(
.CLK (clk),
.A (coe),
.B (add_s),
.P (Mout)
);
always @ (posedge clk or posedge rst)
if (rst) begin
sum <= 'd0; data_out_temp <= 'd0;
end
else begin
if (cnt == 'd2) begin
data_out_temp <= sum; sum <= {{4{Mout[24]}}, Mout};
end else
sum <= sum + {{4{Mout[24]}}, Mout};
end

assign data_out = data_out_temp;
endmodule