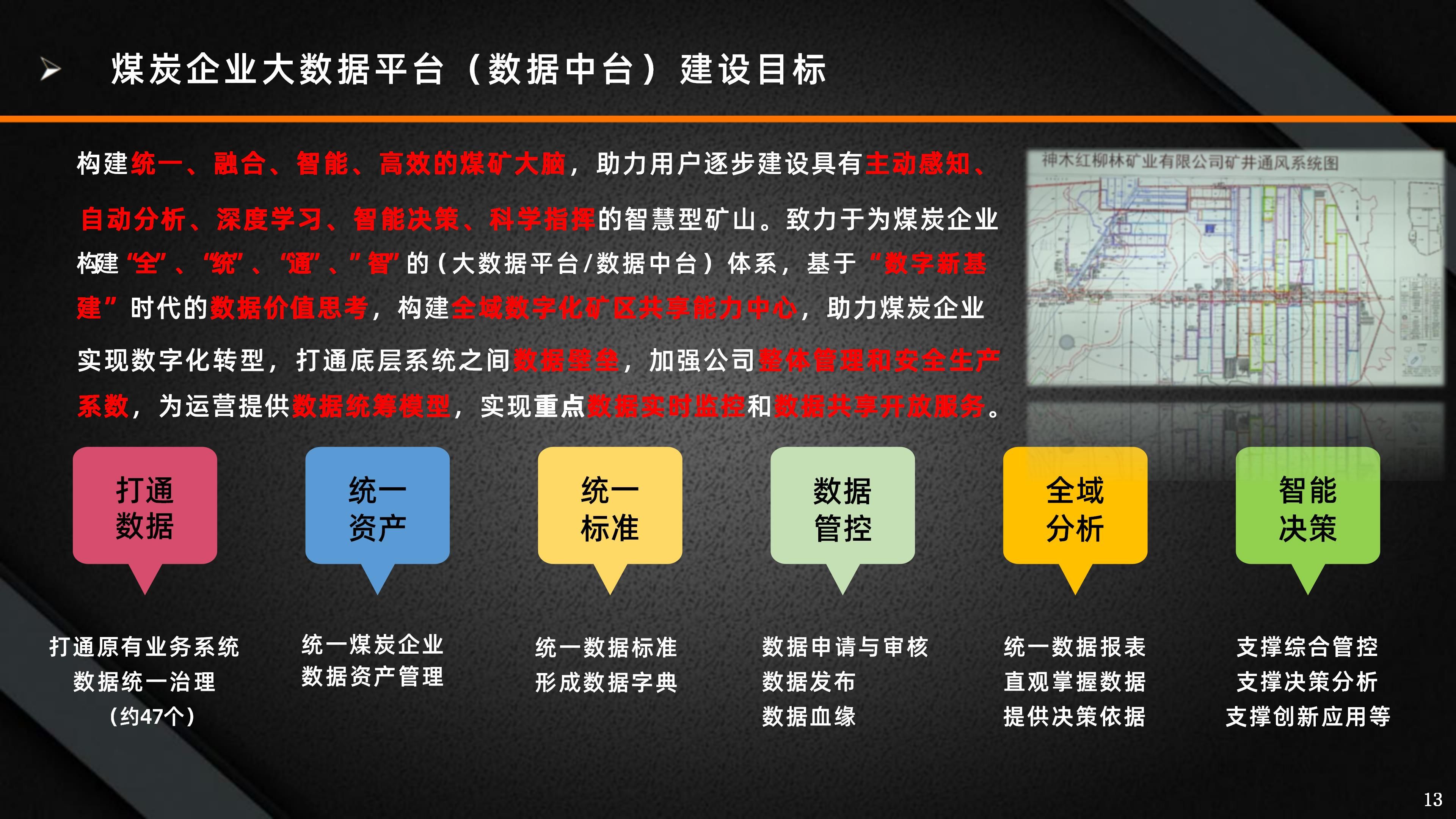
设计新的多目标测试函数时,需要考虑多个因素以确保它们能够有效地评估和比较多目标优化算法。以下是一些常见的设计原则和考虑因素:
-
目标函数的多样性:测试函数应涵盖不同类型的目标函数,如线性、非线性、凸函数、凹函数等,以测试算法在不同情况下的表现。
-
解空间的复杂性:设计的目标函数应具有不同的解空间复杂性,包括多模态性(多个局部最优解)、非凸性、高维性等。
-
帕累托前沿的形状:帕累托前沿是多目标优化中的关键概念,它表示了所有非劣解的集合。测试函数应具有不同的帕累托前沿形状,如线性、非线性、离散、连续等。
-
约束条件:测试函数可能包含各种类型的约束,包括线性约束、非线性约束、等式约束和不等式约束。这些约束应具有不同的难度和复杂性。
-
可扩展性:测试函数应能够轻松扩展到不同数量的目标和变量,以测试算法在不同规模问题上的表现。
-
参数的可控性:测试函数应允许调整参数以改变其难度和特性,这有助于研究者系统地分析算法的性能。
-
全局和局部最优解:测试函数应具有明确的全局最优解和局部最优解,以便于评估算法的收敛性和搜索能力。
-
解的分布:解空间中的解应均匀分布,以测试算法在不同区域的搜索能力。
-
计算成本:测试函数的计算成本应适中,以确保算法可以在合理的时间内评估。
-
可重复性:测试函数应具有明确的数学定义和实现方式,以确保不同研究者和算法可以在相同的条件下进行比较。
-
可视化:测试函数应易于可视化,这有助于直观地理解问题和算法的行为。
-
基准解集:对于测试函数,最好有一个已知的基准解集,这有助于评估算法的性能和收敛性。
-
文献支持:测试函数应有文献支持,说明其设计原理和应用背景,以增加其可信度和实用性。
-
公平性:测试函数应公平地评估所有算法,不应偏向于特定类型的算法。
通过考虑这些原则和因素,研究者可以设计出能够有效评估多目标优化算法性能的测试函数。
参考文献: Zhang Q , Zhou A , Zhao S , et al. Multiobjective optimization Test Instances for the CEC 2009 Special Session and Competition[J]. Mechanical engineering (New York, N.Y.: 1919), 2008.

CEC2009中无约束多目标测试集(UF1-UF10)详情如下: