375. 猜数字大小II

题目分析

题目链接：375. 猜数字大小 II - 力扣（LeetCode）

题目比较长，大致意思就是给一个数，比如说10，定的数字是7，让我们在[1, 10]这个区间猜。

如果猜大或猜小都会说明是大了还是小了，此外，我们还需要支付猜错数字对应的现金。

现在就是让我们定制一个猜测策略，确保准备最少的钱能猜对

如果采用二分查找，只能确保最小次数，题目要求的是最小金额

算法原理

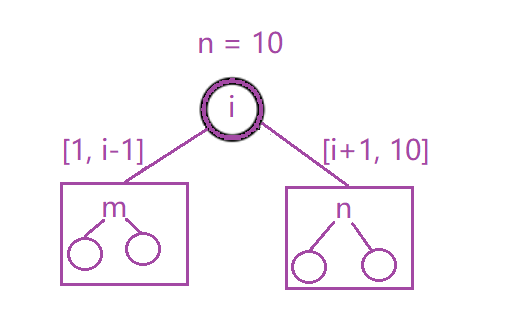
随便选一个数i最为起始位置，如果不对就进入往下找：

1. 选小了：[1, i-1]
2. 选大了：[i+1,10]

从这里面继续选一个数作为“根节点”，这就出现了重复情况了：

• 给一个区间，选一个头，在左右子树里面找出最小值

当以i为根节点的时候，左右子树返回的值，选择较大值，因为确保在整个操作当中，都是完胜的。

代码实现

暴搜：

会超时

class Solution {
public:
    int getMoneyAmount(int n)
    {
        return dfs(1, n);
    }

    int dfs(int left, int right)
    {
        //left > right 此时区间不合法，选不出来
        //left == right 到叶子节点了，就是要选择的，选对不用支付
        if(left >= right)
        {
            return 0;
        }
        int ret = INT_MAX;
        for(int i = left; i <= right; i++)
        {
            int l = dfs(left, i-1);
            int r = dfs(i+1, right);
            ret = min(ret, i+max(l, r));
        }
        return ret;
    }
};

记忆化搜索：

出现重复情况，可采用记忆化搜索

class Solution {
public:
    int memo[201][201];
    int getMoneyAmount(int n)
    {
        return dfs(1, n);
    }

    int dfs(int left, int right)
    {
        //left > right 此时区间不合法，选不出来
        //left == right 到叶子节点了，就是要选择的，选对不用支付
        if(left >= right)
        {
            return 0;
        }
        if(memo[left][right] != 0)
        {
            return memo[left][right];
        }
        int ret = INT_MAX;
        for(int i = left; i <= right; i++)
        {
            int l = dfs(left, i-1);
            int r = dfs(i+1, right);
            ret = min(ret, i+max(l, r));
        }
        memo[left][right] = ret;
        return ret;
    }
};

329. 矩阵中的最长递增路径

题目链接：329. 矩阵中的最长递增路径

题目较短，就不分析了

算法原理

找个一个位置，上下左右开始试，如果有递增的，则走到下一个节点，然后又开始上下左右尝试，记录最长的情况

代码实现

暴搜会超时，记忆化搜索加一个备忘录即可

class Solution {
public:
    int memo[201][201];
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    vector<vector<int>> matrix;
    int m, n;
    int longestIncreasingPath(vector<vector<int>>& _matrix)
    {
        matrix = _matrix;
        int ret = 0;
        m = matrix.size();
        n = matrix[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                ret = max(ret, dfs(i, j));
            }
        }
        return ret;
    }

    int dfs(int i, int j)
    {
        if(memo[i][j] != 0)
        {
            return memo[i][j];
        }
        int path = 1;
        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
            {
                path = max(path, dfs(x, y)+1);
            }
        }
        memo[i][j] = path;
        return path;
    }
};