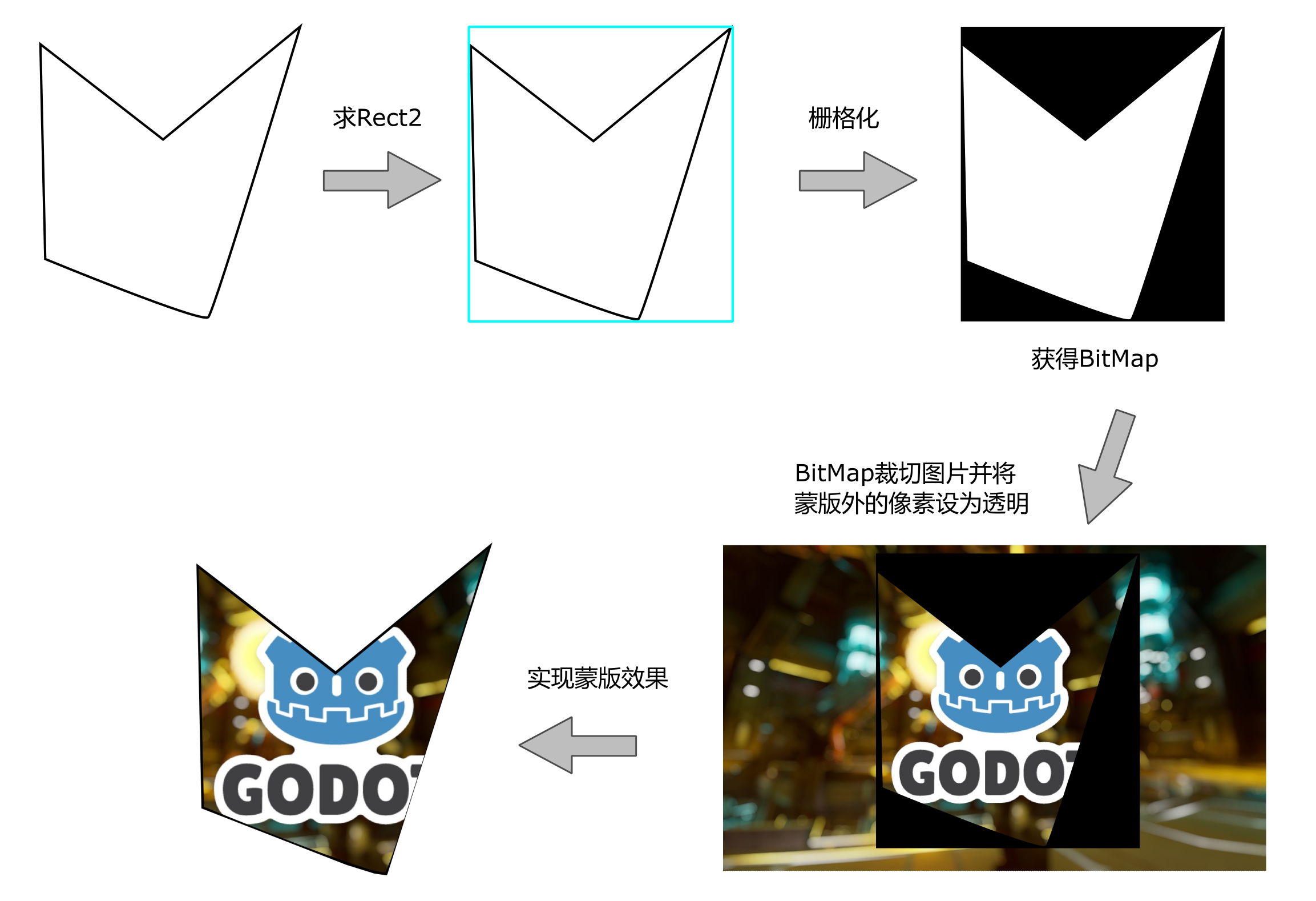
在证明LEAN类型理论的属性前，先对LEAN类型理论所定义的所有推演规则做一个小结，以便后面推导LEAN类型理论的属性。各部分的注解请查看对应文章。

注：这些都是在《LEAN类型理论》中截取出来的，具体内容，读者可参考该论文。

        LEAN类型理论（LEAN Type Theory）有三大部分组成，依赖类型（Dependent Type Theory）、非累积类型宇宙架构（The Hierarchy of Non-cumulative Universes ）、以及 归纳类型（Inductive Type）。

一 依赖类型理论（Dependent Type Theory）及 类型宇宙（Universes）

一、LEAN类型理论里的表示式语法（Syntax of Expression）:

        1. Level 

        2. Expression

        3. Hypotheses

二、赋型规则（Typing Rules）

三、定义上相等规则（Defintional Equality）

四、层次关系

五、算法式定义上相等（Algorithmic Definitional Equality）

六、步进规则（Progress Rules）

小结：以上的规则，完整地定义了，其中的依赖类型理论（Dependent Type Theory）和类型宇宙（Universes）部分。

二 语言扩展（Extensions of Language）

一、let binders

二、Definitions

三 归纳类型（Inductive Type）

一、归纳规范（Inductive Specification K）

二、Large Elimination

三、Elimination Rule of Inductive Type

四、归纳类型的计算规则（Computation Rule，iota reduction）

四 非原生定义（Non-primitive Axioms）

一、商类型（Quotient Type）

二、命题式扩展性（Propositional Extensionality）

        即，两命题能互为条件地推导出来，则两命题相等。

三、选择公理（Axiom of choice）

        即，对于非空类型 α，肯定存在一个函数 choice，能选出该类型中的一个元素。

口