概述
图案(Pattern)填充是一个非常常见的效果。其中又以斜线填充最为简单。本篇就探讨在Godot4.3中如何使用Geometry2D和CanvasItem的绘图函数实现斜线填充效果。
基础思路
Geometry2D类提供了多边形和多边形以及多边形与折线的布尔运算。按照自然的思路,多边形的斜线填充应该属于“多边形与折线的布尔运算”范畴。
第一个问题是如何获得斜线,这条斜线应该满足什么样的条件,除了方向,长度应该怎么确定,又应该从什么地方开始排布,需要阵列多少根?如何才能既满足多边形的填充,又不至于在长度和数量上产生浪费。
围绕这个问题,我思考的答案是——求多边形的矩形包围盒(Rect2):
- 斜线的方向可以用与X轴正方向的夹角定义(与
Vector2中angle()的定义一致) - 初始斜线的一个端点要与
Rect2的某个顶点重合(具体与斜线的方向有关),然后与Rect2的宽边或者高边围成一个直角三角形,斜线的长度就等于直角三角形斜边的长度。 - 通过计算我们可以获得第一条斜线
- 然后按照间隔进行偏移,就可以得到所有斜线
- 偏移的总距离 =
Rect2的宽度或者高度,与第三边的和 - 需要偏移的次数 = 偏移的总距离/斜线间隔
下图是上述思路的图解:
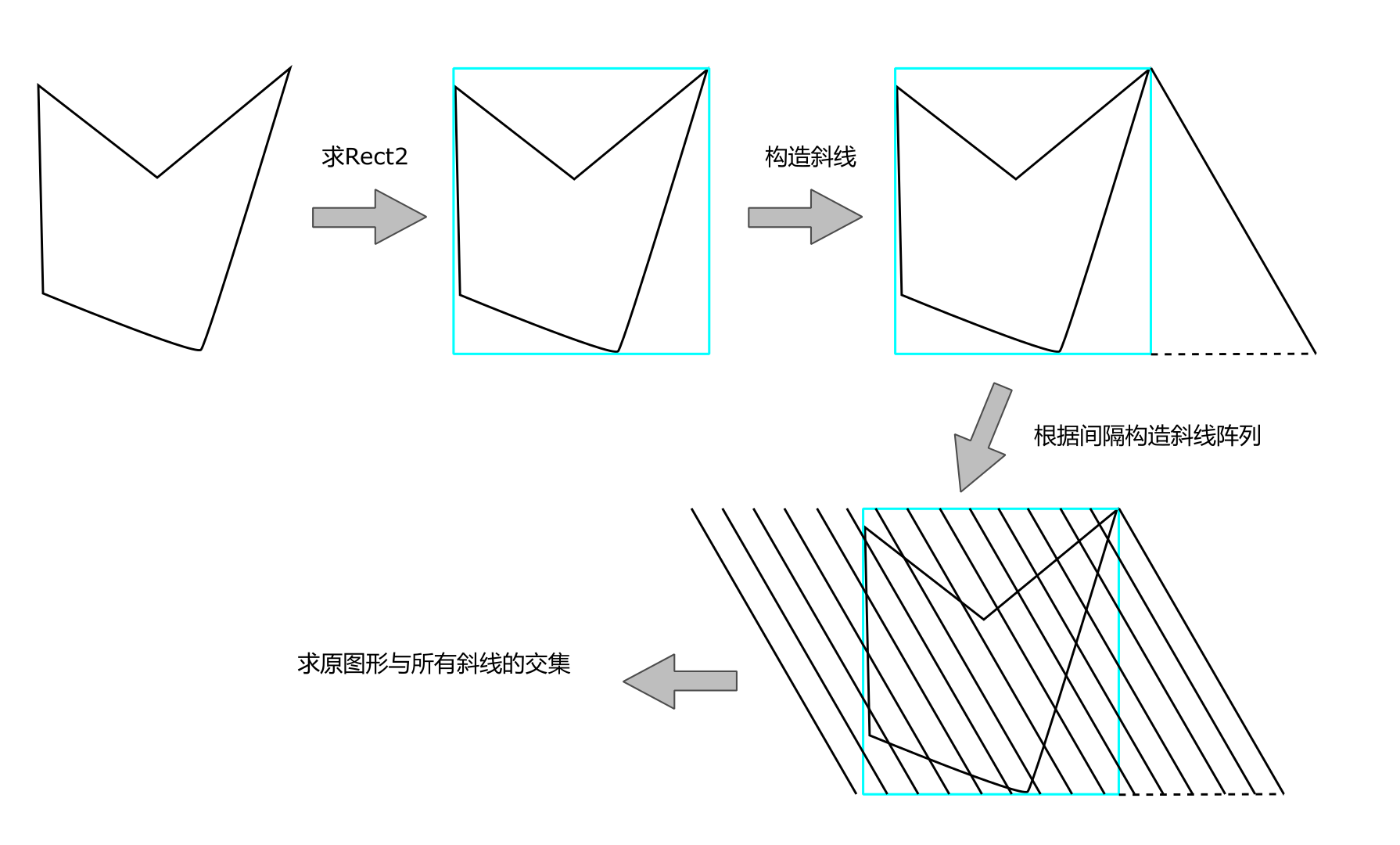
最后就是遍历所有斜线,用Geometry2D求多边形与斜线的交集,最终绘制时只绘制这部分就可以了。
测试
基于上面的思路,我创建了一个基础的测试场景。
根节点代码如下:
# 多边形的斜线填充测试
# 作者:巽星石
# 2024年9月7日22:29:12
@tool
extends Node2D
var shape:PackedVector2Array = [
Vector2(0,0),
Vector2(50,30),
Vector2(100,20),
Vector2(90,80),
Vector2(60,100),
Vector2(0,0),
]
## 形状的轮廓颜色
@export var border_color:=Color.RED:
set(val):
border_color = val
queue_redraw()
## 形状的填充颜色
@export var fill_color:=Color.WHITE:
set(val):
fill_color = val
queue_redraw()
## 斜线的颜色
@export var lines_color:=Color.RED:
set(val):
lines_color = val
queue_redraw()
## 斜线的宽度
@export var lines_width:=1.0:
set(val):
lines_width = val
queue_redraw()
## 斜线与X轴正方向的夹角
@export_range(-360.0,360.0,1.0) var line_angle:=45.0:
set(val):
line_angle = val
queue_redraw()
## 斜线之间的间距
@export var spacing:float = 10.0:
set(val):
spacing = val
queue_redraw()
func _draw() -> void:
# 绘制矩形
var rect = get_rect(shape)
var rect_w = rect.size.x
var rect_h = rect.size.y
draw_rect(rect,Color.AQUA,false,1)
# 根据斜线与X轴夹角计算出其第一条线
var dir = Vector2.RIGHT.rotated(deg_to_rad(line_angle)) # 斜线方向
var length = rect_h / cos(deg_to_rad(90 - line_angle)) # 斜线长度
var p1 = rect.position + Vector2(rect_w,0) # 右上角点
var p2 = p1 + dir * length
# 计算填充长度
var draw_lenth = rect_w + length * sin(deg_to_rad(90 - line_angle))
draw_line(p1,p1 - Vector2(draw_lenth,0),Color.CHARTREUSE,1)
# 计算需要阵列的斜线数目
var old_lines:PackedVector2Array = [] # 存储所有原始斜线的数组
var lines:PackedVector2Array = [] # 存储所有斜线的数组
var steps = draw_lenth / spacing
for i in range(steps+1):
var line:PackedVector2Array = [p1,p2]
line = Transform2D(0,Vector2(-spacing * i,0)) * line
old_lines.append(line[0])
old_lines.append(line[1])
var jiao = Geometry2D.intersect_polyline_with_polygon(line,shape) # 求交集部分
if jiao.size() > 0:
lines.append(jiao[0][0])
lines.append(jiao[0][1])
# 绘制多边形填充
draw_polygon(shape,[fill_color])
# 绘制斜线填充
draw_multiline(old_lines,Color.AQUA,lines_width)
# 绘制斜线填充
draw_multiline(lines,lines_color,lines_width)
# 绘制多边形轮廓
draw_polyline(shape,border_color,1)
# 获取图形的矩形
func get_rect(shape:PackedVector2Array) -> Rect2:
# 拆分出X坐标和Y坐标数组
var x_arr = []
var y_arr = []
for p in shape:
x_arr.append(p.x)
y_arr.append(p.y)
# 最小值构成Rect2的offset
var pos = Vector2(x_arr.min(),y_arr.min())
# 最大值 - pos = Rect2 的 size
var siz = Vector2(x_arr.max(),y_arr.max()) - pos
return Rect2(pos,siz)
测试效果:
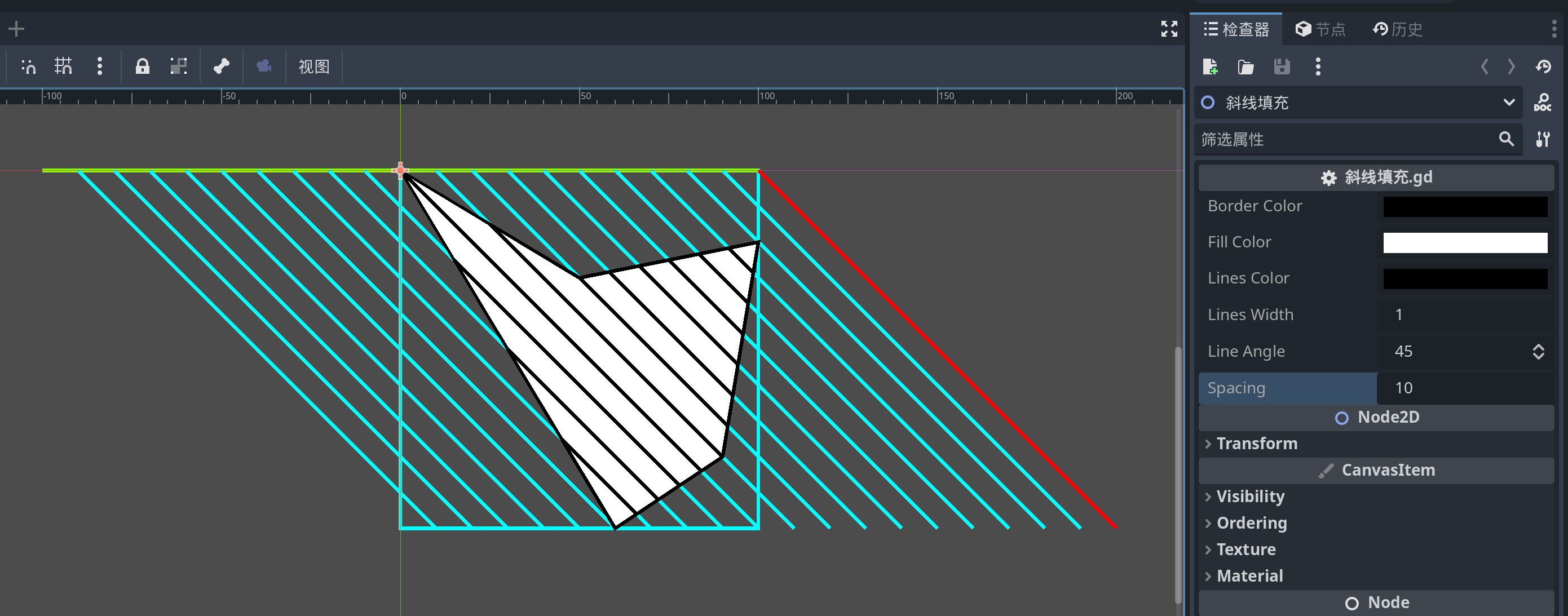
其中:
- 绿色线为斜线需要偏移的总距离
- 红色为第一条斜线
- 海蓝色线为通过偏移获得的斜线。
- 原始多边形填充默认为白色,轮廓和斜线都为黑色。
下图是基于line_angle属性值从45°逐渐递增的动态演示:

线太宽时的错误
线宽在一两像素时,而且多边形绘制了轮廓线的效果下,上面的斜线填充看起来十分完美。但是当线宽大于一定数值时,用Polyline形式就出现明显的毛病了,因为所有斜线都被绘制为类似矩形的形状。实际上如果去除多边形的轮廓线,即使是1像素宽的线,也是矩形,求得的斜线也是不完美的。
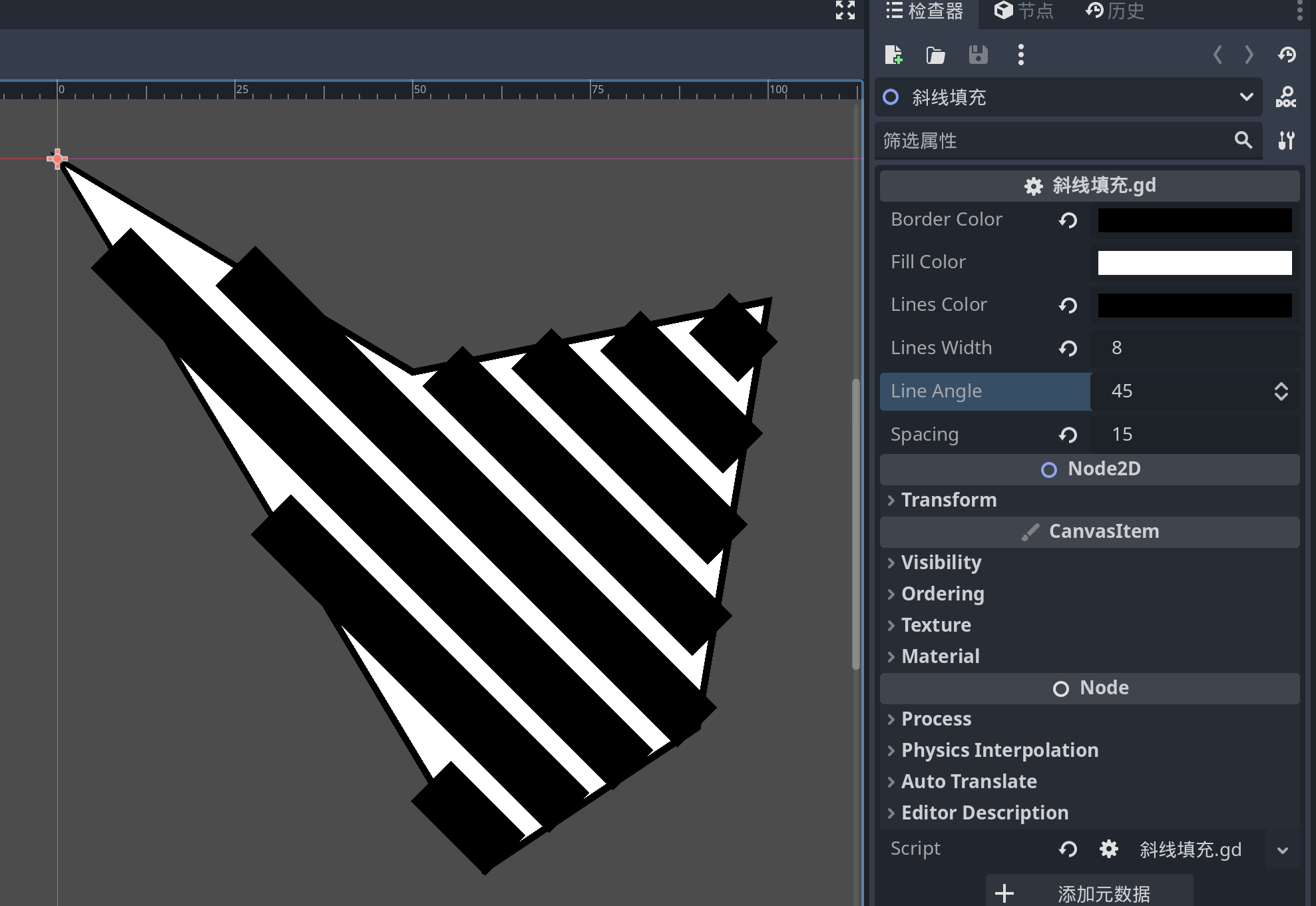

所以解决方案就是,将斜线看做是多边形。
而这就需要将折线转变为多边形,好在Geometry2D提供了一个叫offset_polyline()的方法,可以将Polyline通过像素偏移的方式,转化为相应宽度的多边形。
所以问题又变成了求解多边形与多边形交集的问题。
改进后的代码如下:
# 多边形的斜线填充测试(偏移矩形法)
# 作者:巽星石
# 2024年9月8日00:51:37
# 2024年9月8日01:14:22
@tool
extends Node2D
var shape:PackedVector2Array = [
Vector2(0,0),
Vector2(50,30),
Vector2(100,20),
Vector2(90,80),
Vector2(60,100),
Vector2(0,0),
]
## 形状的轮廓颜色
@export var border_color:=Color.BLACK:
set(val):
border_color = val
queue_redraw()
## 形状的填充颜色
@export var fill_color:=Color.WHITE:
set(val):
fill_color = val
queue_redraw()
## 斜线的颜色
@export var lines_color:=Color.BLACK:
set(val):
lines_color = val
queue_redraw()
## 斜线的宽度
@export var lines_width:=1.0:
set(val):
lines_width = val
queue_redraw()
## 斜线与X轴正方向的夹角
@export_range(-360.0,360.0,1.0) var line_angle:=45.0:
set(val):
line_angle = val
queue_redraw()
## 斜线之间的间距
@export var spacing:float = 10.0:
set(val):
spacing = val
queue_redraw()
func _draw() -> void:
# 绘制矩形
var rect = get_rect(shape)
var rect_w = rect.size.x
var rect_h = rect.size.y
#draw_rect(rect,Color.AQUA,false,1)
# 根据斜线与X轴夹角计算出其第一条线
var dir = Vector2.RIGHT.rotated(deg_to_rad(line_angle)) # 斜线方向
var length = rect_h / cos(deg_to_rad(90 - line_angle)) # 斜线长度
var p1 = rect.position + Vector2(rect_w,0) # 右上角点
var p2 = p1 + dir * length
# 计算填充长度
var draw_lenth = rect_w + length * sin(deg_to_rad(90 - line_angle))
#draw_line(p1,p1 - Vector2(draw_lenth,0),Color.CHARTREUSE,1)
# 计算需要阵列的斜线数目
var old_lines:PackedVector2Array = [] # 存储所有原始斜线的数组
var lines:PackedVector2Array = [] # 存储所有交集斜线的数组
var old_line_rects:Array[PackedVector2Array] = [] # 存储原始斜线的的偏移矩形
var line_polygons:Array[PackedVector2Array] = [] # 存储交集斜线的的偏移矩形
var steps = draw_lenth / spacing
for i in range(steps+1):
var line:PackedVector2Array = [p1,p2]
line = Transform2D(0,Vector2(-spacing * i,0)) * line
old_lines.append(line[0])
old_lines.append(line[1])
# 根据斜线求偏移矩形
var line_rect = Geometry2D.offset_polyline(line,lines_width/2.0)
old_line_rects.append_array(line_rect)
#draw_colored_polygon(line_rect[0],lines_color)
# 求折线形式的交集
var jiao = Geometry2D.intersect_polyline_with_polygon(line,shape) # 求交集部分
if jiao.size() > 0:
lines.append(jiao[0][0])
lines.append(jiao[0][1])
# 求偏移矩形的交集
var jiao_polygon = Geometry2D.intersect_polygons(line_rect[0],shape) # 求交集部分
if jiao_polygon.size() > 0:
line_polygons.append(jiao_polygon[0])
# 绘制多边形填充
draw_polygon(shape,[fill_color])
# 绘制斜线多边形
for polygon in line_polygons:
draw_colored_polygon(polygon,lines_color)
# 绘制原始斜线
#draw_multiline(old_lines,Color.AQUA,lines_width)
# 绘制第一条原始斜线
#draw_line(p1,p2,Color.RED,1)
# 绘制斜线填充
#draw_multiline(lines,lines_color,lines_width)
# 绘制多边形轮廓
draw_polyline(shape,border_color,1)
# 获取图形的矩形
func get_rect(shape:PackedVector2Array) -> Rect2:
# 拆分出X坐标和Y坐标数组
var x_arr = []
var y_arr = []
for p in shape:
x_arr.append(p.x)
y_arr.append(p.y)
# 最小值构成Rect2的offset
var pos = Vector2(x_arr.min(),y_arr.min())
# 最大值 - pos = Rect2 的 size
var siz = Vector2(x_arr.max(),y_arr.max()) - pos
return Rect2(pos,siz)
部分测试截图如下:
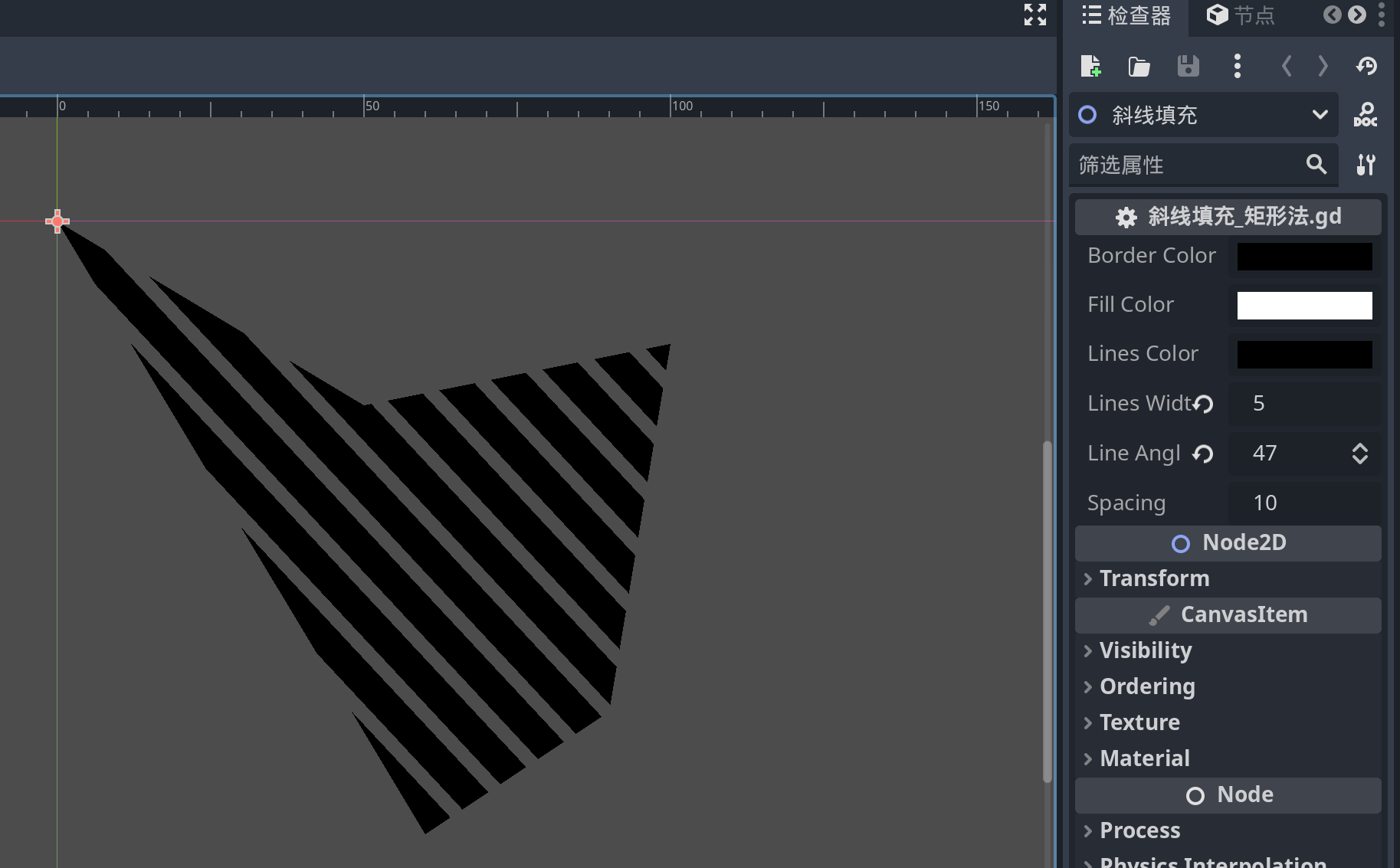
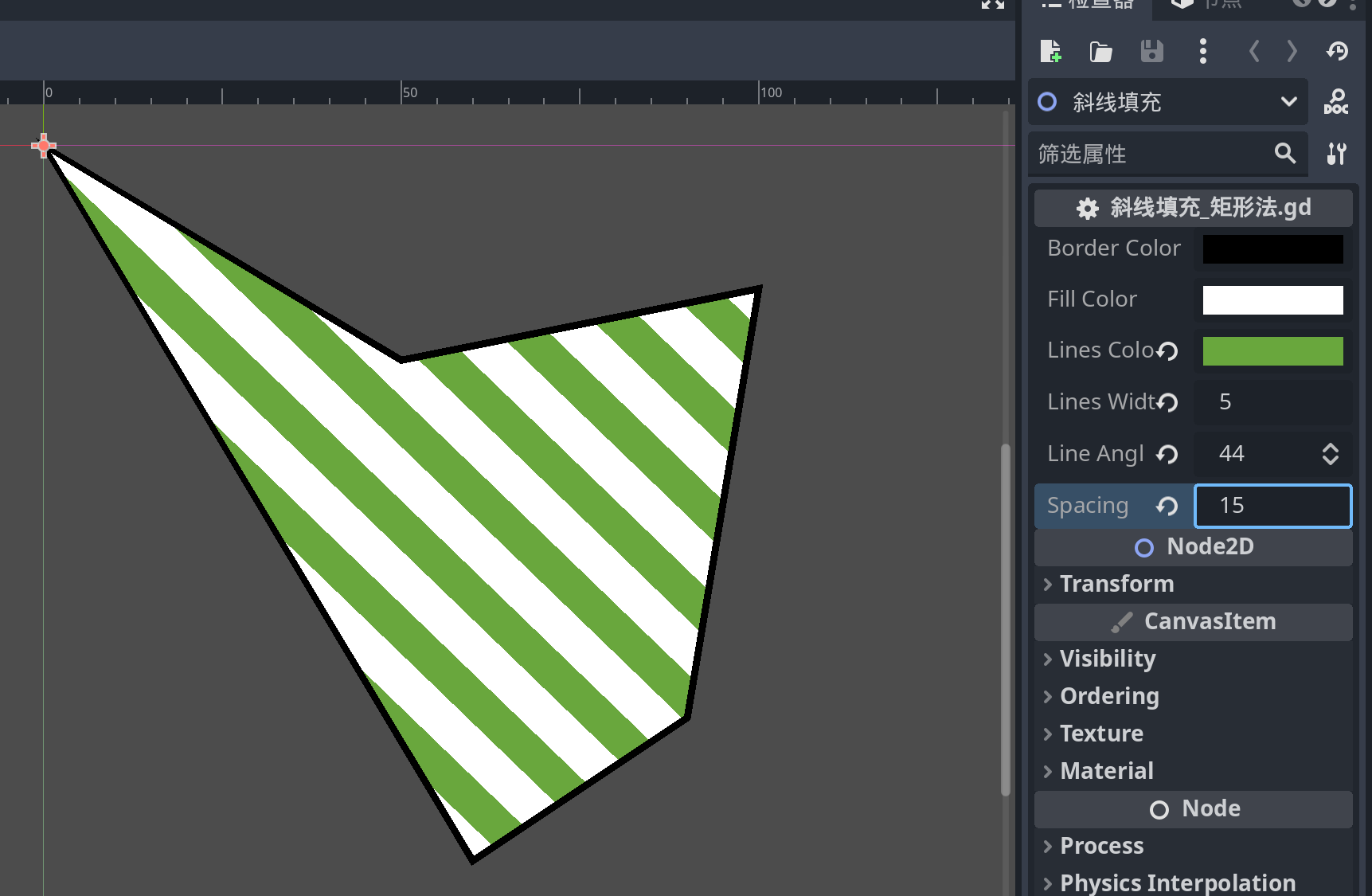
总结
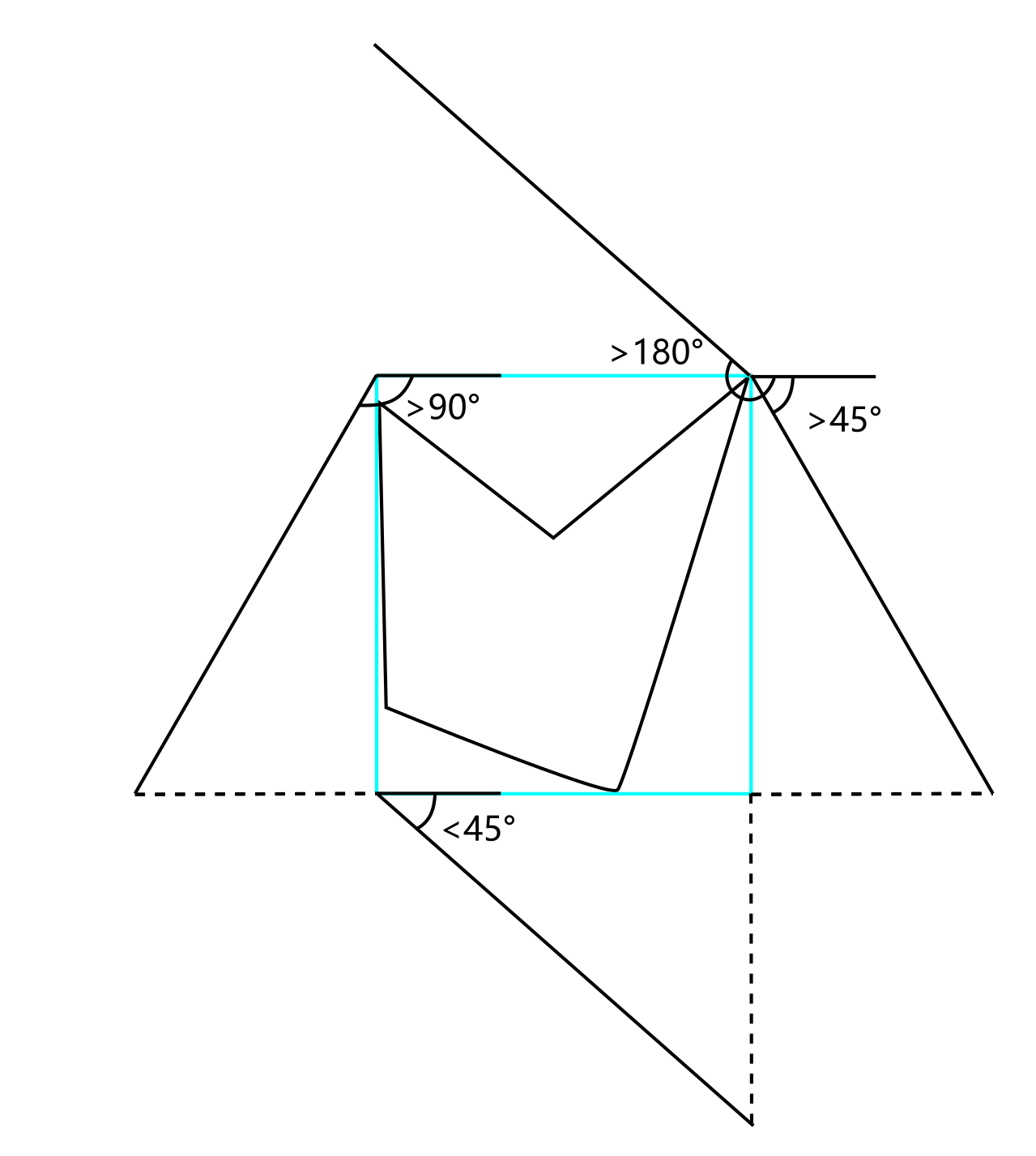
本篇简要描述了多边形斜线填充算法的简单思路,当然这里只是初步的测试,只适用于凸多边形在0到90度之间的情况。
上面例子中的凹多边形在一定0到90度之间的某些清下也会出现错误,如下图:
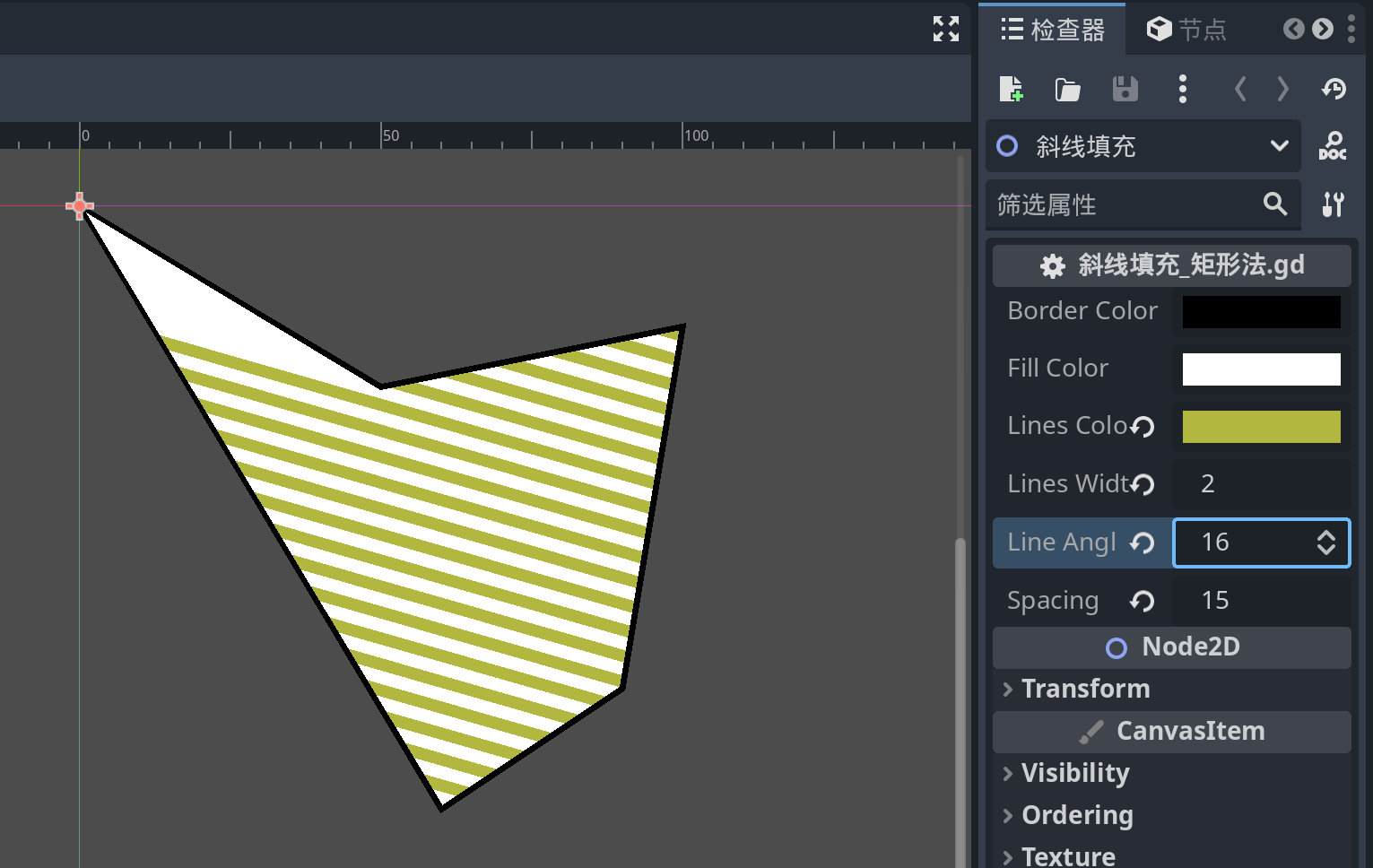
这种错误其实也可以通过将凹多边形拆解为若干凸多边形求解。
0到90度之外的求解本篇并没有补足,但是大致思路是一致的。
展望
斜线填充只是最简单的一种图案(Pattern)填充形式。但在拿下斜线填充之后,剩下的无论是波浪线、棋盘格等等都有了基础的求解思路。
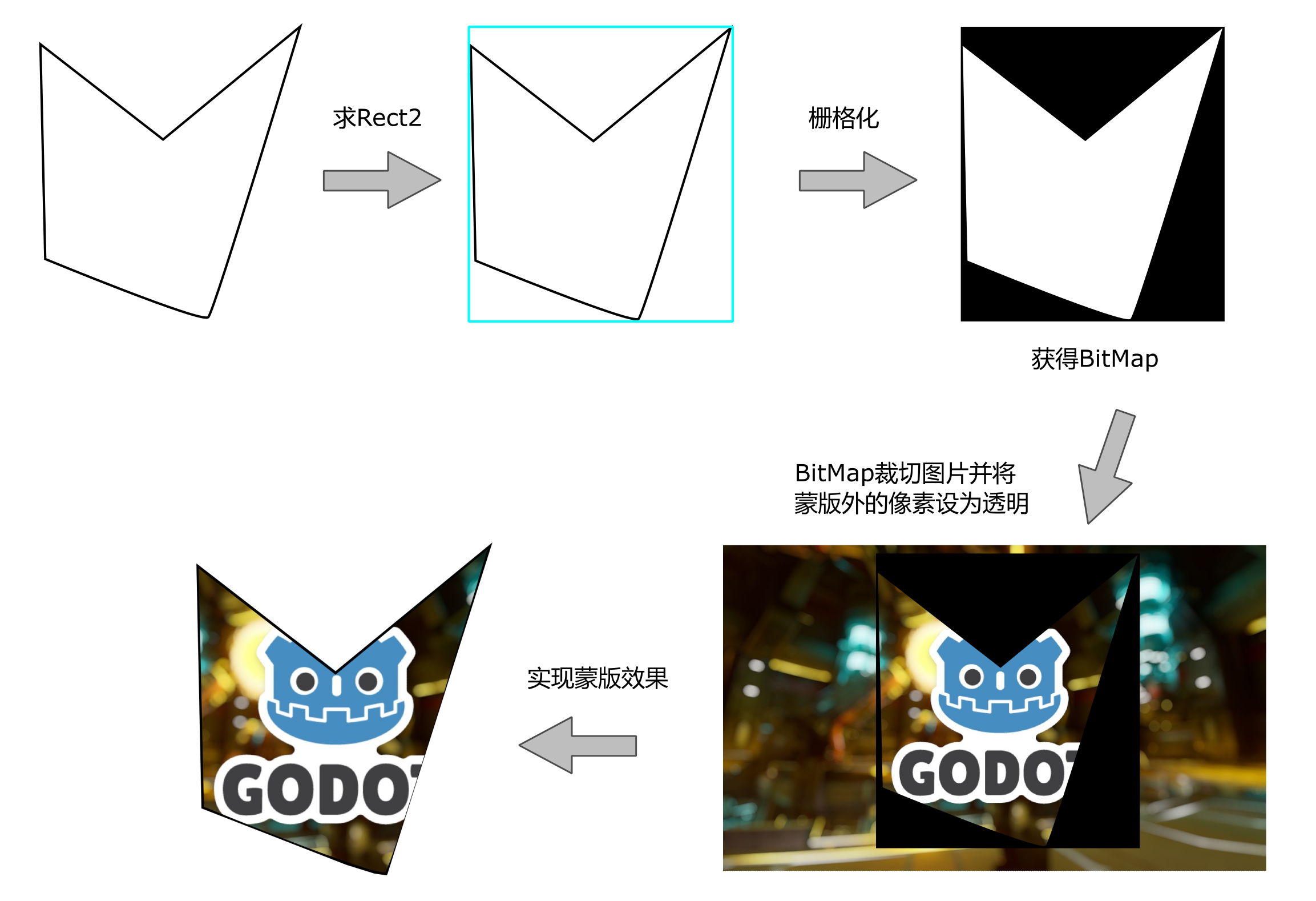
矢量蒙版和图片填充
蒙版是一个像素图概念,基于Godot的BitMap类型,可以创建和还原硬边缘的蒙版效果。
而通过矢量多边形栅格化,我们可以创建BitMap,从而实现矢量蒙版,而有了矢量蒙版,就可以实现多边形的图案填充。


![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)
















