文章目录

前言：
AVL 的插入
- 寻找插入位置
- 更新平衡因子
- 调整AVL
- - 右旋
  - 左旋
  - 左右双旋
  - 右左双旋
完整代码

前言：

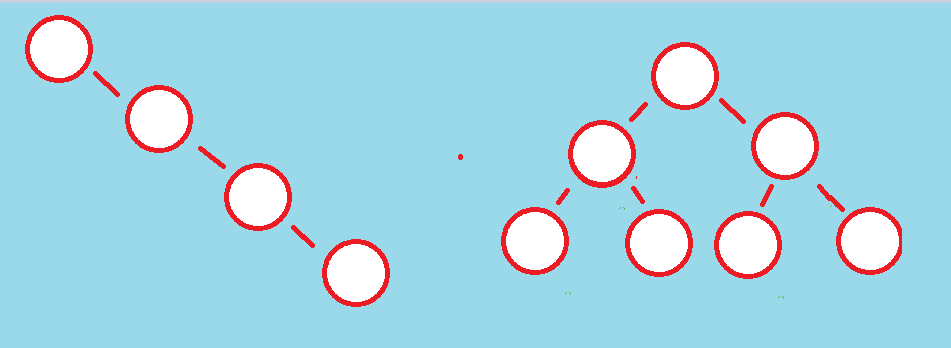
我们知道二叉排序树的搜索效率很高，能达到(logn)的时间复杂度，但是当元素有序导致二叉搜索树变成了一个长条（图左）的时候，就会导致搜索速率大大降低，所以我们需要对二叉搜索树做出改进：让二叉搜索树能够在插入元素的时候及时调整自己的结构（右图），这就是 AVL 树（高度平衡的二叉搜索树）

在这里插入图片描述

AVL 的插入

所以今天我们的重点就是 AVL 树的插入，并且每一次插入结点，都要调整树的高度，保持树的高度平衡

而不同于普通的二叉搜索树，AVL 树的结点还优点不同，我们不仅需要左右孩子节点，还需要一个指向父亲节点的引用，除此之外，还有 bf 字段——balanced factor，也就是平衡因子，定义为右子树高度 - 左子树高度，于是对于 AVL 树的节点就有了以下定义：

static class TreeNode {
    public TreeNode parent ; // 父亲结点
    public TreeNode left;    
    public TreeNode right;
    // 平衡因子, 右子树增加则 bf ++, 左子树增加则 bf --
    public int bf; // 平衡因子
    public int val;
    public TreeNode(int val) {
        this.val = val;
    }
}

寻找插入位置

对于一个要插入的节点，第一步肯定就是寻找插入位置
如果根节点为空，那么这个新节点就是根节点，否则，寻找插入位置
这个比较简单，不是本文重点，直接上这部分的代码

    public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if (root == null) {
            root = node;
            return true;
        }

        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return true; // 重复节点
            }
        }
        // 至此 cur 为空，parent 为 cur 的父节点
        // 完成节点的插入
        if (parent.val > val) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        node.parent = parent; // 双向连接

	}

等到循环终止的时候，parent 的左孩子或者右孩子就是待插入节点，这时在分别判断一下，更新一下 parent 的孩子引用和新节点的 parent 引用即可

更新平衡因子

这个新插入的节点我们称为「newNode」, 每次插入一个新节点必然需要调整「从该节点到根节点的平衡因子」
所以我们让 cur = newNode, parent = cur.parent,从 newNode 开始往根节点开始更新平衡因子

如果 cur 为 parent 的左孩子, 那么 parent 的 bf 就需要 -1 (左子树高度增加), 相反, 如果 cur 为 parent 的右孩子, 那么 parent 的 bf 就需要 +1 (右子树高度增加), 于是我们就有了这个代码, 先别急, 慢慢来

// parent = cur.parent;
 cur = node;
 // 开始向上搜索, 重新计算平衡因子, 平衡这棵树
 while (parent != null) {  // 因为是「向上更新 bf」, 所以 parent 自然到根节点的parent就结束了
     if (cur == parent.left) {
         parent.bf --;
     } else {
         parent.bf ++;
     }

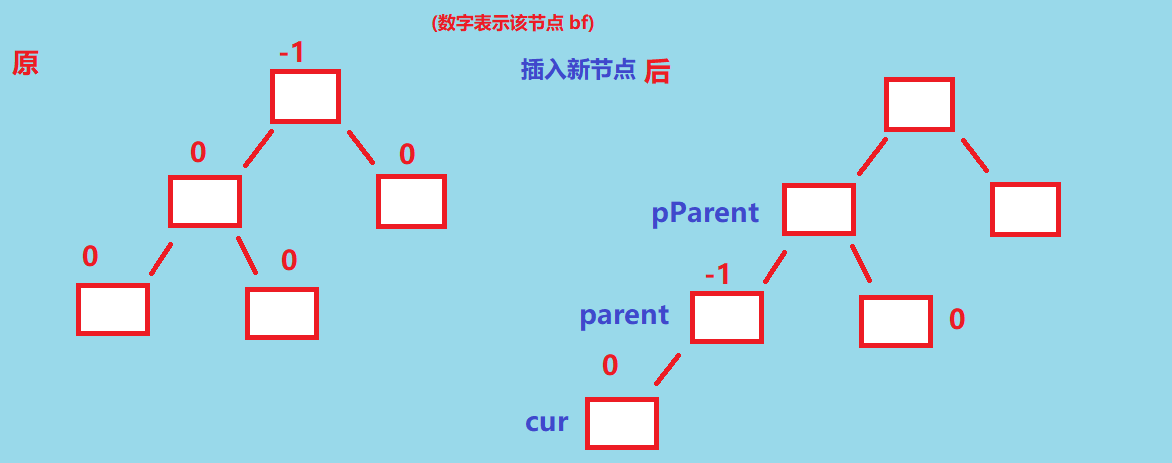
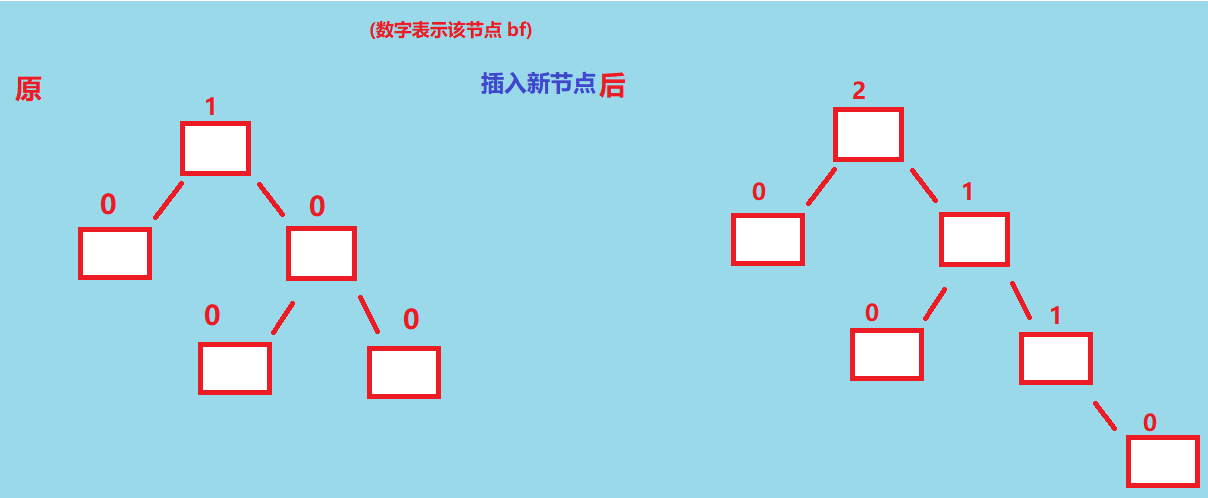
在向上更新的过程中, 如果更新完之后, parent 的平衡因子为 1 或者 - 1, 那么我们还是要继续向上更新的, 如下图, 插入 cur 结点后, 「parent 的 bf 变为了 -1, 而 pParent.bf 明显不是原来的 0 」了, pParent.bf 是需要重新更新的

所以当更新完 parent 结点的 bf 的时候, parent.bf 还是 1 或 -1的时候, 我们还需要向上更新

在这里插入图片描述
因此:

// 更新完parent.bf后, bf 还是 if 中的情况
if (parent.bf == 1 || parent.bf == -1) {
   // 继续向上调整
    cur = parent;
    parent = cur.parent;
}

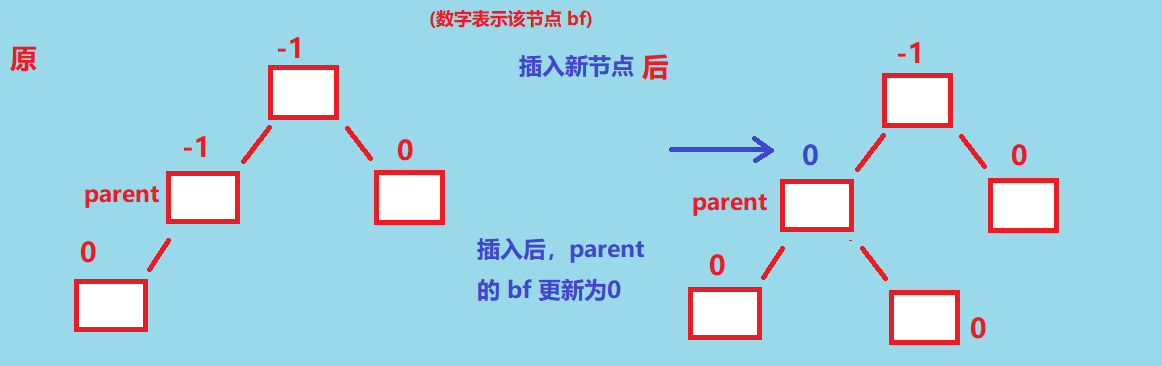
而如果新增 newNode 之后, parent.bf 更新完后 parent.bf = 0是什么情况 ? 如下图, 如果某个 parent 更新完后 parent.bf = 0, 那么就不需要再向上更新了

在这里插入图片描述
于是就有:

// 更新完 parent.bf 后, 还出现 if 中的情况
if (parent.bf == 0) {
     break;
}

那么当更新完后, parent.bf == 2 || parent.bf == -2 的时候, 那就是这个树此时不是高度平衡的状态了, 这时候就需要进行旋转了 !!! 正文开始 !

调整AVL

右旋

首先第一种情况, 如果parent.bf == -2 && cur.bf == -1, 从这两个 bf 变量的情况上来看, 就是这个树左边比较长。插入结点前后如下👇

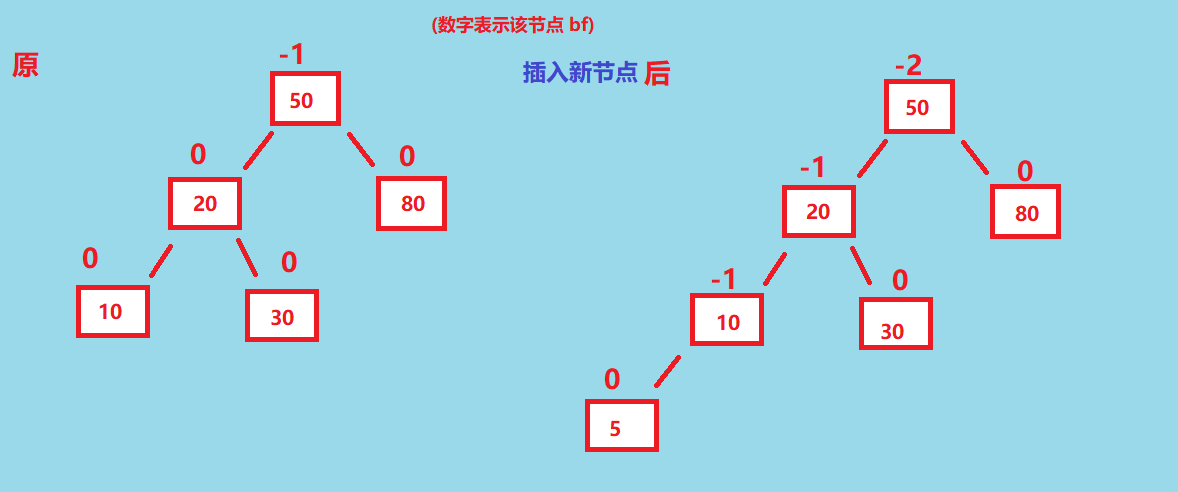
在这里插入图片描述

那么这时候, 我们就需要对这个树进行右旋, 如图, 把 lson 提起来, 然后把它的右孩子交给 parent 的左孩子, 于是这个左旋就完成了

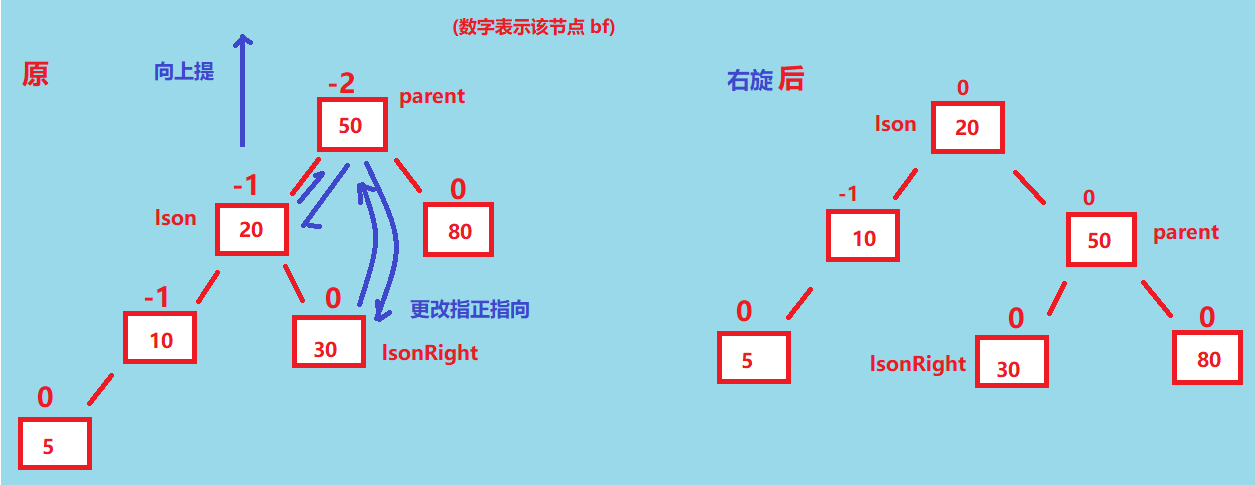
在这里插入图片描述
对于当前子树左旋后, 我们还需要更新原 parent.parent的孩子指向, 说的有点复杂, 给个图就懂了

如果 parent == root, 那么旋转后, 根节点就是 lson, 让root = lson 即可 , 这个情况跟上面这个图一样👆
如果 pParent.left == parent || pParent.right == parent 那么就重新连接一下「旋转后的子树」, 这个应该不难理解，如下图, 旋转后, pParent 的孩子结点应该更新为 lson, 同理 lson 的父亲结点也要更新

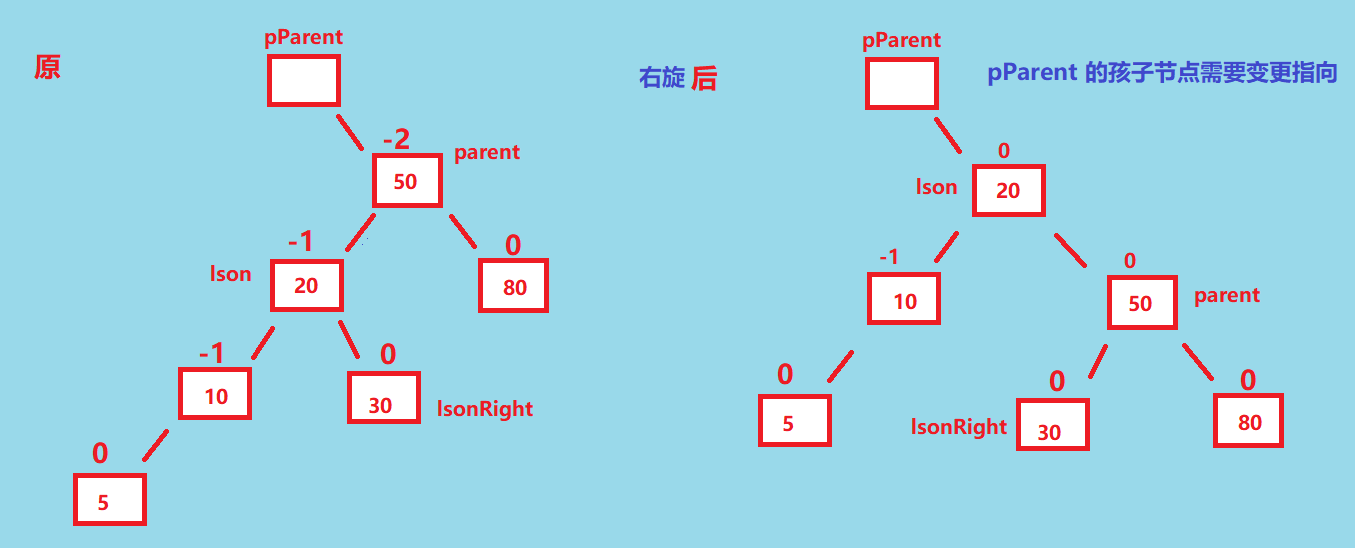
在这里插入图片描述
随后, 再更新相应结点的平衡因子, 这种情况下 lson.bf 和 parent.bf 都会变成 0

而另一种情况, 也就是 lsonRight = null 的情况，如下 👇，这种情况 lson 和 parent 的 bf 也都会变成 0。

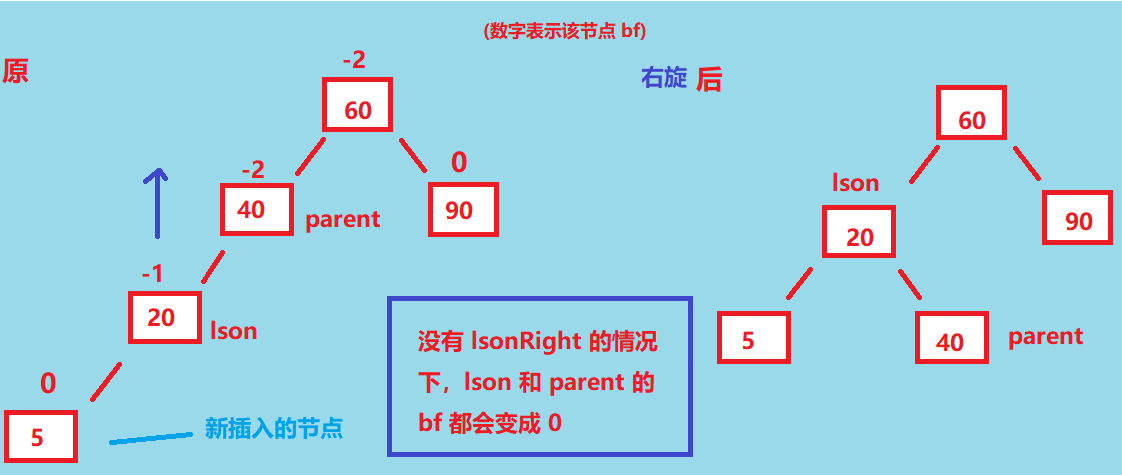
在这里插入图片描述

所以右旋之后, parent 和 lson 的平衡因子都会变成 0

最后, 再给出上述操作的代码

    // 右旋, 把 parent 的 左孩子提起来
    private void rotateRight(TreeNode parent) {
        // parent 的左孩子
        TreeNode lson = parent.left;
        // lson 的右孩子
        TreeNode lsonRight = lson.right;
        // parent 的父节点
        TreeNode pParent = parent.parent;


        lson.right = parent;
        parent.parent = lson;
        // 这里特殊处理一下, 有可能 lsonRight 为空
        if (lsonRight != null) { 
            lsonRight.parent = parent;
        }
        parent.left = lsonRight;

        // 再讨论根节点, 如果 parent 本来是根节点
        if (root == parent) {
            root = lson;
            lson.parent = null;
        } else {
            if (pParent.left == parent) {
                pParent.left = lson;
            } else {
                pParent.right = lson;
            }
            lson.parent = pParent;
        }
        lson.bf = parent.bf = 0;
    }

左旋

第二种情况，当parent.bf == 2 && cur.bf == 1 的时候，从这两个变量上看，就是右子树比较长，插入元素前后如下👇

在这里插入图片描述

这时候右树比较长，所以需要进行左旋，操作图如下👇，rson 的左孩子(即rsonLeft)交给 parent 的右孩子

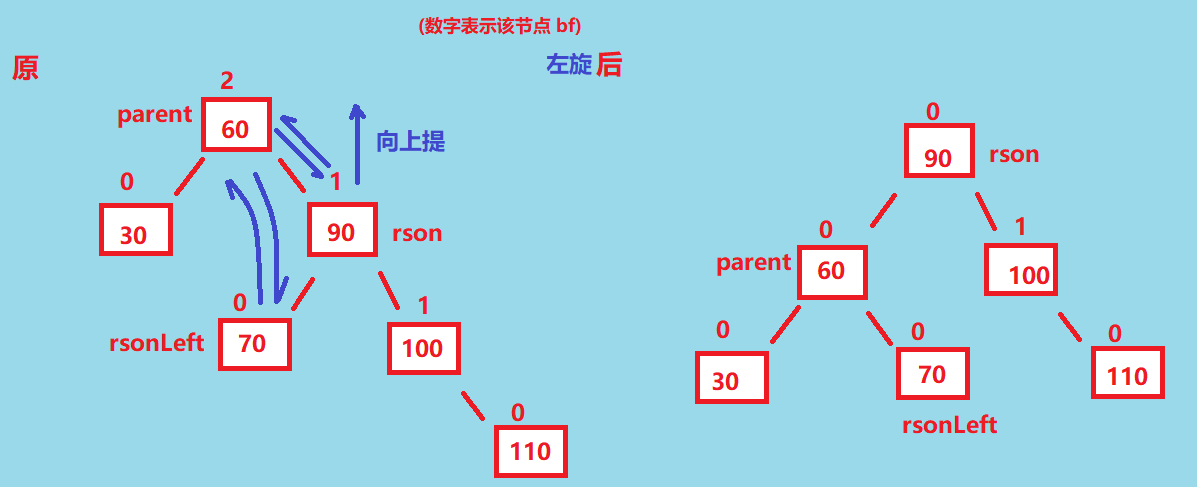
在这里插入图片描述
左旋和右旋很相似，也需要重新判断旋转后的子树的父亲节点pParent，同时无论 rsonLeft 存不存在，最终 rson.bf 和 parent.bf 都会变成 0，这里就不赘述了

所以啊, 单旋之后 parent 和 lson(或者rson) 的平衡因子都置为 0 即可

    // 右子树太高, 左旋
    private void rotateLeft(TreeNode parent) {
        TreeNode rson = parent.right;
        TreeNode rsonLeft = rson.left;
        TreeNode pParent = parent.parent;

        rson.left = parent;
        parent.parent = rson;
        if (rsonLeft != null) { // 再 rsonLeft 存在的情况下才更新 rsonLeft 的父亲节点
            rsonLeft.parent = parent;
        }
        parent.right = rsonLeft;

        if (parent == root) {
            root = rson;
            rson.parent = null;
        } else {
            if (pParent.left == parent) {
                pParent.left = rson;
            } else {
                pParent.right = rson;
            }
            rson.parent = pParent; // 双向连接
        }
        // 再更新平衡因子
        rson.bf = parent.bf = 0;
    }

左右双旋

接下来还有两种情况，我们再来讨论其中的第一种：
如果parent.bf = -2, cur.bf = 1，从这两个变量和图形来说，有种中间比较长的感觉
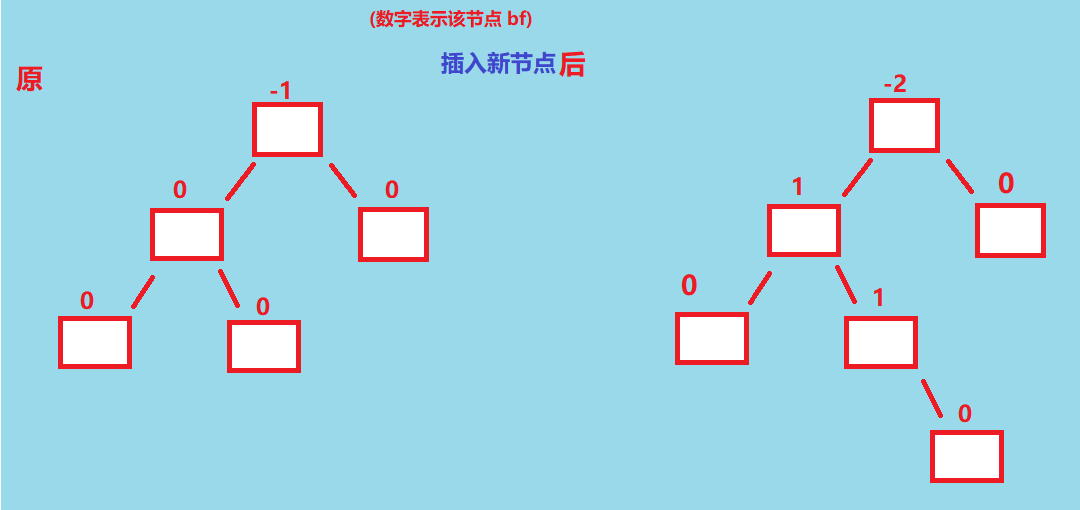
在这里插入图片描述
这种情况下，不论是一次左旋还是一次右旋都无法达成平衡，左旋后高度差还是能能达到 2，左旋后如下图👇。
只进行一次右旋也是一样，笔者就偷懒不画了

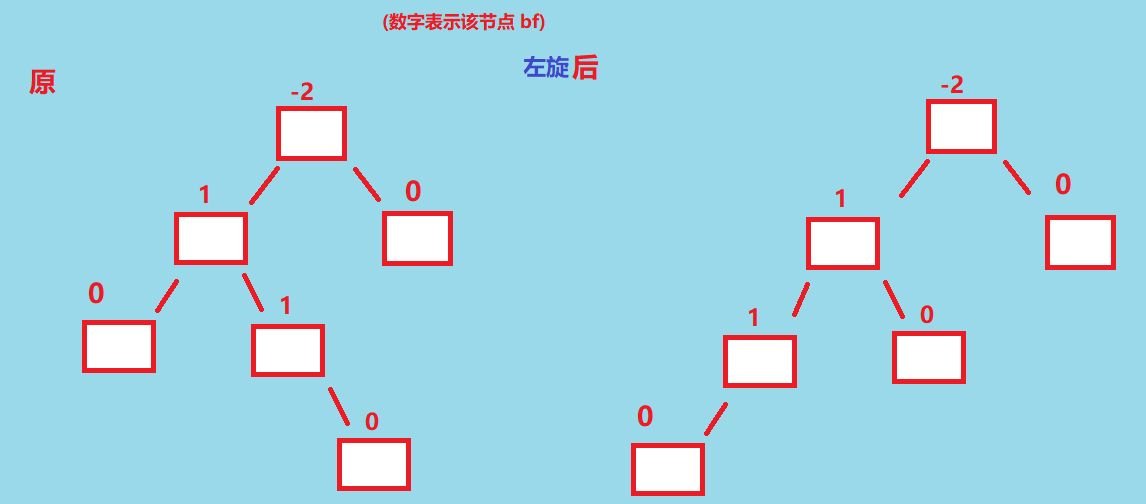在这里插入图片描述这种情况下就只能够通过两次旋转来重新调整为平衡——先左旋再右旋, 最终让 lsonRight 变成旋转后的根节点，我们再画个图看看这个过程

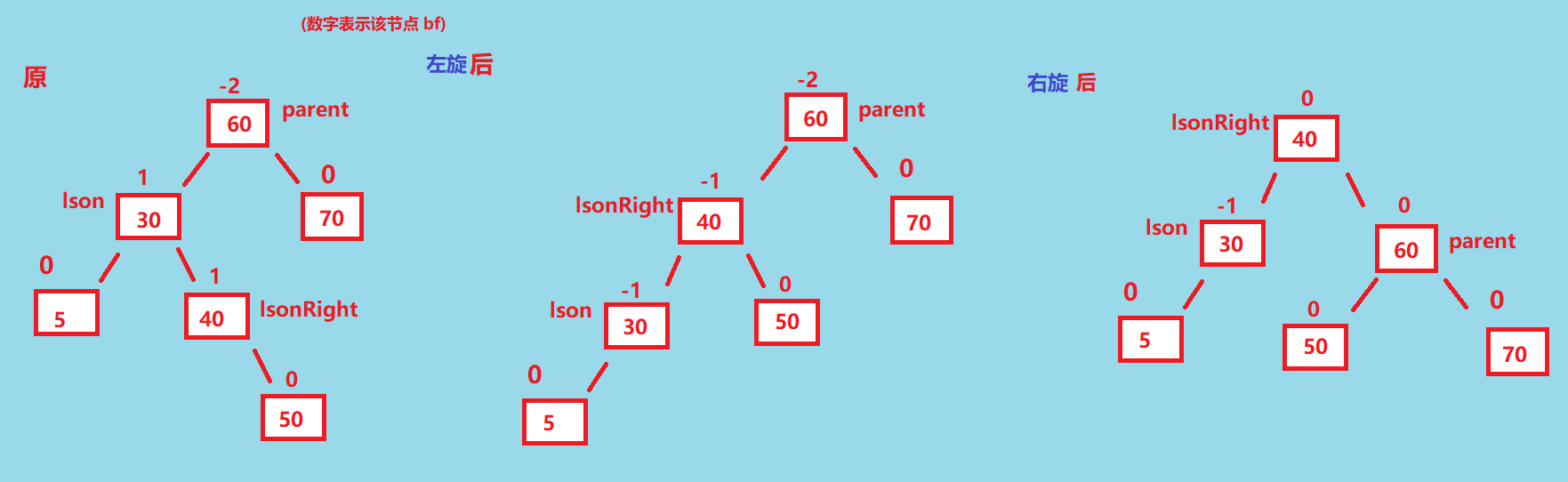在这里插入图片描述以上就是左右双旋的旋转过程, 然后我们再讨论一下平衡因子的变化情况
双旋的平衡因子调整分为三种情况： lsonRight.bf = 1 || lsonRight.bf == -1 || lsonRight.bf == 0

上面我这种画法 lsonRight.bf = 1, 最终 parent, lson, lsonRight 的因子最终变化：lson.bf = -1, lsonRight.bf = 0, parent.bf = 0
而如果 lsonRight.bf == 0 的时候，这种情况下这三个节点的 bf 值是不会发生变化的，不需要做处理
如果lsonRight.bf = -1，这种情况最终变化：lson.bf = 0, lsonRight.bf = 0, parent.bf = 1，我们画个图看看：

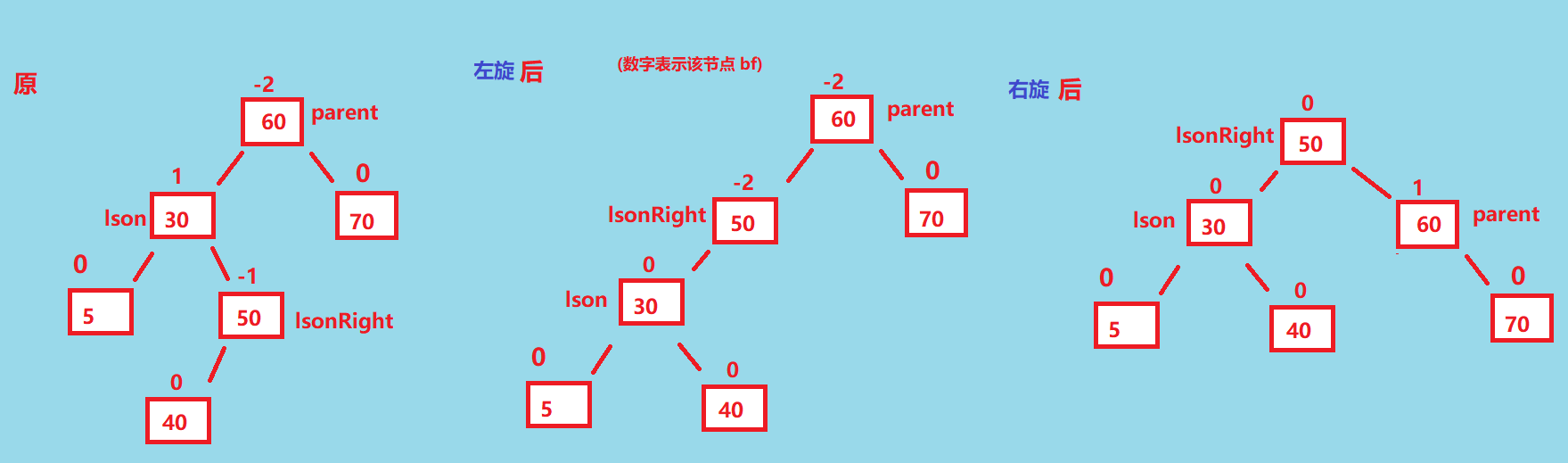在这里插入图片描述到这里左右双旋就完成了，稍微有点复杂，但是理解了左旋和右旋应该是能够接受的，加油，这里上代码

    private void rotateLR(TreeNode parent) {
        TreeNode lson = parent.left;
        TreeNode lsonRight  = lson.right;
        int bf = lsonRight.bf;

        rotateLeft(lson);
        rotateRight(parent);

        // 再分情况调整 平衡因子
        if (bf == 1) {
            lson.bf = -1;
            lsonRight.bf = 0;
            parent.bf = 0;
        } else if (bf == -1) { // bf == -1
            lson.bf = 0;
            lsonRight.bf = 0 ;
            parent.bf = 1;
        } // 至此 bf == 0，不做任何处理
    }

右左双旋

最后一个就是右左双旋了, 这个和左右…是类似的, 我们画一次熟悉熟悉, 如果是parent.bf = 2, cur.bf = -1, 插入结点后如下图, 有种中间比较长的感觉

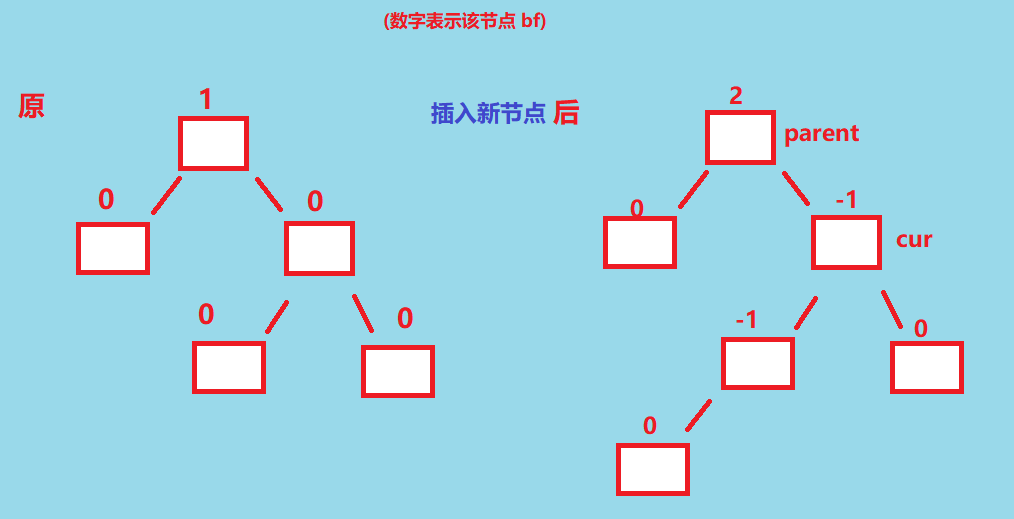
在这里插入图片描述
这情况和左右双旋的情况一样, 单次右旋或者左旋都是无法调整为平衡的
我们需要先右旋再左旋, 示意图如下, 还是一样定义三个关键结点 parent, rson, rsonLeft, 并且最终旋转后的子树根节点为 rsonLeft

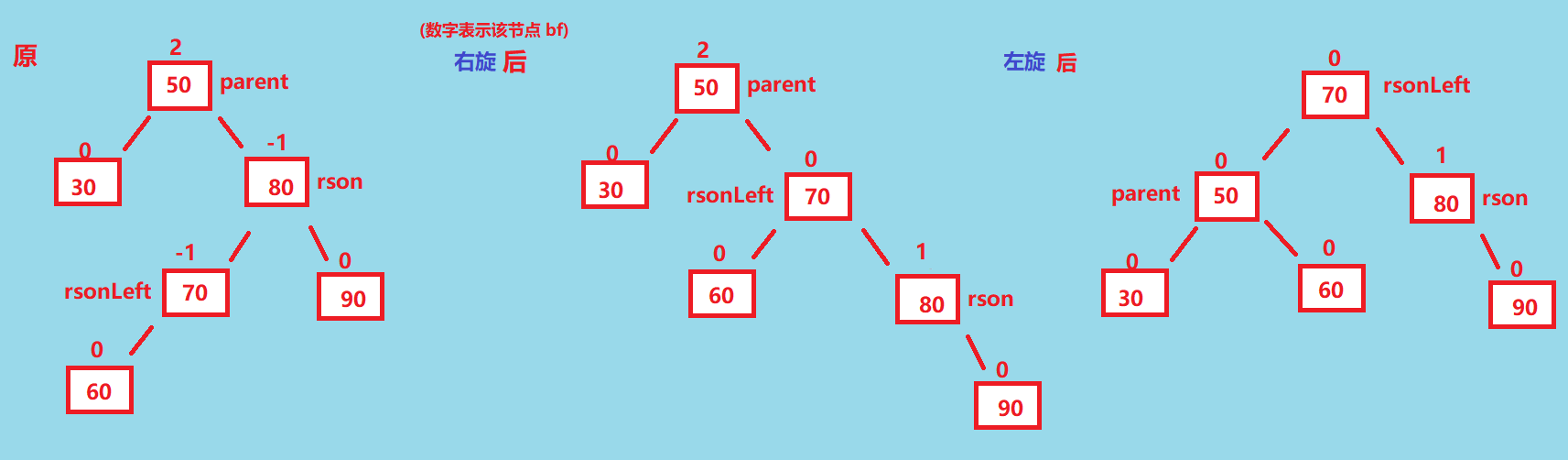在这里插入图片描述然后是平衡因子的调整, 还是一样分为三种情况: rsonLeft.bf == -1 || rsonLeft == 0 || rsonLeft == 1

如果rsonLeft.bf == -1, 那么这种情况就和上面这张图一样, 最终因子变成parent.bf = 0, rsonLeft.bf = 0, rson = 1
如果rsonLeft.bf == 0, 这种情况不用做任何操作
如果rsonLeft.bf == 1, 最终因子变成parent.bf = -1, rsonLeft.bf = 0, rson.bf = 0, 我们再画个图看看

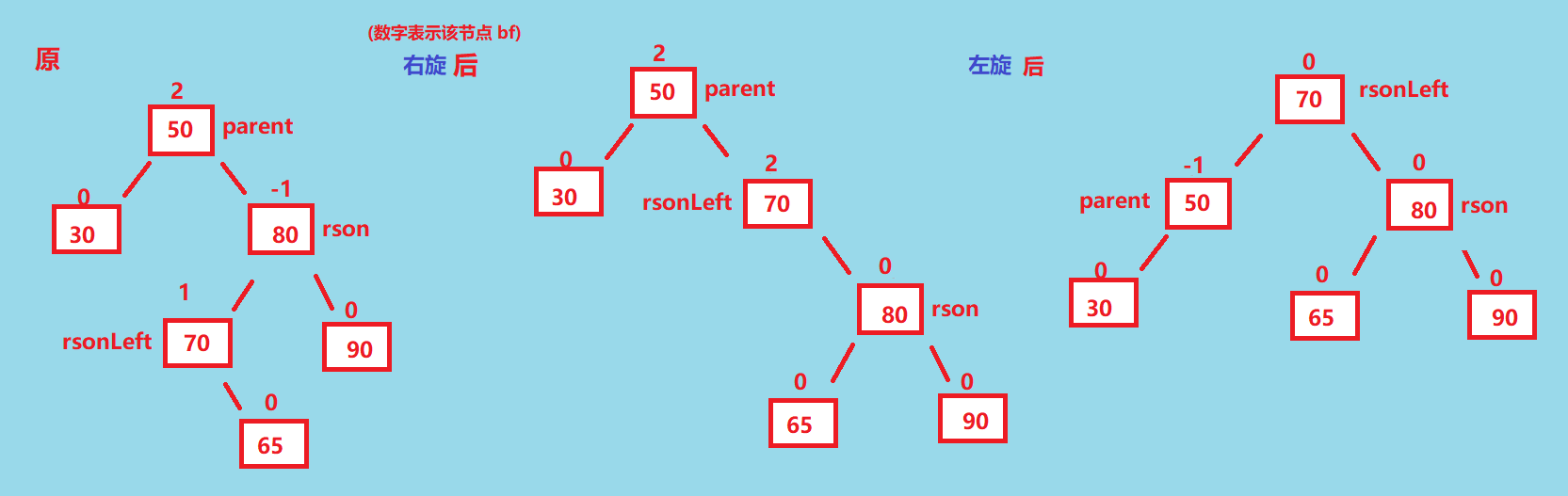在这里插入图片描述到这里就完成了, 上代码

    private void rotateRL(TreeNode parent) {
        TreeNode rson = parent.right;
        TreeNode rsonLeft = rson.left;
        int bf = rsonLeft.bf;

        rotateRight(rson); // 复用之前的左旋右旋即可
        rotateLeft(parent);


        if (bf == 1) {
            parent.bf = -1;
            rsonLeft.bf = 0;
            rson.bf = 0;
        } else if (bf == -1) { // bf = -1
            parent.bf = 0;
            rsonLeft.bf = 0;
            rson.bf = 1;
        }
    }

完整代码

/**
 * 模拟实现：高度平衡的二叉搜索树
 */
public class AVL {
    static class TreeNode {
        public TreeNode parent ;
        public TreeNode left;
        public TreeNode right;
        // 平衡因子, 右子树增加则 bf ++, 左子树增加则 bf --
        public int bf;
        public int val;
        public TreeNode(int val) {
            this.val = val;
        }
    }

    public TreeNode root;

    public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if (root == null) {
            root = node;
            return true;
        }

        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return true; // 重复节点
            }
        }
        // 至此 cur 为空，parent 为 cur 的父节点
        // 完成节点的插入
        if (parent.val > val) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        node.parent = parent; // 双向连接

        // parent = cur.parent;
        cur = node;
        // 开始向上搜索, 重新计算平衡因子, 平衡这棵树
        while (parent != null) {
            if (cur == parent.left) {
                parent.bf --;
            } else {
                parent.bf ++;
            }

            // 如果说 parent 的结点重新变为 0, 则说明该树平衡, 不需要再调整
            if (parent.bf == 0) {
                break;
            } else if (parent.bf == 1 || parent.bf == -1) {
                // 还算正常, 继续向上结算
                cur = parent;
                parent = cur.parent;
            } else {
                // 否则 parent 的 bf 为 2, 或者 parent 的 bf 为 -2
                if (parent.bf == -2) {
                    if (cur.bf == -1) {
                        // 左子树太高了, 需要右旋
                        rotateRight(parent);
                    } else {
                        // parent.bf == -2 && cur.bf == 1
                        // 这时候就需要 左旋 再 右旋
                        rotateLR(parent);
                    }
                } else {
                    // parent.bf == 2
                    if (cur.bf == 1) {
                        rotateLeft(parent);
                    } else { // cur.bf == -1
                        // 这时候需要先 左旋 和 右旋
                        rotateRL(parent);
                    }
                }
                // 完成了一次旋转就能够达成平衡
                break;
            }
        }
        return true;
    }

    private void rotateRL(TreeNode parent) {
        TreeNode rson = parent.right;
        TreeNode rsonLeft = rson.left;
        int bf = rsonLeft.bf;

        rotateRight(rson);
        rotateLeft(parent);


        if (bf == 1) {
            parent.bf = -1;
            rsonLeft.bf = 0;
            rson.bf = 0;
        } else if (bf == -1) { // bf = -1
            parent.bf = 0;
            rsonLeft.bf = 0;
            rson.bf = 1;
        }
    }

    private void rotateLR(TreeNode parent) {
        TreeNode lson = parent.left;
        TreeNode lsonRight  = lson.right;
        int bf = lsonRight.bf;

        rotateLeft(lson);
        rotateRight(parent);

        // 再分情况调整 平衡因子
        if (bf == 1) {
            lson.bf = -1;
            lsonRight.bf = 0;
            parent.bf = 0;
        } else if (bf == -1) { // bf == -1
            lson.bf = 0;
            lsonRight.bf = 0 ;
            parent.bf = 1;
        }
    }

    // 右子树太高, 左旋
    private void rotateLeft(TreeNode parent) {
        TreeNode rson = parent.right;
        TreeNode rsonLeft = rson.left;
        TreeNode pParent = parent.parent;

        rson.left = parent;
        parent.parent = rson;
        if (rsonLeft != null) {
            rsonLeft.parent = parent;
        }
        parent.right = rsonLeft;

        if (parent == root) {
            root = rson;
            rson.parent = null;
        } else {
            if (pParent.left == parent) {
                pParent.left = rson;
            } else {
                pParent.right = rson;
            }
            rson.parent = pParent; // 双向连接
        }
        // 再更新平衡因子
        rson.bf = parent.bf = 0;
    }

    // 右旋, 把 parent 的 左孩子提起来
    private void rotateRight(TreeNode parent) {
        // parent 的左孩子
        TreeNode lson = parent.left;
        // lson 的右孩子
        TreeNode lsonRight = lson.right;
        // parent 的父节点
        TreeNode pParent = parent.parent;


        lson.right = parent;
        parent.parent = lson;
        if (lsonRight != null) {
            lsonRight.parent = parent;
        }
        parent.left = lsonRight;

        // 再讨论根节点, 如果 parent 本来是根节点
        if (root == parent) {
            root = lson;
            lson.parent = null;
        } else {
            if (pParent.left == parent) {
                pParent.left = lson;
            } else {
                pParent.right = lson;
            }
            lson.parent = pParent;
        }
        lson.bf = parent.bf = 0;
    }