使用的动机

定义：将对象根据它们的位置存储在数据结构中，来高效地定位对象。

在游戏中，AI向最近的敌人攻击是很常见的，但如果有很多单位的话，他们AI需要频繁的查找单位，然后在检测是不是距离最近的单位，时间复杂度是o(n ^ 2)

之所以会出现这个问题，是因为我们没有指明潜在的对象顺序。假如我们游戏的所有单位都只在一条直线上，我们只需要二分查找就可以找到最近对象了。操作系统中，有着局部性原理，我们也可以根据游戏物体的位置来存储对象，这样就能更快的找到他们

注意事项：

空间分区的存在是为了将O(n)或者O(n²) 的操作降到更加可控的数量级。 你拥有的对象越多，这就越重要。相反的，如果n足够小，也许不需要担心这个

这不仅能够用于存储可移动的游戏对象，还可用于静态美术等场景资源。如果对象发生移动，我们需要在数据结构中重新追踪该对象，这也会增加CPU消耗。

实现方法

实现模式有很多种，都有各自的性能优势

固定网格

将整个游戏战场分割为固定大小的网格中，每个格子分别存储一组单位，对象在网格中的存储方式应该是双向链表，因为他增删结点比较迅速

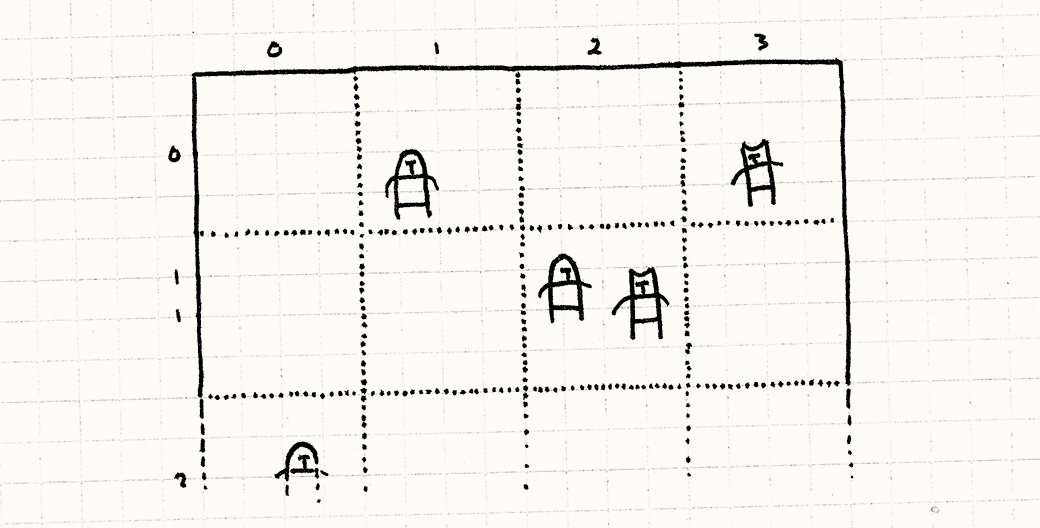
在单位移动需要改变位置时，我们需要先判断是否穿越了格子的边界，如果穿越，我们需要先移除再添加到网格中

对于近距离攻击来说，只运算网格中的单位相互攻击是没啥大问题的。但是对于其他的攻击方式形成了新的问题，比如有一个远距离攻击的法师单位或者是能够冲锋的骑兵单位，就不能只判断单一网格。

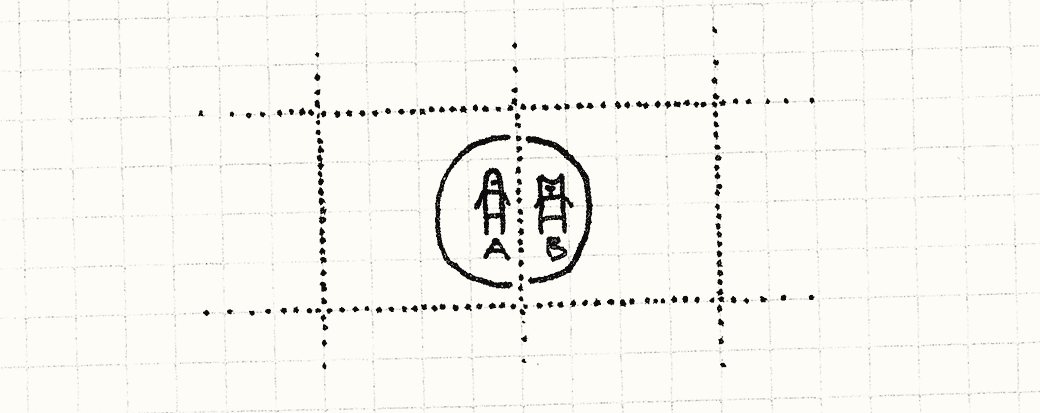
这时候我们不仅需要比较同一网格，还需要比较邻近网格对象

空间划分依据

层次和平面划分

层次划分：

层次空间划分将空间分成几个区域。 然后，如果其中一个区域还包含多个对象，再划分它。 这个过程递归进行，直到每个区域都有少于最大数量的对象在其中。

• 处理空区域时更有效率，大片的空区域在单个划分上，不需要遍历很多个空的小空间
• 处理密集空间时也更有效率，当对象都聚集在一起时，每个网格仍然只有少量单位。

平面划分：

内存使用量确定，因为划分不会有增删，分区的内存使用量固定

在对象改变位置时更新得更快，层次更新则需要多层级调整，甚至改变层次划分

是否与对象有关

与对象有关：

固定划分中，移动单位意味着只需要从网格中删除，在加入到另一个网格中就可以了，但不是固定划分的话就需要改变边界，对象可以增量添加。 添加对象意味着找到正确的划分然后放入，这点可以一次性完成，没有任何性能问题。

与对象无关：

在BSP和KD树中这样各地适应对象划分世界，可以让每个部分都包含接近数目的对象，划分边界时需要考虑每一边各有多少对象。

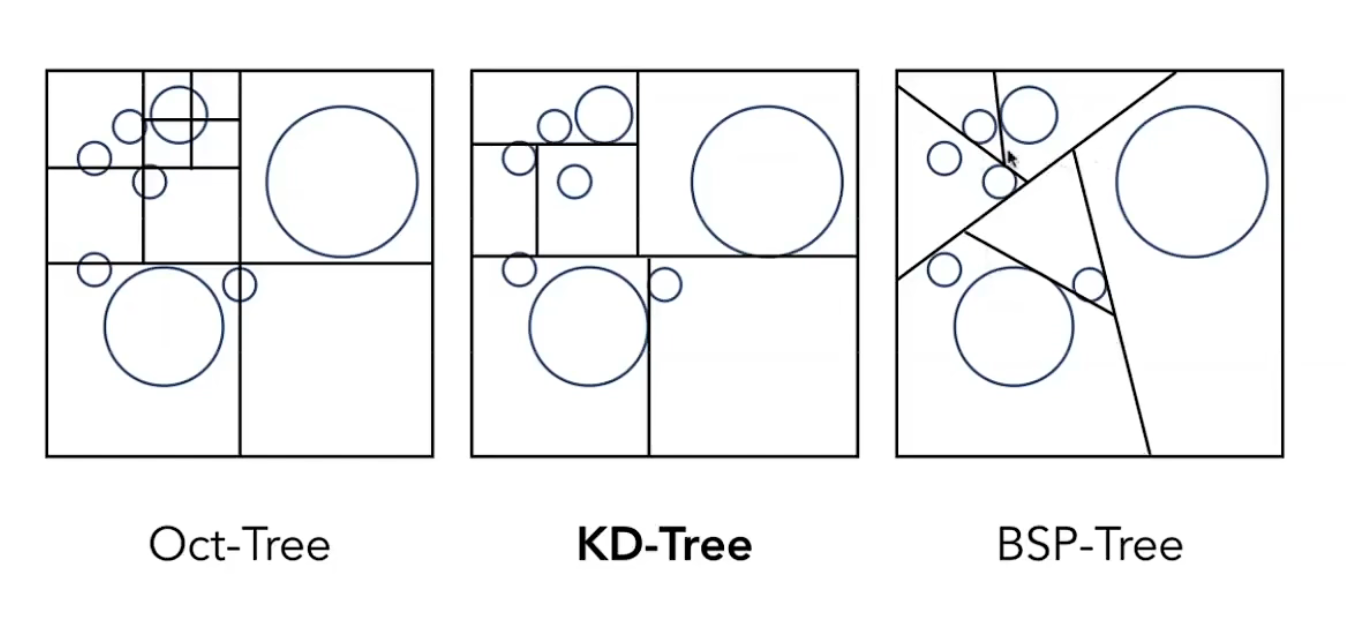
Oct-Tree：八叉树，对于三维空间中的一个场景将其横竖切三刀，切成八块，在二维空间表现为四叉。。

KD-Tree：k-d树每次只会选取一个基轴方向进行分割，比如二维空间中先沿x方向分割，然后再沿y轴方向分割。

BSP-Tree：也是每次划分选择一个方向将空间分成两部分，与KD-Tree相比它不是横平竖直的划分，不好计算

其中八叉树可以拥有两者的优点：对象能够批量增加马，移动对象很快，分区是平衡的

存储是否唯一

空间划分还有一个值得注意的问题，空间分区是否是游戏对象存储的唯一地方

**如果唯一:**这能够减少内存消耗

**如果不是：**如果我们需要用除了位置关系外其他的方式来访问对象，比如特定种类的兵种，有了其他的数据保存结构我们能够更快的访问

总结

每种空间分区数据结构基本上都是将一维数据结构扩展成更高维度的数据结构。

• 网格是连续的桶排序
• BSPs，k-d trees和包围盒是线性搜索树
• 四叉树和八叉树是多叉树