快速排序(QuickSort)-归并排序(MergeSort)[java编写]

news2025/1/6 18:03:15

1. 快速排序

1.1 基本概述

快速排序采用分治思想，即在一个无序的序列中选取一个任意的基准元素pivot，利用pivot 将待排序的序列分成两部分，前面部分元素均小于或等于基准元素，后面部分均大于或等于基准元素，然后采用递归的方法分别对前后两部分重复上述操作，直到将无序序列排列成有序序列。、

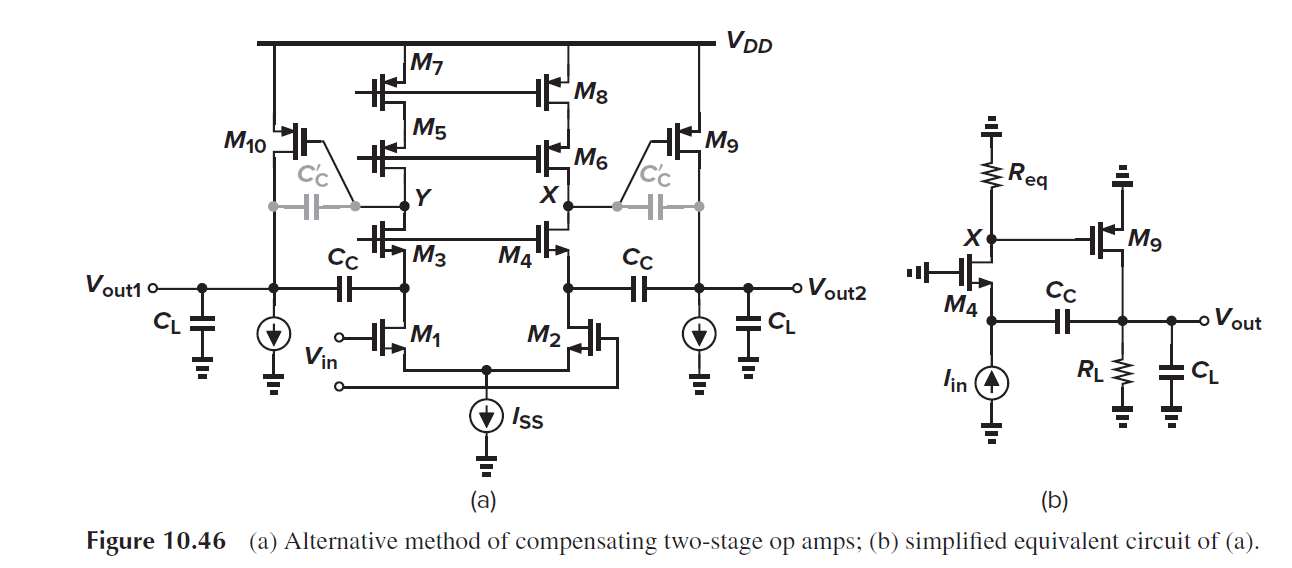
1.2 图解

1.3 快速排序的代码实现(java)

class QuickSort {
    public static void sort(int[] array) {
        sortSection(array, 0, array.length - 1);
    }
    
    private static void sortSection(int[] array, int start, int end) {
        // 递归的baseCase
        if(start >= end) {
            return;
        }
        // 递归分块并排序
        int p = partition(array,start,end);
        sortSection(array, start, p - 1);
        sortSection(array, p + 1, end);
    }
    
    /**
     * partition 方法目的在于将目标数组分以pivot为界，分为两部分，并返回pivot应在的的位置-                            
       biggest_smallest
     * @param array    目标数组
     * @param start    开始位置
     * @param end      结束位置
     * @return         返回分割后的pivot位置-biggest_smallest
     */
    
    private static int partition(int[] array,int start,int end) {
        int pivot = array[start];
        int biggest_smallest = start;
        int tmp;
        // 以pivot为隔板，小的放左边，大的放右边
        for(int i = start + 1; i <= end; i++) {
            if(array[i] < pivot) {
                biggest_smallest++;
                tmp = array[biggest_smallest];
                array[biggest_smallest] = pivot;
                array[i] = tmp;
            }
        }
        array[start] = array[biggest_smallest];
        array[biggest_smallest] = pivot;
        return biggest_smallest;
    }
}

1.4 快速排序的时间复杂度

快速排序是一种常用的排序算法，它的时间复杂度在不同情况下有所不同。在最佳情况下，快速排序的时间复杂度为O(n log n)，而在最差的情况下，其时间复杂度为O(n ^ 2)。平均情况下，快速排序也能达到O(nlogn) 的时间复杂度。

快速排序的性能高度依赖于选择的基准值，如果每次能将数组分为两个大小大致相等的子数组，那么快速排序的效率最高。在这种情况下，排序过程可以看作是一个平衡二叉树，其中每个节点的操作时间为O(n)，树的高度为O(logn)。因此，整个排序过程的时间复杂度为O(n logn)。

在最差情况下，如果每次选择的基准值都是最小或最大的元素，那么数组将不会被平均分割，导致递归深度为O(n)，每次的操作时间仍未O(n)，因此总的时间复杂度为O(n^2)。

尽管快速排序在最差情况下的时间复杂度较高，但由于其在平均情况下的高效性，以及它的就地排序特性(不需要额外的存储空间)，快速排序通常优于其他排序算法，如归并排序。此外，快速排序的局部性引用优势使得它在实际应用中的表现通常比理论分析更好。

1.5 快速排序的空间复杂度

快速排序的空间复杂度主要由递归调用栈产生。在最佳情况下，递归树的深度为O(log n)，因此空间复杂度也为O(log n)，在最差的情况下，递归树退化为线性链，空间复杂度为O(n)。平均情况下，空间复杂度同样为O(log n)。

2. 归并排序

2.1 基本概述

归并排序是一种高效的排序算法，由约翰.冯.诺依曼于1945年发明，它利用了分治法(Divide and Conquer) 的策略来实现排序。归并排序的核心思想是将一个大问题分解成小问题解决，然后将小问题的解决结果合并以解决原来的大问题。

归并排序将待排序的数组分成两部分，对每部分递归地应用归并排序，然后将两个有序的子数组合并成一个有序的数组。这个过程一直重复，直到数组完全有序。归并排序的过程可以用一棵完全二叉树来形象地表示，其中每个节点表示一个排序操作或合并操作。

2.2 图解

先拆分

后合并

2.3 归并排序的代码实现

class MergeSort {
    public static void sort(int [] array){
        sortSection(array,0,array.length - 1);
    }
    private static void sortSection(int[] array,int start,int end){
        // 递归的baseCase
        if(start == end) {
            return;
        }
        // 通过递归实现了数据按归并排序算法的拆分
        int mid = (start + end) / 2;
        sortSection(array,start,mid);
        sortSection(array,mid + 1,end);
        // 调用merge方法对数据进行合并
        merge(array,start,mid + 1,end);
    }

    /*
    merge 方法实现了两块数据的合并阶段
    */
    private static void merge(int[] array,int start,int start2,int end) {
        int len1 = start2 - start;
        int[] tmp = new int[len1];
        System.arraycopy(array,start,tmp,0,len1);
        int p1 = 0;
        int p2 = start2;
        for(int i = start;i <= end;i++) {
            if(tmp[p1] <= array[p2]) {
                array[i] = tmp[p1];
                p1++;
                if(p1 == len1) {
                    break;
                }
            }else {
                array[i] = array[p2];
                p2++;
                if(p2 > end){
                    while(p1 < len1){
                        i++;
                        array[i] = tmp[p1];
                        p1++;
                    }
                }
            }
        }
    }
}