Chapter 10 Stability and Frequency Compensation

Chapter 8介绍了负反馈, 这一章介绍稳定性, 如果设计不好, 负反馈系统是要发生震荡的.

首先我们学习理解稳定判断标准和条件, 然后学习频率补偿, 介绍适用于不同运放的补偿方式, 同时介绍不同补偿对两级运放slew rate的影响, 最后介绍Nyquist’s判断标准

10.1 General Considerations

对于一个负反馈系统
$$\frac{Y}{X}(s)=\frac{H(s)}{1+\beta H(s)}$$

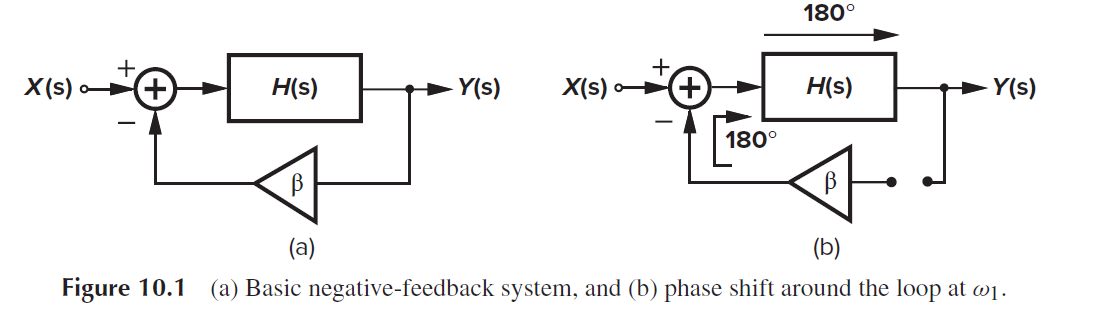
根据环路 loop gain的bode plot, phase=-180 deg时的gain可以判断系统是否稳定, 即Gain_dB<0 at Phase= -180deg, 负反馈系统稳定. 这个gain的负值即Gain Margin

也可以环路 loop gain的bode plot, gain=1时 phase 距离-180 deg 判断系统是否稳定, 即Phase 距离 -180deg >0 at Gain = 0dB, 负反馈系统稳定. 这个phase和-180的距离即Phase Margin.

Gain=1 时的频率即 unity-gain bandwidth, GBW

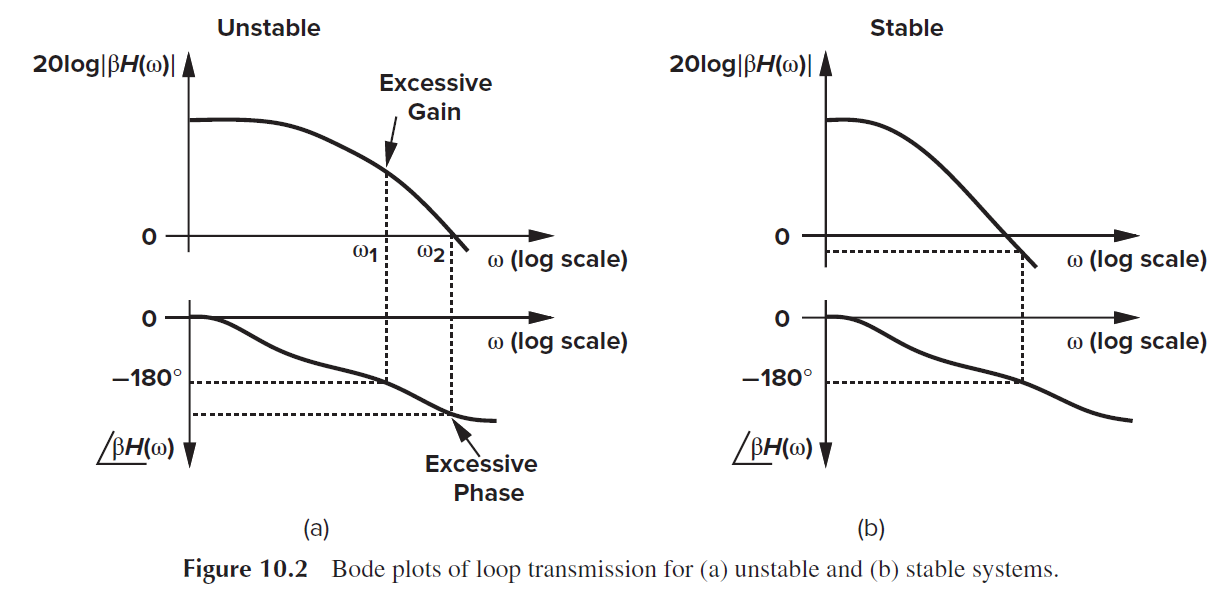
一般来说 beta越小, loop gain越小, 闭环系统越倾向稳定. 最难稳定的是unity gain feedback, 即beta=1.

对于bode plot, gain magnitude 遇到zero(wz), 在wz处以 +20 dB/dec 上升, 遇到pole(wp), wp处以 -20 dB/dec 下降.

phase 遇到zero(wz), 在0.1wz时上升, 在wz点处+45 deg, 在10wz处加到+90deg. 遇到pole (wp), 在0.1wp时下降, 在wp点处-45 deg, 在10wp处下降-90deg.

对于RHP右零点或者右极点, gain上升/下降不变, 但是phase变化相反. 需要避免右极点, 会出现震荡. 如果出现右零点要想办法补偿.

10.2 Multipole Systems

对于多极点系统, 每个pole引入-90 deg, 在wp2处引入-135 deg phase下降. 为了增加phase margin, 可以减小feedback的gain, 这样unity gain bandwidth减小.

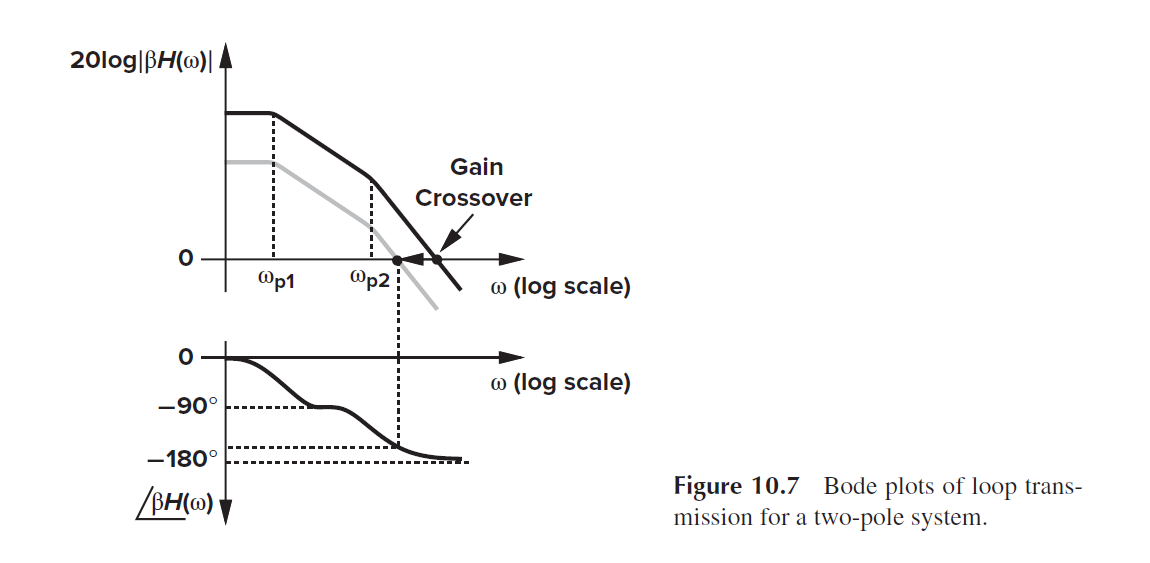
10.3 Phase Margin

Phase Margin 相位裕度就是当Gain=1时, Phase离 -180 deg的距离. 一般取PM为至少45 deg, 系统才稳定.

10.4 Basic Frequency Compensation

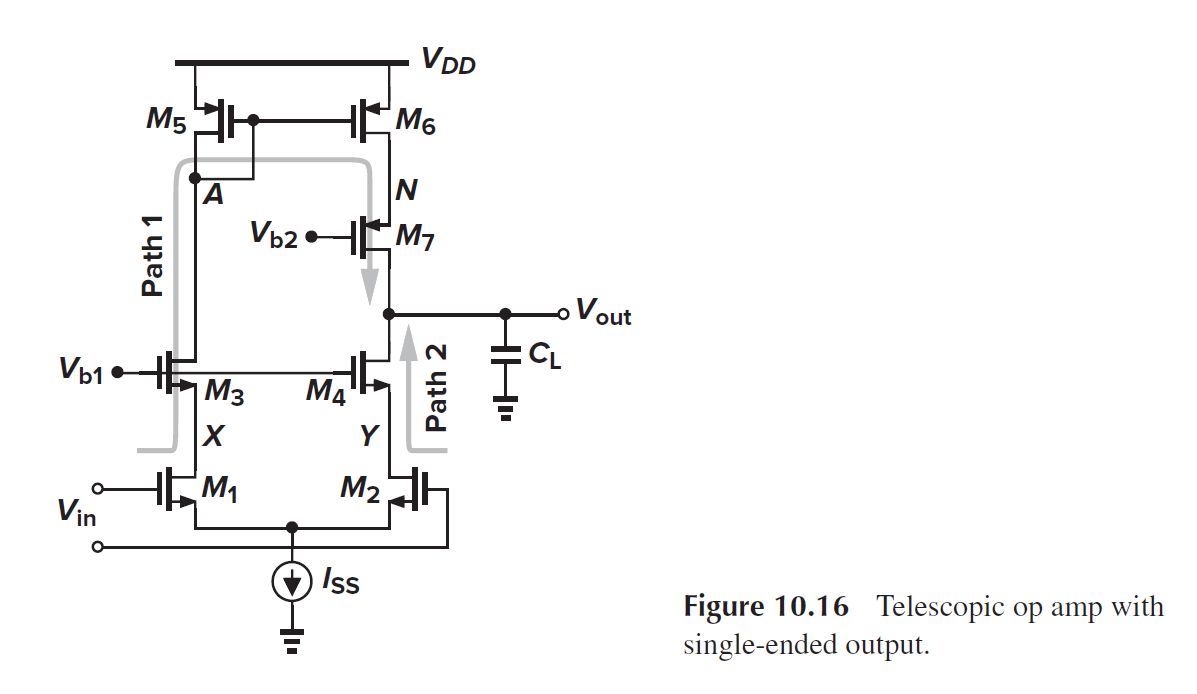
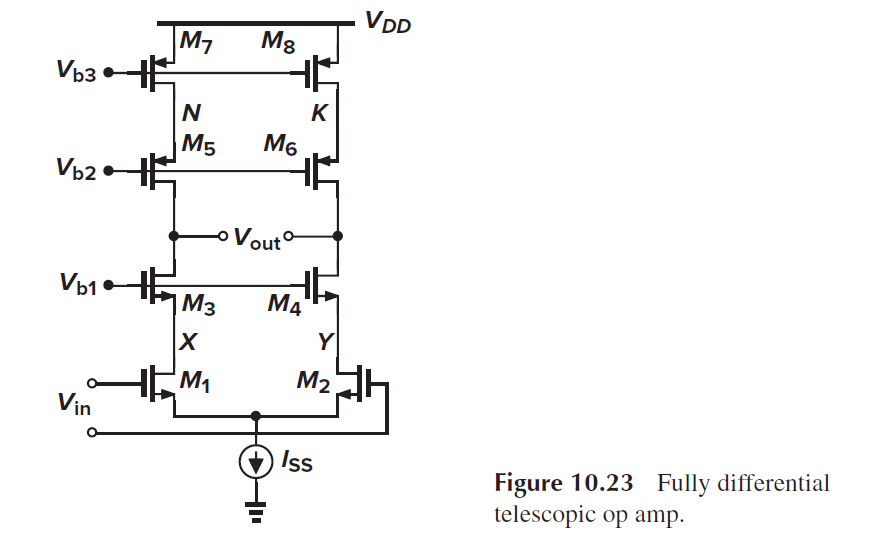
对于上面Telescopic Op结构, 主极点在Vout处, pole=1/(Rout*CL). 次极点在A处, pole=gm5/CA. 第三极点在N处pole=gm7/CN, 然后是X和Y处

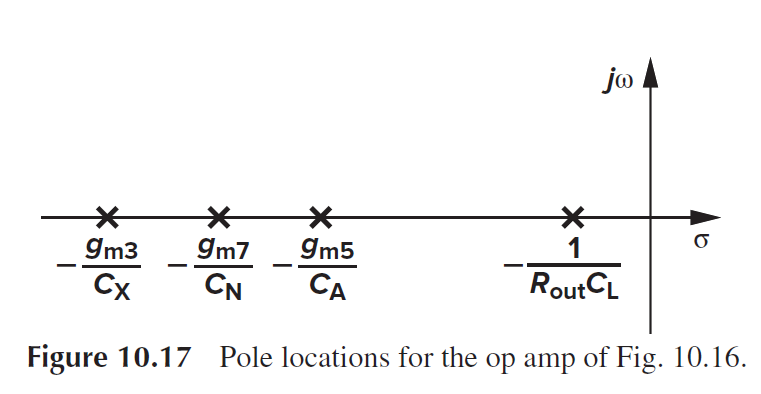
补偿手段

简单有效的补偿手段是降低主极点(把主极点往原点移), 这样通过降unity gain bandwidth的手段就可以提高Phase Margin了.

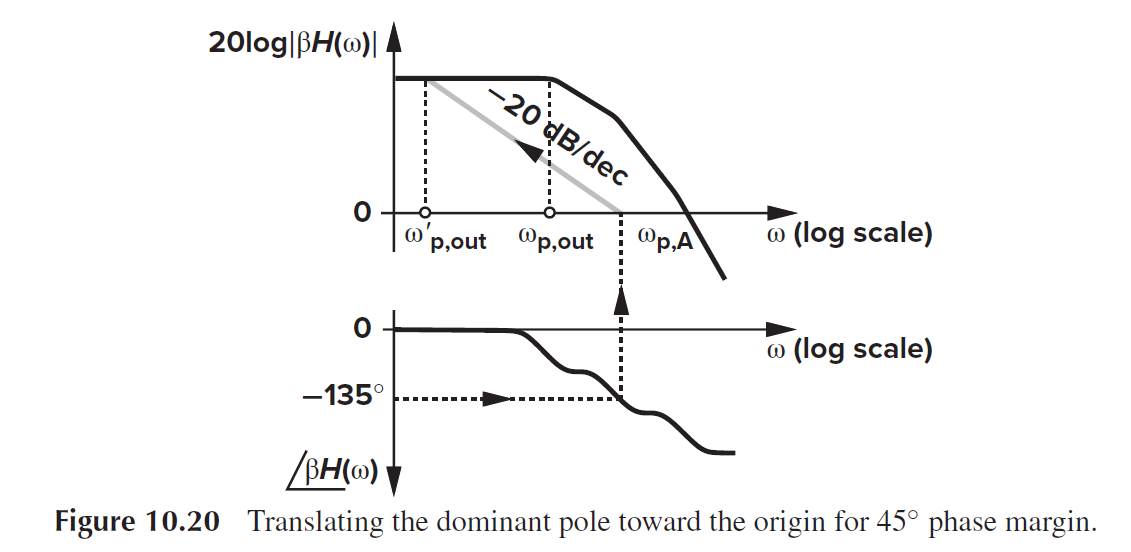
把unity gain bandwidth放在次极点, 就可以达到45 PM了.

注意: 增加Rout并不能补偿运放, 因为增加Rout会导致低频增益更高, 不改变unity gain bandwidth. 另外把非主极点挪向原点也不增加相位裕度.

对于telescopic全差分运放, N和K处的极点融入到输出极点, 不再产生额外的极点的. 相比于单端运放结构, 全差分结构只有一个次极点在X和Y处, 没有单端运放的A处次极点.

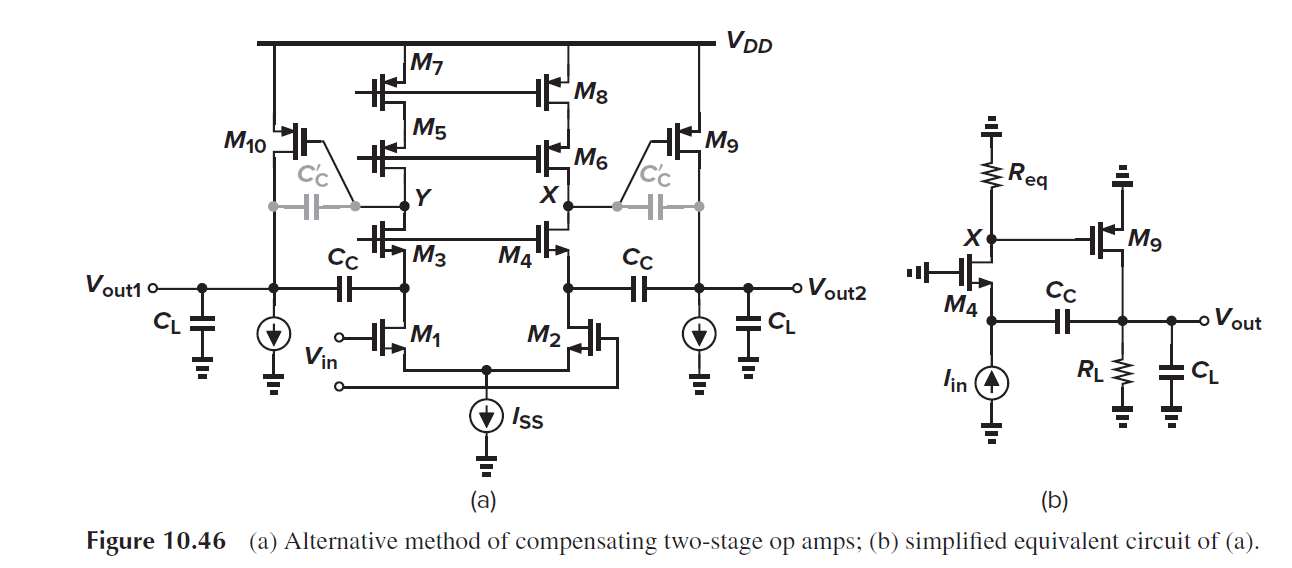
10.5 Compensation of Two-Stage Op Amps

全摆幅输出的场景需要用到两级运放, 这一节我们研究两级运放的稳定性和补偿.

我们看到三处极点: X(Y), E(F)和A(B). 上面已讨论X处的极点很高(gm3/Cx). E处的阻抗很大, 极点位置较小, A处的阻抗较小, 但CL大, 极点位置也较小. 因此有两个主极点.

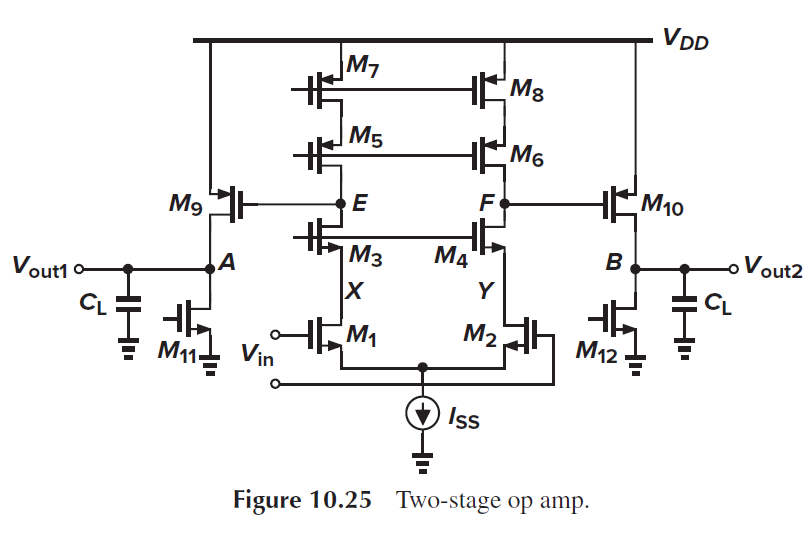
我们希望能让E这个极点更靠近原点, A这个极点更远离原点. 需要极点分离. 这样补偿后的unity gain bandwidth处于次极点A处, 不会太低.

方法就是用米勒补偿, 在M9的gate和drain之间添加电容Cc. 能增大(往外推)A点处的极点gm9*RL倍, 成为次极点 w2=gm9/CL. 因为Cc提供了在高频下E到A的通路, 减小了A处的阻抗, 从RL->1/gm9.

同时把**E处极点减小(往里推)*为1/ (AvM9 Cc * Re), 成为主极点.

米勒补偿会引入右零点, 位置wz=gm9/Cc. 右零点导致Phase下降, 但是gain上升, 因此更加恶化稳定性.

可以在Cc串联电阻Rz来消除右零点, 如下图所示

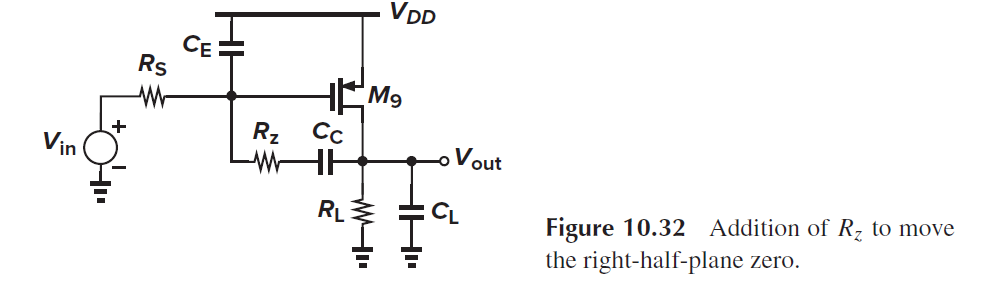
可以取Rz=1/gm9, 来消除右零点.

或者把Rz取得更大, 和次极点 w2=gm9/CL 相互抵消. 但是Rz容易受到PVT波动.

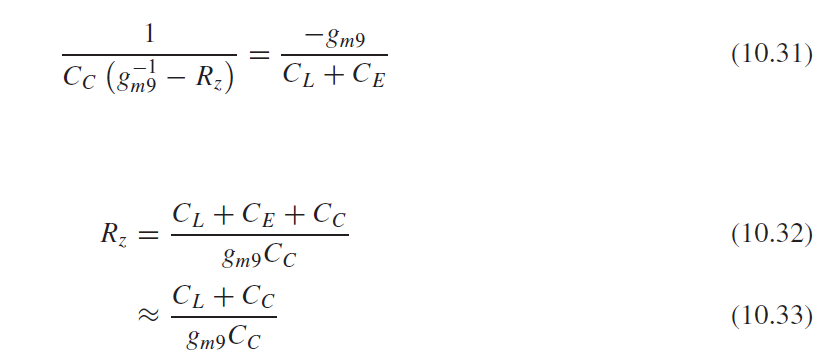
在实际生产中, Rz是由MOS进入线性区做成的, 偏差值较大. 而且零极点太靠近容易形成零极对 doublet 问题, 影响大信号step响应.

为了bias 线性区M15的Gate, 可采用下图结构. 其中I1=I9, 因此Vsg13=Vsg9, Vsg14=Vsg15, Ron15和Vgs-Vth成反比, 因此 Ron15=(W/L)14 / (W/L)15 /gm14

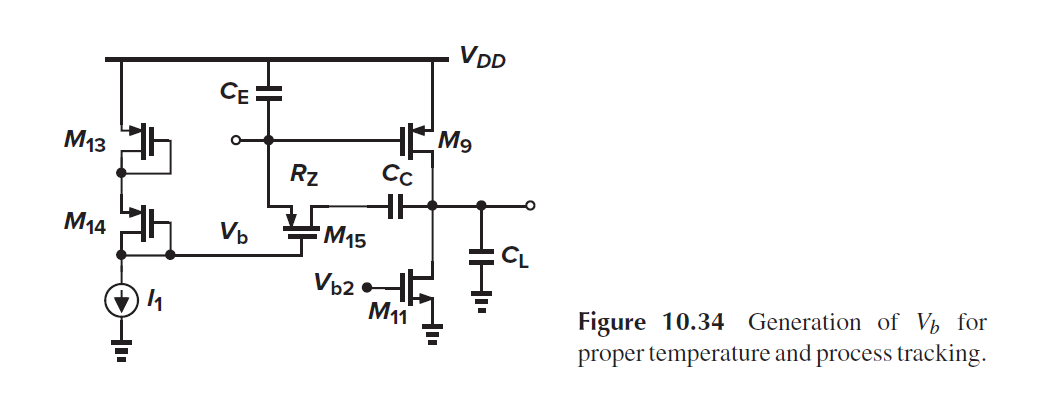
可定M15的尺寸

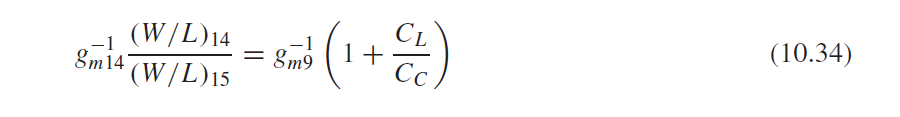
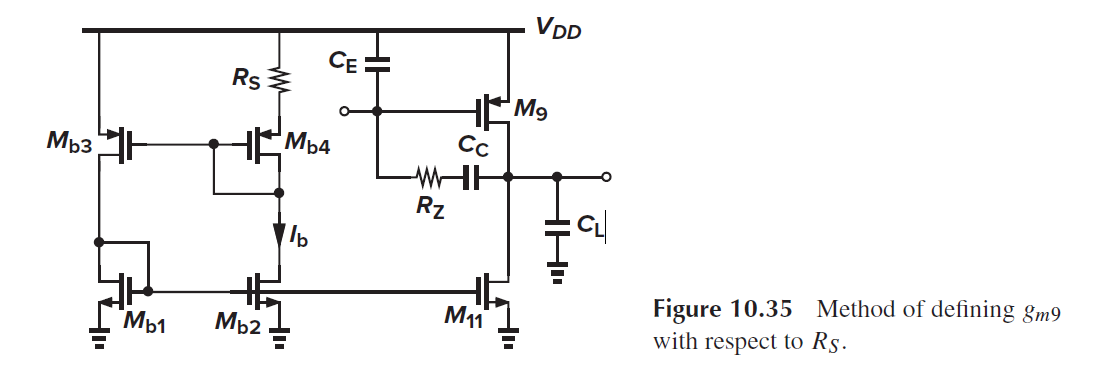
还有一种方法直接用电阻Rz, 但是gm9的电流采用Beta-Multiplier Reference, 即Ib ∝ RS^-2, gm9∝sqrt(ID9)∝ RS^-1. 因此Rz和Rs的比例保持固定, 不太受到PVT变化

需注意: 两级运放稳定性受输出电容的影响. 由于miller效应, 主极点在第一级的输出, 次极点在输出端. 如果输出电容过大, 次极点会靠近主极点, 造成Phase Margin下降. 而对于单极运放, 输出电容增大只会减小主极点, 增加Phase Margin.

Miller补偿更好的方式是Indirect feedback 或者ahuja补偿方法 **将Cc接到low-impedance node, 而不是像传统的miller补偿两级运放接到high-impedance node. **

Indirect feedback的速度更快, 面积更小, PSRR更好, 因此对于miller补偿电路, 我们都会采用Indirect feedback. 在实际中我们永远避免把补偿电容接到高阻节点!

注意: indirect feedback的接法很灵活, 关键是确保Cc反馈点和第二级的gate同一方向变化.

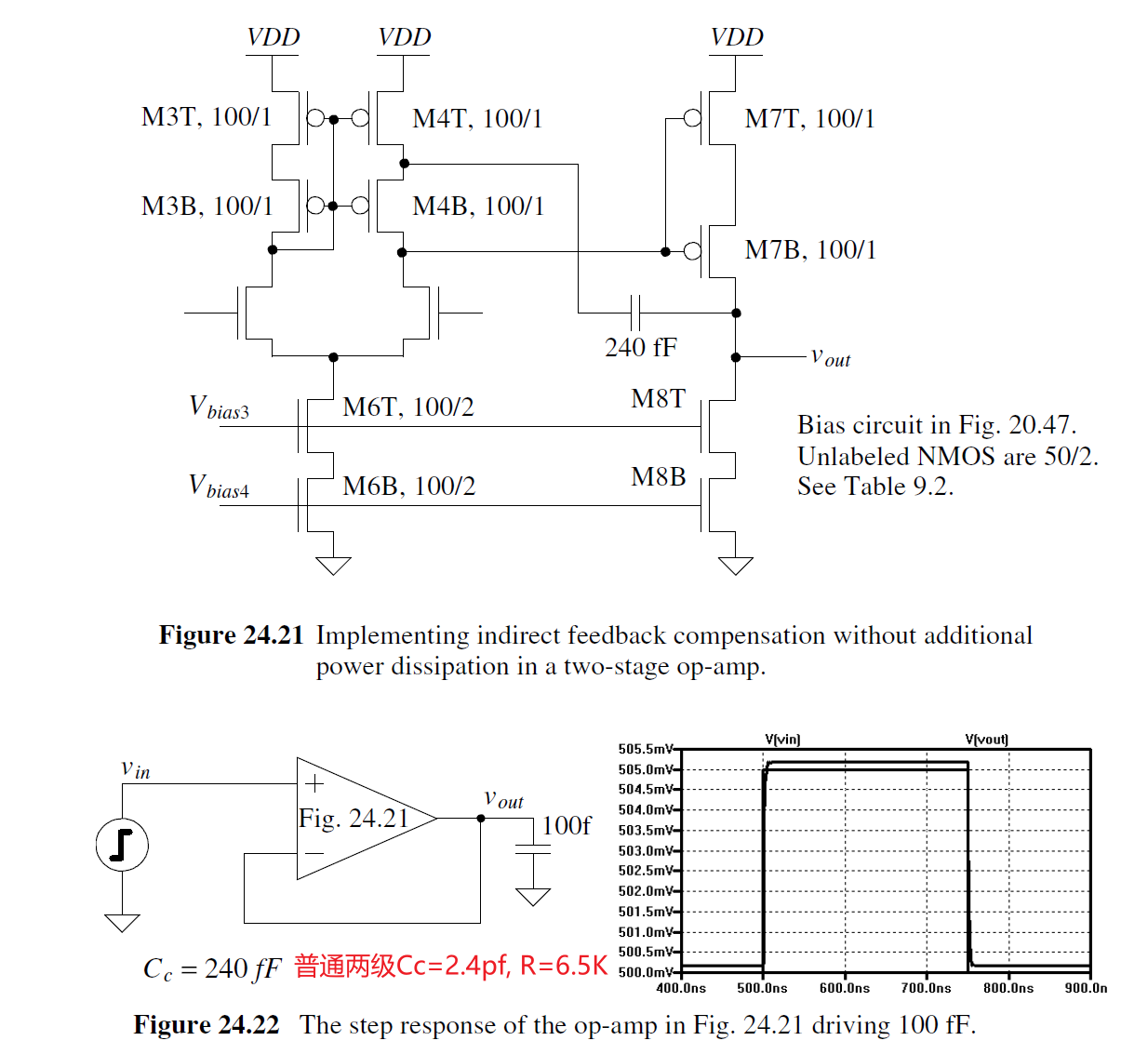
10.6 Slewing in Two-Stage Op Amps

对于miller补偿的两级运放, 由于右零点, Vin发生上升阶跃, Vout会先下降, 再上升.

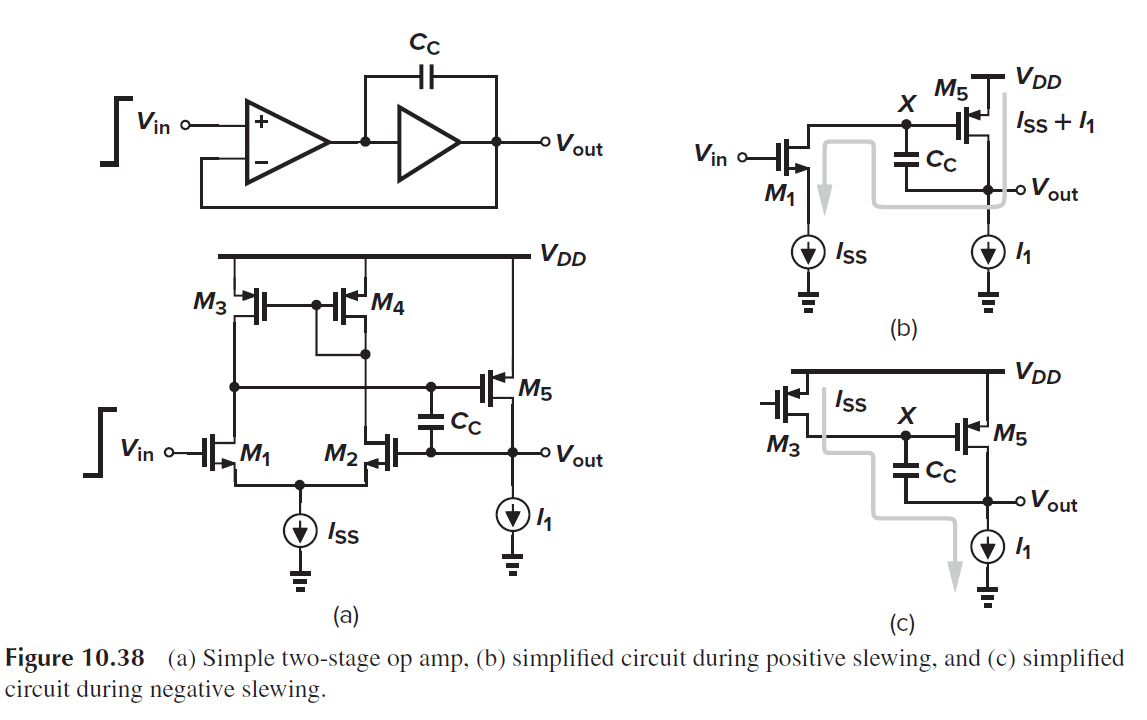
对于两级class-AB运放, 由于电流镜引入额外的极点, 降低了phase margin, 因此两级class-AB运放比class-A运放要慢

10.7 Other Compensation Techniques

对于miller补偿, 如果流过Cc电流能从Vout到X点, 而不能从X点到Vout点, 那么我们就可以把右零点推到非常高的频率位置. 我们可以加入M2 source follower, 以实现这个功能.

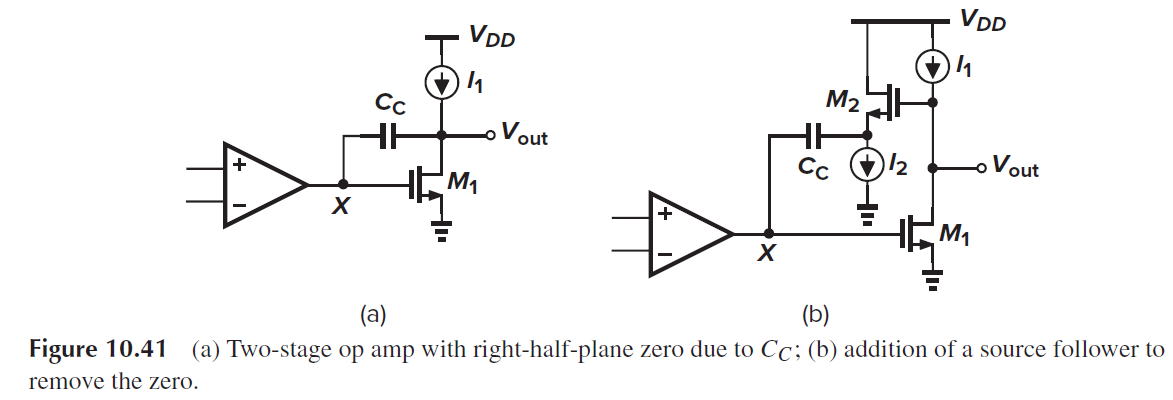
推导传输函数可得

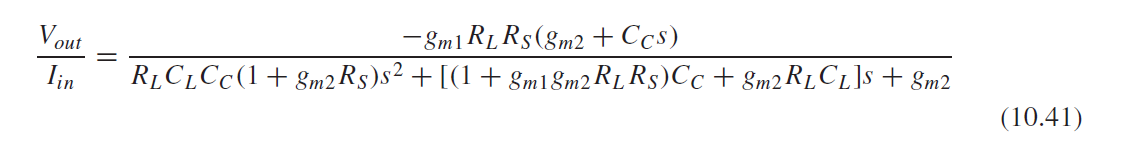
两个极点为

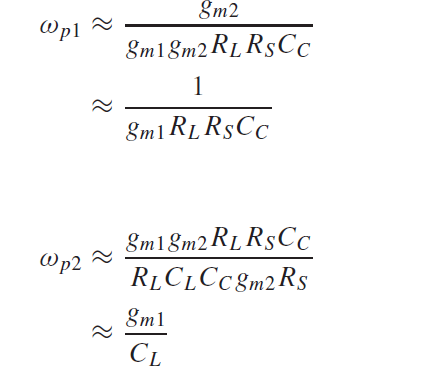
输出极点从1/(RL*CL) -> gm1/CL

source follower的问题是限制了输出Vout最低电压为Vgs2+VI2. 因此可用补偿电容Cc来隔离反馈端和输出Vout. 如下图所示. Cc和common-gate的M2将Vout转化为电流, 送到M1.

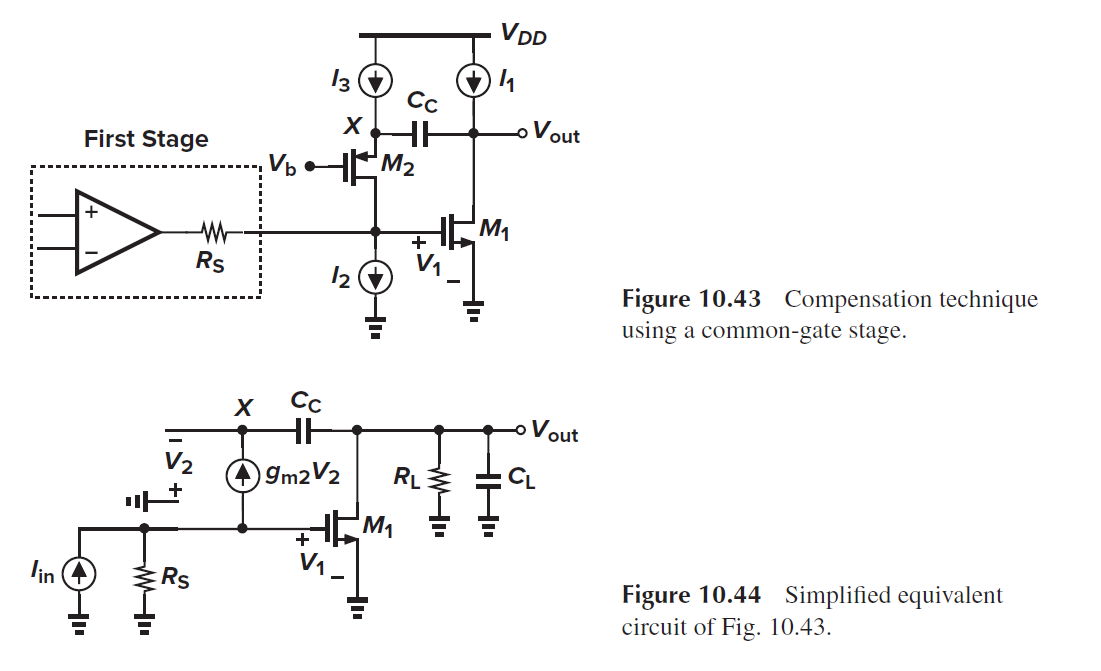
可得传输函数

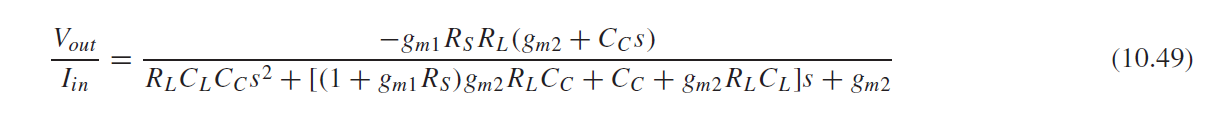
两个极点位置为

注意, 第二极点幅度增加了, 即推远了, 这是因为在高频时M2和Rs降低了输出阻抗.

另外要注意10.43结构的slew rate.

对于cascode结构, 可用下图方法. Cc连接输出极点和cascode的source端口! Req为gm*ro^2.

推导可得零点大幅增加到gm4*Req gm9/Cc. 变化前为gm9/Cc.

主极点为1/(Reqgm9RLCc). 次极点为gm4gm9Req/CL

10.8 Nyquist’s Stability Criterion