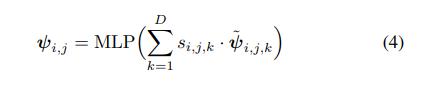操作环境：

MATLAB 2022a

1、算法描述

胡桃夹子优化算法（Nutcracker Optimization Algorithm, NOA）是一个灵感来源于胡桃夹子的故事的元启发式优化算法。这个故事中，胡桃夹子是一个能够将坚果壳轻易地破开以获取内部果仁的工具。在优化算法的语境下，这个过程被比喻为寻找问题解决方案的过程，即如何有效地“破开”问题的“坚硬外壳”以到达其核心或最优解。

灵感来源与算法理念
胡桃夹子优化算法（NOA）源自于传统的胡桃夹子工具，它通过一个简单但有效的机制破开坚硬的坚果壳以获取内部的果仁。这一过程需要精确的力度控制和对坚果特性的理解，以确保果仁完整而壳则被破开。将此过程抽象化后，NOA算法通过模拟胡桃夹子的精准力度控制和目标定位能力，来解决优化问题。算法旨在通过探索（Exploration）和利用（Exploitation）两个阶段的动态平衡，高效地导向最优解。

探索阶段的深入分析
在探索阶段，NOA算法模拟胡桃夹子寻找坚果的行为，以随机或半随机的方式在解空间中广泛搜索，寻找可能的有利区域。此阶段的目标是最大化搜索范围，确保不遗漏任何可能的最优解区域。算法采用多点搜索策略，通过生成大量随机解，并评估这些解的质量，来发现解空间中的有利区域。此外，探索阶段还引入了多样性保持机制，确保搜索过程不会过早地聚焦于局部区域，从而忽视其他潜在的最优解区域。

利用阶段的详细描绘
进入利用阶段后，NOA算法开始模仿胡桃夹子破开坚果壳的过程，通过更加集中和细致的搜索，在已识别的有利区域内寻找最优解。这一阶段关键在于算法如何在保证搜索效率的同时，精细调整搜索策略以接近全局最优解。为此，算法采用了梯度下降、局部搜索等技术，结合问题特性进行参数的动态调整。利用阶段的搜索不仅是对解的局部改进，而且通过对搜索方向和步长的智能调整，使得搜索过程能够在全局最优解的方向上持续进展。

适应性调整机制
NOA算法的一个核心特点是其适应性调整机制，该机制能够根据当前搜索过程的表现动态调整探索与利用之间的平衡。这一机制的设计灵感来源于胡桃夹子根据不同坚果的特性（如硬度和大小）调整施力的能力。在算法中，这种调整通过实时监测搜索过程中解的质量变化来实现。如果发现解的改进速率放缓，表明可能已经接近局部最优解，算法会增加探索力度，寻找新的有利区域；相反，如果在某一区域内连续获得解的显著改进，算法则增强利用策略，以精确逼近最优解。

算法流程的详细说明
NOA统的胡桃夹子故事和工具，这一点提供了算法设计的初步灵感。在故事中，胡桃夹子能够有效地破开坚果壳，揭示出内部的果仁。将这一过程抽象化，我们可以将其视为一种解决问题的策略：即通过有效的策略“破开”问题的复杂“外壳”，以揭示和接近问题的核心或最优解。

这一灵感转化为算法设计中的两个关键概念：探索（Exploration）和利用（Exploitation）。探索相当于在广阔的解空间中寻找有前景的“坚果”，即潜在的好解；而利用则相当于对找到的“坚果”施加压力，破开壳子获取果仁，即精细调整解向最优解靠拢。

算法组件详述
探索阶段
在探索阶段，算法通过随机或半随机的策略在解空间内广泛搜索，目的是为了发现可能包含最优解的区域。这个过程类似于在一片广阔的森林中寻找可能含有珍贵果仁的坚果。为了有效执行这一任务，算法采用多点搜索策略，同时从多个位置出发，以增加发现有价值区域的概率。

此外，探索阶段也会引入一定的随机扰动，以避免算法过早地聚焦于某个可能的局部最优区域，从而忽略了其他潜在的更优解区域。这种扰动可以通过改变搜索方向、调整搜索步长等方式实现。

利用阶段
一旦在探索阶段发现了有潜力的解区域，算法随即进入利用阶段。在这一阶段，算法将更加集中精力在这些有前景的区域进行深入搜索。这类似于已经找到坚果，并专注于如何有效地破开壳子获取里面的果仁。

利用阶段的关键在于如何精细调整搜索策略，以确保能够有效逼近最优解。这通常涉及到减小搜索步长、细化搜索方向等方法。此外，算法还会根据当前搜索结果的反馈动态调整搜索策略，以实现对最优解的精确定位。

适应性调整
胡桃夹子优化算法的一个显著特点是其适应性。算法能够根据当前的搜索进展和解的质量自动调整探索与利用之间的平衡。这种适应性调整确保了算法在搜索过程中既不会因过度探索而漫无目的，也不会因过度利用而陷入局部最优。

适应性调整的实现通常依赖于一个反馈机制，通过评估当前解集的多样性、改进速率等指标来动态调整探索和利用的强度。例如，如果算法发现解的改进速率下降，可能会增加探索的比重，以寻找新的有潜力的区域。

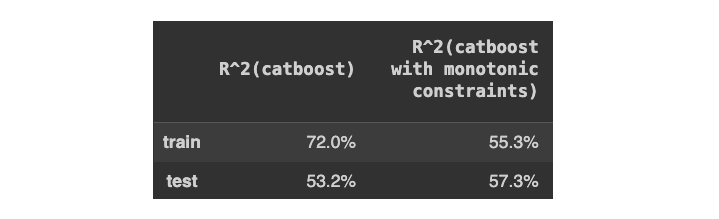
2、仿真结果演示

3、关键代码展示

略

4、MATLAB 源码获取

点击下方原文链接获取

【MATLAB源码-第160期】基于matlab的胡桃夹子优化算法（NOA）无人机三维路径规划，输出做短路径图和适应度曲线-CSDN博客https://blog.csdn.net/Koukesuki/article/details/136615000?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522D71FE990-D79C-457A-A966-8498D8AEFF8F%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=D71FE990-D79C-457A-A966-8498D8AEFF8F&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-136615000-null-null.nonecase&utm_term=160&spm=1018.2226.3001.4450