0. 简介
《WidthFormer: Toward Efficient Transformer-based BEV View Transformation》提出了WidthFormer,这是一种基于Transformer的新颖鸟瞰视角(Bird's-Eye-View, BEV)三维检测方法,专为实时自动驾驶应用而设计。WidthFormer在计算上高效、稳健,且无需特殊的工程努力即可部署。我们提出了一种新颖的三维位置编码机制,能够准确地封装三维几何信息,使得我们的模型仅通过一个Transformer解码层就能生成高质量的BEV表示。这种机制对现有的稀疏三维对象检测器也是有益的。受到最近提出的工作的启发,我们进一步通过垂直压缩图像特征(作为注意力键和值)来提高模型的效率。我们还引入了两个模块,以补偿由于特征压缩而可能导致的信息损失。在广泛使用的nuScenes三维对象检测基准上的实验评估表明,我们的方法在不同的三维检测架构上均优于以往的方法。更重要的是,我们的模型高度高效。例如,在使用256×704输入图像时,它在NVIDIA 3090 GPU和Horizon Journey-5计算解决方案上实现了1.5毫秒和2.8毫秒的延迟。此外,WidthFormer还展示了对不同程度的摄像机扰动的强大鲁棒性。我们的研究为BEV变换方法在真实世界复杂道路环境中的部署提供了宝贵的见解。代码可在 GitHub - ChenhongyiYang/WidthFormer: [IROS 2024 Oral Presentation] WidthFormer: Toward Efficient Transformer-based BEV View Transformation 获取。
1. 主要贡献
本文提出了以下四个贡献:
- 我们引入了WidthFormer,这是一种轻量级且适合部署的BEV转换方法,它使用一个Transformer解码器层来计算BEV表示。
- 我们提出了参考位置编码(RefPE),这是一种新的位置编码机制,用于3D物体检测,可以帮助WidthFormer辅助WidthFormer的视角转换。它还可以以即插即用的方式提高稀疏3D物体检测器的性能。
- 我们在广泛使用的nuScenes 3D物体检测数据集上评估了所提出的模块。结果显示,RefPE可以显著提高稀疏物体检测器的性能。
- 此外,WidthFormer在一系列3D检测架构中在性能和效率上均优于先前的BEV转换方法。
<br/>
2. 主要方法
在这一节中,我们将详细介绍我们的方法。首先,在第3节中,我们引入了新的3D位置编码机制。接着,在第4节中,我们介绍了我们的BEV转换模块。在第5节中,我们描述了如何对潜在的信息损失进行压缩特征的优化处理。
3. 参考位置编码(RefPE)
在这项工作中,我们为基于Transformer的3D物体检测器(例如PETR [20])以及我们的BEV视图转换模块设计了一种新的3D位置编码机制。直观地说,对于每个在Transformer中作为键和值的视觉特征,我们的目标是通过参考一系列参考点来学习其位置编码;因此,我们将我们的方法称为参考位置编码(RefPE)。给定多视角图像特征FI∈RNc×HI×WI×CFI∈RNc×HI×WI×C,其中NcNc是摄像头数量;HIHI,WIWI和CC分别是高度、宽度和通道维度,计算得到的位置编码与输入特征具有相同的形状。具体来说,对于一个特征像素,其在图像平面上的坐标为Pi,j=[ui,j,vi,j]⊤Pi,j=[ui,j,vi,j]⊤,我们首先将该像素与DD 个离散深度分档关联起来,从而产生DD个参考点,其齐次坐标为{P^i,j,k=[ui,j×dk,vi,j×dk,dk]⊤∣k∈∣D∣}{P^i,j,k=[ui,j×dk,vi,j×dk,dk]⊤∣k∈∣D∣},然后我们通过投影将所有这些D个点映射到一个统一的3D空间中:
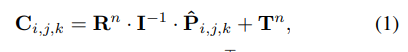
给定三维点的笛卡尔坐标Ci,j,k=[xi,j,k,yi,j,k,zi,j,k]⊤Ci,j,k=[xi,j,k,yi,j,k,zi,j,k]⊤;矩阵I∈R3×3I∈R3×3为相机内参矩阵;矩阵Rn∈R3×3Rn∈R3×3和向量Tn∈R3×1Tn∈R3×1是将第n个视角中的坐标变换到统一的激光雷达坐标系的旋转矩阵和平移向量 [1, 7]。
然后,我们使用极坐标来计算位置编码,其中自车位于原点:每个三维点的位置信息被编码为三个部分的组合:1) 相对于BEV平面上的自车的距离,2) 相对于BEV平面上的自车的旋转角度,以及3) 相对于地面的高度。具体地,对于二维点Pi,jPi,j和其参考点集合{Ci,j,k∣k∈∣D∣}{Ci,j,k∣k∈∣D∣},我们首先计算了所有参考点{ψˉi,j,k}{ψˉi,j,k}的位置编码:
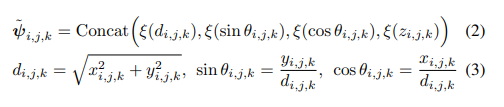
在这里,ξ代表的是傅里叶位置编码 [30]。接下来,通过使用一系列的参考系数和多层感知器(MLP),我们来计算Pi,jPi,j的值,将{ψˉi,j,k}{ψˉi,j,k}进行聚合:
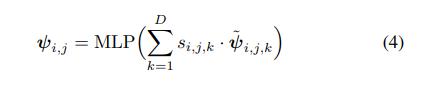
在这里,参考系数{s∗,∗,k}{s∗,∗,k}是由一个轻量级卷积头部预测的。
点击经典文献阅读之--WidthFormer(基于Transformer的BEV方案量产方案) ——古月居可查看全文