k-nearest neighbors(KNN)算法是监督机器学习中最简单但最常用的算法之一。
KNN通常被认为是一种惰性的学习算法,从技术上讲,它只是存储训练数据集,而不经历训练阶段。
KNN的原理是将新样本的特征与数据集中现有样本的特征进行比较。然后通过算法选择最接近的k个样本(k是自定义参数),新样本的输出是基于"k"最近样本的多数类(用于分类)或平均值(用于回归)确定的。
机器学习算法可以分为参数模型和非参数模型:
参数模型:估计训练数据集中的参数,学习可以对新数据点进行分类的函数,而不再需要原始训练数据集。典型模型有感知器、逻辑回归和线性 SVM。
非参数模型不能用一组固定的参数来表征,参数的数量随着训练数据量的变化而变化。典型的模型有决策树分类器/随机森林、SVM、KNN。
KNN在分类问题中应用更加广泛,但也可以应用于回归问题。
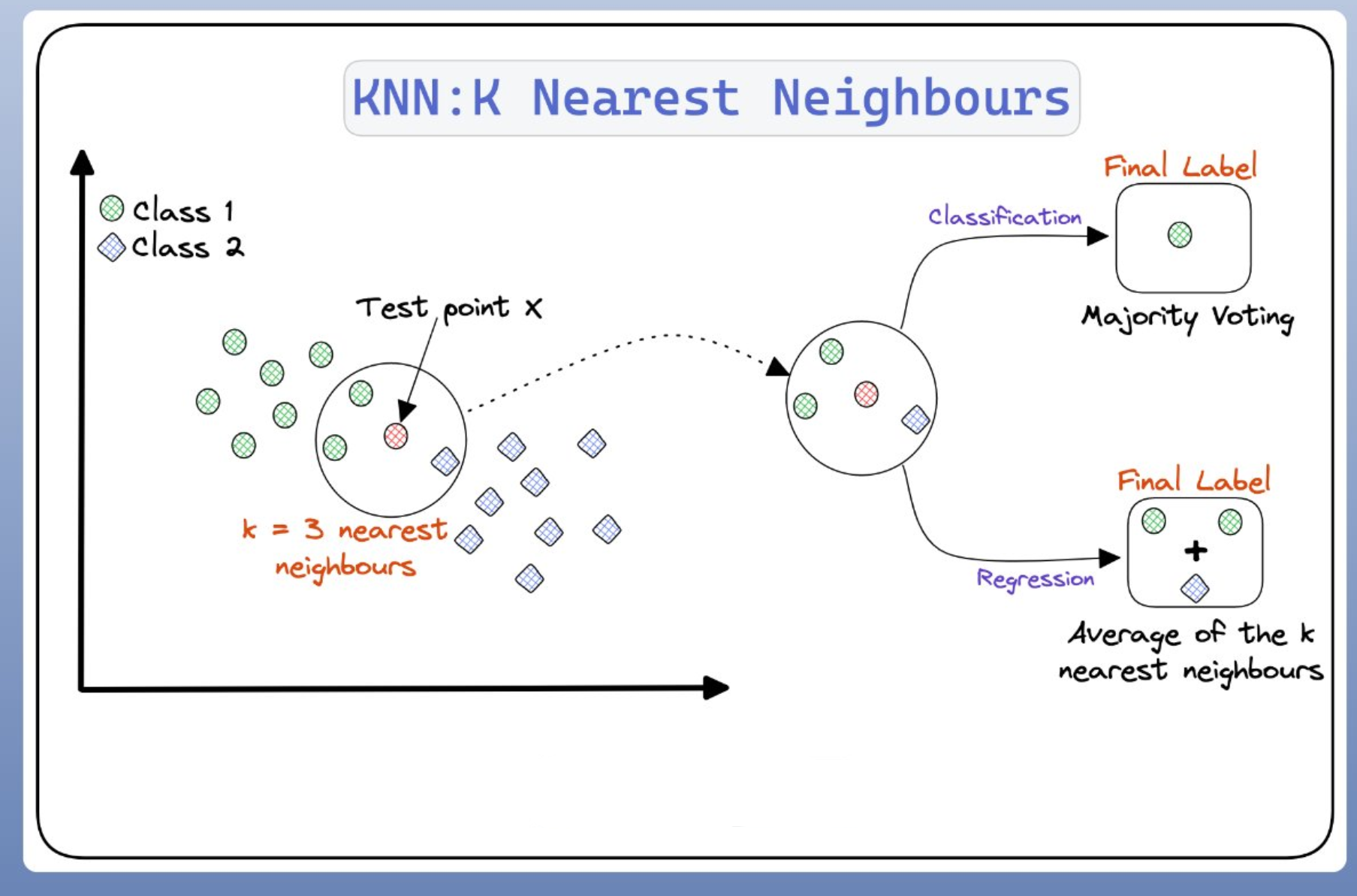
KNN 算法本身相当简单,可以概括为以下步骤:
-
选择k的值和距离度量
-
根据计算的距离,选择最近的K个邻近点
-
分类:根据选定邻近点中不同类别的比例来决定测试样本的类别。
回归:根据选定邻近点的平均值(或基于距离的加权平均),作为测试样本的预测值。
寻找观测值的最近邻
k近邻算法 (KNN) 的目标是识别给定测试点的最近邻,以便我们可以为该点分配一个类标签,因此确定距离的度量方法有助于形成决策边界,而决策边界可将测试点划分为不同的区域
要找到一个观测值的 k 个最近的观测值(邻居),可以使用 scikit-learn 的NearestNeighbors类,scikit-learn 提供了多种距离度量方法,默认情况下,NearestNeighbors使用闵可夫斯基距离(Minkowski distance)距离:
d m i n k o w s k i = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p d_{minkowski}=\left(\sum\limits_{i=1}^n\left|x_i-y_i\right|^p\right)^{1/p} dminkowski=(i=1∑n∣xi−yi∣p)1/p
其中,xi 和 yi 是我们正在计算距离的两个值。
实际上,闵可夫斯基距离 (Minkowski Distance)是将多种距离公式(曼哈顿距离、欧式距离、切比雪夫距离)的一个推广。
当闵可夫斯基距离的超参数 p = 1时为曼哈顿距离(Manhattan distance):
d m a n h a t t a n = ∑ i = 1 n ∣ x i − y i ∣ d_{manhattan}=\sum_{i = 1}^n|x_i-y_i| dmanhattan=i=1∑n∣xi−yi∣
当p = 2 时为欧几里得距离(Euclidean distance):
d e u c l i d e a n = ∑ i = 1 n ( x i − y i ) 2 d_{euclidean}=\sqrt{\sum_{i=1}^n\left(x_i-y_i\right)^2} deuclidean=i=1∑n(xi−yi)2
默认情况下,scikit-learn 中 p = 2。
下面基于鸢尾花数据集,使用NearestNeighbors来找到新建观测值new_observation在标准化特征空间中距离最近的两个点:
# Load libraries
from sklearn import datasets
from sklearn.neighbors import NearestNeighbors
from sklearn.preprocessing import StandardScaler
# Load data
iris = datasets.load_iris()
features = iris.data
# Create standardizer
standardizer = StandardScaler()
# Standardize features
features_standardized = standardizer.fit_transform(features)
# Two nearest neighbors
nearest_neighbors = NearestNeighbors(n_neighbors=2).fit(features_standardized)
# Create an observation
new_observation = [ 1, 1, 1, 1]
# Find distances and indices of the observation's nearest neighbors
distances, indices = nearest_neighbors.kneighbors([new_observation])
# View the nearest neighbors
features_standardized[indices]
# View distances
distances
还可以使用metric参数设置距离度量,例如通过metric参数将距离度量方法设为欧式距离:
# Find two nearest neighbors based on Euclidean distance
nearestneighbors_euclidean = NearestNeighbors( n_neighbors=2, metric='euclidean').fit(features_standardized)
p参数与metric参数都可以用于设置距离度量方法,区别在于p参数用于指定Minkowski距离的阶数,因此只有当metric='minkowski'时才生效,其他情况下p参数会被忽略。
此外,我们可以使用kneighbors_graph创建一个矩阵来指示每个观测值的最近邻:
# Find each observation's three nearest neighbors
# based on Euclidean distance (including itself)
nearestneighbors_euclidean = NearestNeighbors( n_neighbors=3, metric="euclidean").fit(features_standardized)
# List of lists indicating each observation's three nearest neighbors
# (including itself)
nearest_neighbors_with_self = nearestneighbors_euclidean.kneighbors_graph( features_standardized).toarray()
# Remove 1s marking an observation is a nearest neighbor to itself
for i, x in enumerate(nearest_neighbors_with_self):
x[i] = 0
# View first observation's two nearest neighbors
nearest_neighbors_with_self[0]
当我们使用任何基于距离的学习算法时,转换特征以使它们处于相同的尺度非常重要。
如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要),此时需要使用 StandardScaler 标准化功能来解决这个问题。
创建KNN分类器
在 KNN 中,给定一个具有未知目标类别的观测值 xu,算法首先根据某种距离度量(例如欧几里得距离)识别 k 个最接近的观测值(有时称为 xu的邻域),然后根据这 k 个观测值的类别占比来确定未知观测值的类别。
更正式地说,某个类 j 的概率 xu是:
1 k ∑ i ∈ ν I ( y i = j ) \frac{1}{k}\sum_{i\in\nu}I(y_i=j) k1i∈ν∑I(yi=j)
其中, ν 是 xu 邻域中的第 k 个观测值,yi 是第 i 个观测值的类别,I 是指示函数(即,1 为真,否则为 0)。
在scikit-learn中,如果数据集不是很大,则使用KNeighborsClassifier创建KNN分类器:
# Load libraries
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
# Load data
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Create standardizer
standardizer = StandardScaler()
# Standardize features
X_std = standardizer.fit_transform(X)
# Train a KNN classifier with 5 neighbors
knn = KNeighborsClassifier(n_neighbors=5, n_jobs=-1, algorithm='auto').fit(X_std, y)
# Create two observations
new_observations = [[ 0.75, 0.75, 0.75, 0.75], [ 1, 1, 1, 1]]
# Predict the class of two observations
knn.predict(new_observations)
对于可以使用Predict_proba查看观测值属于不同类别的概率:
# View probability that each observation is one of three classes
knn.predict_proba(new_observations)
使用KNeighborsClassifier 需要考虑以下几个参数:
-
通过
metric参数设置使用的距离度量 -
通过
n_jobs参数确定要使用多少个计算机核心,由于进行预测需要计算数据中一个点到每个点的距离,因此建议使用多个核心。 -
通过
algorithm参数设置算法,但默认情况下会尝试自动选择最佳算法。 -
通过
weights参数设置权重,可选择uniform、distance,或是自定义函数。uniform代表邻域内邻近点的权重都是相等的;distance代表是邻域内距离近点相较于距离远的点有更高的权重;用户自定义的函数可以接收距离的数组,并返回一组维数相同的权重数组。
最后,由于距离计算将所有特征视为同一尺度,因此在使用 KNN 分类器之前很有必要对特征进行标准化(standardize)。
确定最佳邻域尺寸
k的大小对 KNN 分类器有实际影响。在机器学习中,我们都想要在偏差和方差之间找到一个平衡点,但很少能找到像 k 值这样明确的平衡点。
-
如果 k = n,其中 n 是观测值的数量,会完全根据样本数据的分布进行预测,不管新样本什么样,全部都会预测成样本数据中样本数量最多的那个类别,此时模型会呈现为:高偏差(bias)、低方差(variance)。
-
如果 k = 1,根据最相似的一个样本判断分类,预测准确的概率很高,但是不同数据集中,与新样本S相似度最高的那个样本可能属于不同分类,那么预测结果则各不相同,因此模型会呈现为:低偏差,高方差。
所以,训练最佳模型的关键是找到能平衡偏差和方差的 k 值。
这里可以使用GridSearchCV对不同 k 值的 KNN 分类器进行交叉验证:
# Load libraries
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.model_selection import GridSearchCV
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create a pipeline
pipe = Pipeline([
("standardizer", StandardScaler()),
("knn", KNeighborsClassifier(n_jobs=-1))
])
# Create space of candidate values
search_space = {"knn__n_neighbors": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}
# Create grid search
classifier = GridSearchCV( pipe, search_space, cv=5, verbose=0)
classifier.fit(features, target)
# Best neighborhood size (k)
classifier.best_estimator_.get_params()["knn__n_neighbors"]
经过5折交叉验证可以得到上述代码最佳k值为6。
创建基于半径的最近邻分类器
在 KNN 分类中,观测值的类别是根据其 k个邻近点的类别来预测的。
还有一种分类方法是基于半径的最近邻 (radius-based nearest neighbor) 分类,该方法的观测值的类别是根据给定半径 r 内的所有观测值的类别来预测的。
# Load libraries
from sklearn.neighbors import RadiusNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Create standardizer
standardizer = StandardScaler()
# Standardize features
features_standardized = standardizer.fit_transform(features)
# Train a radius neighbors classifier
rnn = RadiusNeighborsClassifier( radius=.5, n_jobs=-1).fit(features_standardized, target)
# Create two observations
new_observations = [[ 1, 1, 1, 1]]
# Predict the class of two observations
rnn.predict(new_observations)
在 scikit-learn 中,RadiusNeighborsClassifier(基于半径的最近邻分类器)与KNeighborsClassifier(k近邻分类器)非常相似,但有两个参数不同:
- 使用
RadiusNeighborsClassifier需要通过radius参数指定固定区域的半径来确定邻近点。 - 使用
RadiusNeighborsClassifier需要通过outlier_label参数指定在模型中对离群点(即在指定半径内没有邻居的点)的处理方式,默认使用数据集中最频繁的标签来处理离群点;如果指定为None,那么遇到离群点时,模型会抛出一个异常;也可以手动指定一个标签(例如0或-1),用于标记离群点。
最近邻回归器
回归和分类最要的区别就是:回归的目标数据是连续的,分类的目标数据是离散的。
KNN用于分类问题上时,用于预测离散的类别标签,通过判断K个最近观测值中各种类型的占比来确定预测值。
KNN用于回归问题上时,用于预测连续的数值,通常使用K个最近观测值的平均值或加权平均值来输出预测值。
下面的案例是使用加利福尼亚房价数据集来预测加利福尼亚各区域的房价中位数,并且分析了不同k值对模型性能的影响:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
from sklearn.inspection import permutation_importance
# Load California Housing dataset
california = fetch_california_housing()
X, y = california.data, california.target
# Standardize the features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# Function to evaluate model performance
def evaluate_model(k):
knn = KNeighborsRegressor(n_neighbors=k, n_jobs=-1)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
return knn, mse, r2
# Test different k values
k_values = range(1, 21)
mse_scores = []
r2_scores = []
for k in k_values:
_, mse, r2 = evaluate_model(k)
mse_scores.append(mse)
r2_scores.append(r2)
# Find the best k value
best_k = k_values[np.argmax(r2_scores)]
print(f"Best k value: {best_k}")
# Use the best k value for final model
best_knn, mse, r2 = evaluate_model(best_k)
y_pred = best_knn.predict(X_test)
print(f"Mean Squared Error (MSE) for best model: {mse:.2f}")
print(f"R2 Score for best model: {r2:.2f}")
# Predict a new sample
new_sample = X_test[0].reshape(1, -1)
predicted_price = best_knn.predict(new_sample)[0]
actual_price = y_test[0]
print(f"\nPredicted median house value for new sample: ${predicted_price:.2f}k")
print(f"Actual median house value for new sample: ${actual_price:.2f}k")
# 1. Visualization: Predicted vs Actual Values for the best model
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.1)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel("Actual Values")
plt.ylabel("Predicted Values")
plt.title(f"KNN Regression (k={best_k}): Predicted vs Actual Values")
plt.tight_layout()
plt.show()
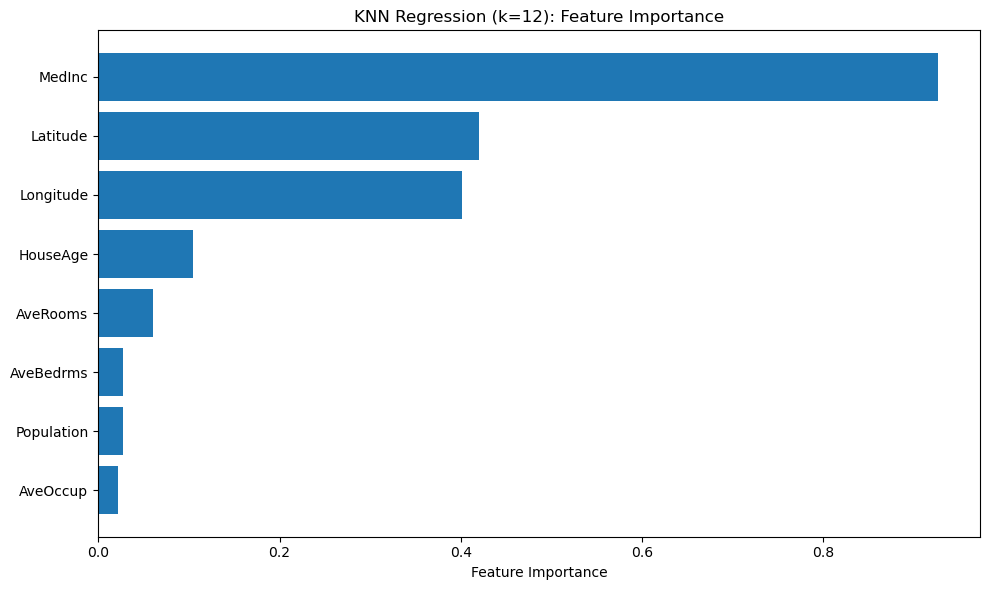
# 2. Calculate and visualize feature importance for the best model
result = permutation_importance(best_knn, X_test, y_test, n_repeats=10, random_state=42, n_jobs=-1)
importances = result.importances_mean
feature_names = california.feature_names
plt.figure(figsize=(10, 6))
sorted_idx = importances.argsort()
plt.barh(range(X.shape[1]), importances[sorted_idx])
plt.yticks(range(X.shape[1]), [feature_names[i] for i in sorted_idx])
plt.xlabel("Feature Importance")
plt.title(f"KNN Regression (k={best_k}): Feature Importance")
plt.tight_layout()
plt.show()
# 3. Visualization: Comparing different k values
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(k_values, mse_scores, 'bo-')
plt.xlabel('Number of Neighbors (k)')
plt.ylabel('Mean Squared Error')
plt.title('MSE vs. k')
plt.subplot(1, 2, 2)
plt.plot(k_values, r2_scores, 'ro-')
plt.xlabel('Number of Neighbors (k)')
plt.ylabel('R2 Score')
plt.title('R2 Score vs. k')
plt.tight_layout()
plt.show()
运行结果为:
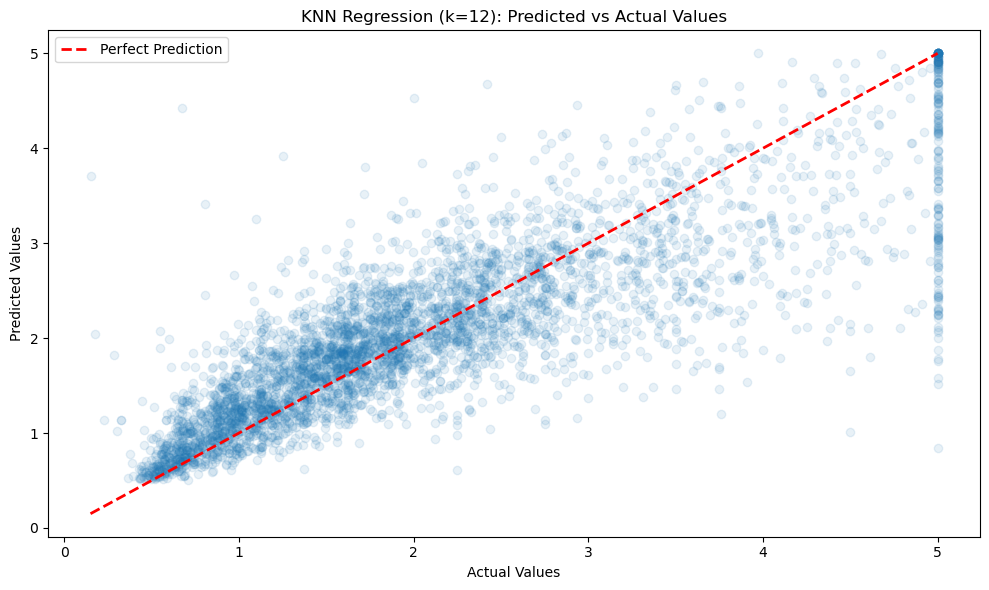
Best k value: 12
Mean Squared Error (MSE) for best model: 0.41
R2 Score for best model: 0.68
Predicted median house value for new sample: $0.55k
Actual median house value for new sample: $0.48k
比较预测值和实际值:
使用排列重要性(permutation importance)来对比不同特性的重要性:
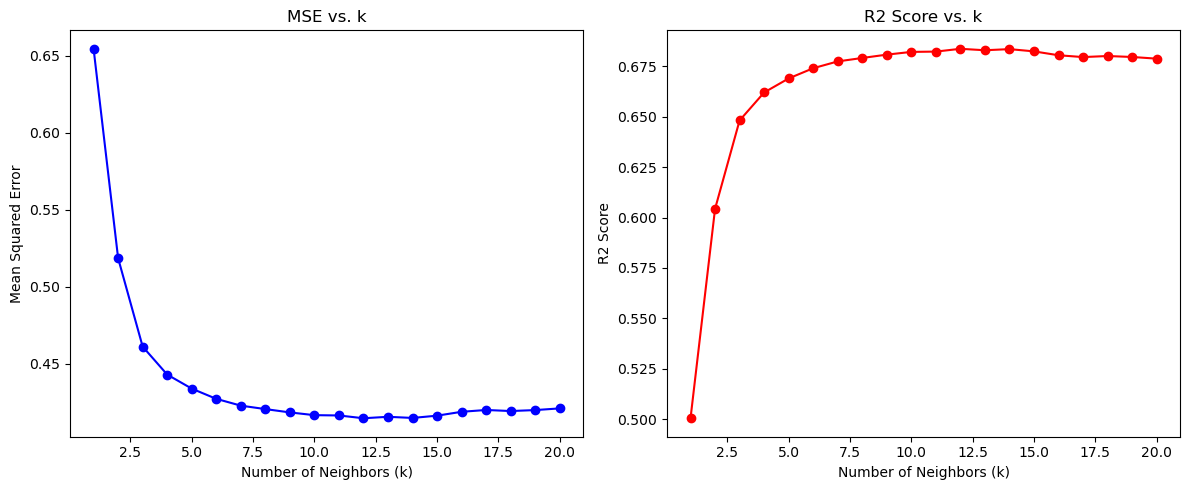
不同k值对模型性能的影响:
KNN回归对比线性回归
线性回归是一种参数方法,其假设因变量和自变量线性相关,其原理是通过最小二乘法等方式拟合一条直线,其特点为:
- 计算简单快速,易于理解和实现
- 可解释性强,系数代表特征重要性
- 对异常值较敏感
- 无法捕捉非线性关系
KNN回归是一种非参数方法,不假设数据的分布形状,适用于非线性数据,其特点为:
- 基于相似性原理,预测值由最近邻的平均值决定
- 对非线性关系表现较好
- 计算复杂度较高,尤其是大数据集
- 需要存储全部训练数据
- 对异常值较敏感
- 特征尺度敏感,通常需要归一化