目录
一、做题心得
二、题目与题解
题目一:卡码网 101. 孤岛的总面积
题目链接
题解:DFS
题目二:卡码网 102. 沉没孤岛
题目链接
题解:DFS
三、小结
一、做题心得
今天做题时间比较晚了,只打卡完成了岛屿问题后续的两道题,剩下两道后边补。
对我个人而言,更习惯用 DFS 解决这一类搜索问题,今天也是用的DFS实现,两道题整体思路和昨天的岛屿问题一致,多的就是需要处理孤岛与边缘陆地的问题。
二、题目与题解
题目一:卡码网 101. 孤岛的总面积
题目链接
101. 孤岛的总面积 (kamacoder.com)
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
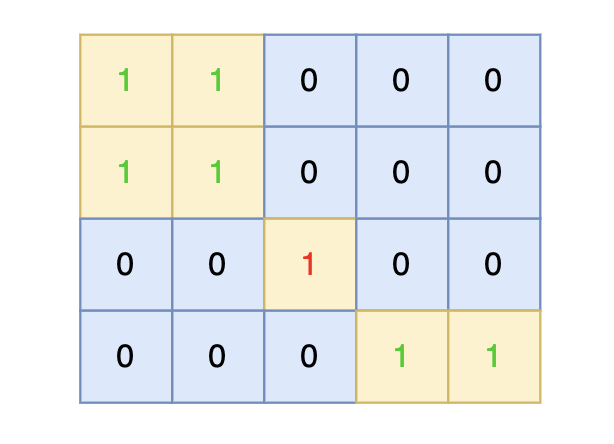
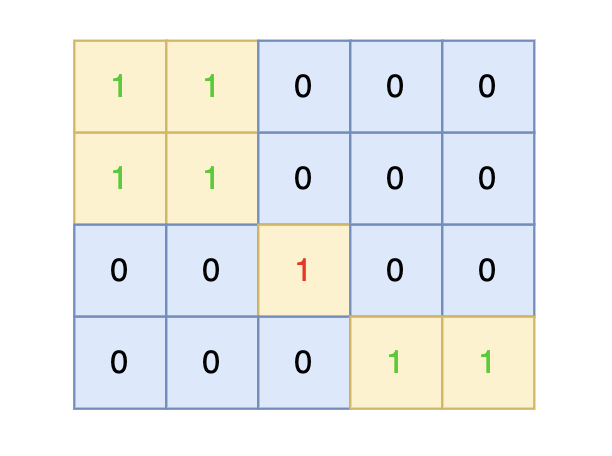
4 5 1 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 1输出示例
1提示信息
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
数据范围:
1 <= M, N <= 50。
题解:DFS
对于处理孤岛总面积的关键:
要求找到孤岛即不靠边的陆地面积,那么我们只要从周边找到陆地然后通过dfs将周边靠陆地且相邻的陆地都变成水 -- 将边缘陆地(边缘岛屿)变成水,然后再去重新遍历地图统计此时还剩下的陆地就可以了。
分别处理四个边缘,我们从边缘向中间靠近,对于同一片边缘岛屿的陆地,都变成水,剩下的陆地就是孤岛,求出其面积即可。即:
// 左右边缘
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) {
dfs(i, 0); // 如果左边缘有陆地,则清除
}
if (grid[i][m - 1] == 1) {
dfs(i, m - 1); // 如果右边缘有陆地,则清除
}
}
// 上下边缘
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) {
dfs(0, j); // 如果上边缘有陆地,则清除
}
if (grid[n - 1][j] == 1) {
dfs(n - 1, j); // 如果下边缘有陆地,则清除
}
}其中,陆地变为水: grid[curx][cury] = 0;
完整代码如下(主体代码就和昨天打卡一致,这里就不细说了):
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int n, m;
int grid[N][N];
bool visited[N][N] = {0};
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int ans = 0;
void dfs(int curx, int cury) {
grid[curx][cury] = 0; // 将当前边缘陆地变成水
ans++; // 计算当前岛屿的大小
for (int i = 0; i < 4; i++) {
int nextx = curx + dx[i], nexty = cury + dy[i];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) {
continue;
}
if (visited[nextx][nexty] || grid[nextx][nexty] == 0) {
continue;
}
visited[nextx][nexty] = true;
dfs(nextx, nexty);
}
}
int main() {
std::ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
/* 遍历网格的边缘,并使用dfs清除所有靠边的陆地 */
// 左右边缘
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) {
dfs(i, 0); // 如果左边缘有陆地,则变为是水
}
if (grid[i][m - 1] == 1) {
dfs(i, m - 1); // 如果右边缘有陆地,则变为水
}
}
// 上下边缘
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) {
dfs(0, j); // 如果上边缘有陆地,则变为水
}
if (grid[n - 1][j] == 1) {
dfs(n - 1, j); // 如果下边缘有陆地,则变为水
}
}
// 重置结果,开始计算不靠边的陆地面积
ans = 0;
for (int i = 0; i < n; i++) { // 再次遍历网格
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) { // 如果是陆地且不靠边
dfs(i, j); // 使用dfs计算陆地的大小
}
}
}
cout << ans << endl; // 输出边缘陆地即不靠边的陆地总面积
return 0;
}题目二:卡码网 102. 沉没孤岛
题目链接
102. 沉没孤岛 (kamacoder.com)
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。 注意:每个元素后面都有一个空格
输入示例
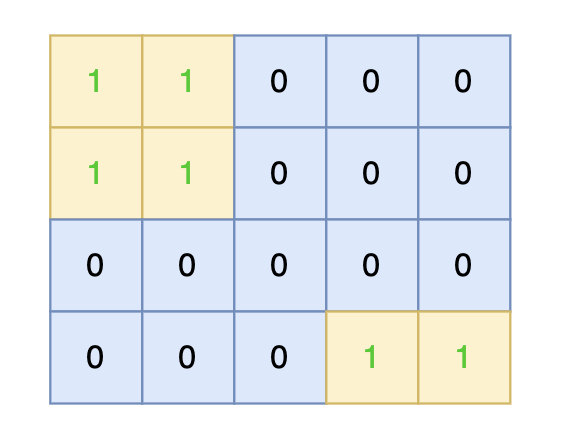
4 5 1 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 1输出示例
1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1提示信息
将孤岛沉没。
数据范围:
1 <= M, N <= 50。
题解:DFS
这题和上题思路基本一致,这里有个很巧妙的解法:将边缘岛屿的陆地全标记为 2,孤岛不做标记(仍为1),最后将原本的 1 (孤岛)变为 0,边缘陆地的 2 变为 1 ,就实现了孤岛的沉没。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int n, m;
int grid[N][N];
bool visited[N][N] = {0};
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void dfs(int curx, int cury) {
grid[curx][cury] = 2; // 注意:将边缘孤岛(边缘陆地)标记为 2
for (int i = 0; i < 4; i++) {
int nextx = curx + dx[i], nexty = cury + dy[i];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) {
continue;
}
if (visited[nextx][nexty] || grid[nextx][nexty] == 0) {
continue;
}
visited[nextx][nexty] = true;
dfs(nextx, nexty);
}
}
int main() {
std::ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
/* 遍历网格的边缘,并使用dfs清除所有靠边的陆地 */
// 左右边缘
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) {
dfs(i, 0); // 如果左边缘有陆地,则记为2
}
if (grid[i][m - 1] == 1) {
dfs(i, m - 1); // 如果右边缘有陆地,记为2
}
}
// 上下边缘
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) {
dfs(0, j); // 如果上边缘有陆地,则记为2
}
if (grid[n - 1][j] == 1) {
dfs(n - 1, j); // 如果下边缘有陆地,则记为2
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) { //沉没孤岛 -- 孤岛从 1 变为 0
grid[i][j] = 0;
}
if (grid[i][j] == 2) { // 边缘岛屿的陆地保留 -- 2 回到 1
grid[i][j] = 1;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m - 1; j++) {
cout << grid[i][j] << " ";
}
cout << grid[i][m - 1] << endl;
}
return 0;
}三、小结
图论这一块内容相对来说难度较大,但其实理清思路了慢慢去写也能够收获很多。今天的打卡先到此结束,后边会继续加油!