Hello , 大家好 , 这个专栏给大家带来的是 Redis 系列 ! 本篇文章给大家讲解的是 Redis 中 Zset 类型的相关内容 , 它在 set 类型的基础上又引入了 score 属性 , 那我们可以一起来看看 score 具体起到了什么作用 .

本专栏旨在为初学者提供一个全面的 Redis 学习路径，从基础概念到实际应用，帮助读者快速掌握 Redis 的使用和管理技巧。通过本专栏的学习，能够构建坚实的 Redis 知识基础，并能够在实际学习以及工作中灵活运用 Redis 解决问题 .
专栏地址 : Redis 入门实践

---

一 . zset 的引入

我们之前学习过 set 类型 . 他有两个显著的特点

1. 唯一 : set 中的元素不能重复
2. 无序 : set 中的元素是无序的 , 比如 : [1 , 2 , 3] 和 [3 , 2 , 1] 是同一个集合

而 list 是要求有序的 , [1 , 2 , 3] 和 [3 , 2 , 1] 不是同一个列表
那大家要注意一点 : 我们的有序集合 (Zset) 中的有序和列表 (list) 中的有序不是一个有序 .

• Zset 中的有序指的是升序 / 降序
• list 中的有序指的是顺序固定

那 Zset 既然是有序的 , 那它所排序的规则是什么 ?
为了方便描述排序规则 , 我们给 Zset 的 member 中同时引入了一个属性 : score (分数) , 他是浮点类型的 . 每个 member 都会分配一个分数 . 进行排序就按照此处的分数大小来进行升序 / 降序排序 .

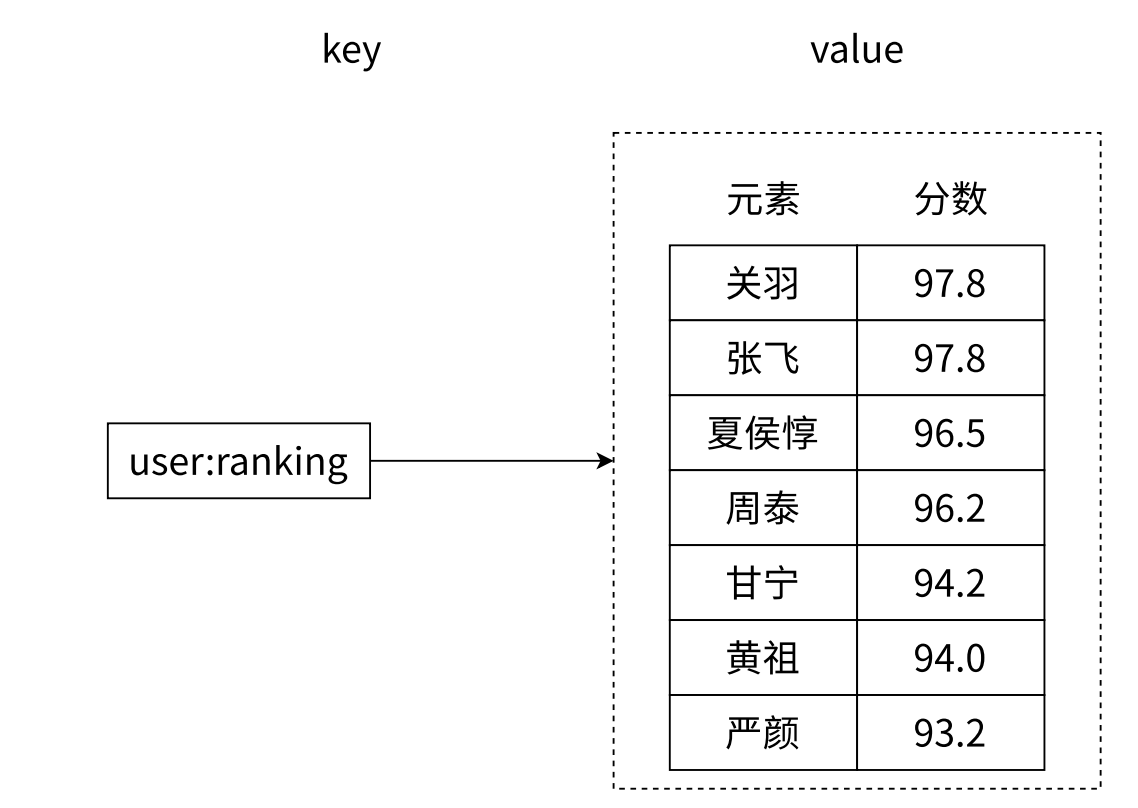
我们从图片里面也可以看到 , 在 value 中给每个元素都分配了一个分数属性 .

那 Zset 也是 set , 也要求元素是不能重复的 , 但是分数是可以重复的 .

Zset 主要还是用来存储元素的 , 分数属性只是起到了一个辅助的作用

那我们再来对比一下 list、set、Zset 的具体区别

数据结构	是否允许重复元素	是否有序	有序依据	应用场景
列表	是	是	索引下标	消息队列等
集合	否	否		用户标签等
有序集合	否	是	分数属性	排行榜系统等

二 . 常见命令

2.1 zadd、zrange

zadd 的作用是向有序集合中添加元素以及分数属性
语法 : zadd key score1 member1 [score2 member2]

在添加的时候 , 既需要添加元素 , 又需要添加分数属性

如果当前的 member 并不存在 , 此时就会达到添加新 member 的效果 . 如果 member 已经存在 , 此时就会更新分数
时间复杂度 : O(logN) , N 指的是有序集合中的元素个数

由于 Zset 是有序结构 , 要求新增的元素就必须要放到合适的位置上

返回值代表新增成功元素的个数

如果产生了修改操作 , 那返回值是返回 0 而不是 1 , 因为修改操作并不算新增元素

如果多个元素有相同的分数 , 那么相同的元素之间就按照字典序进行排列

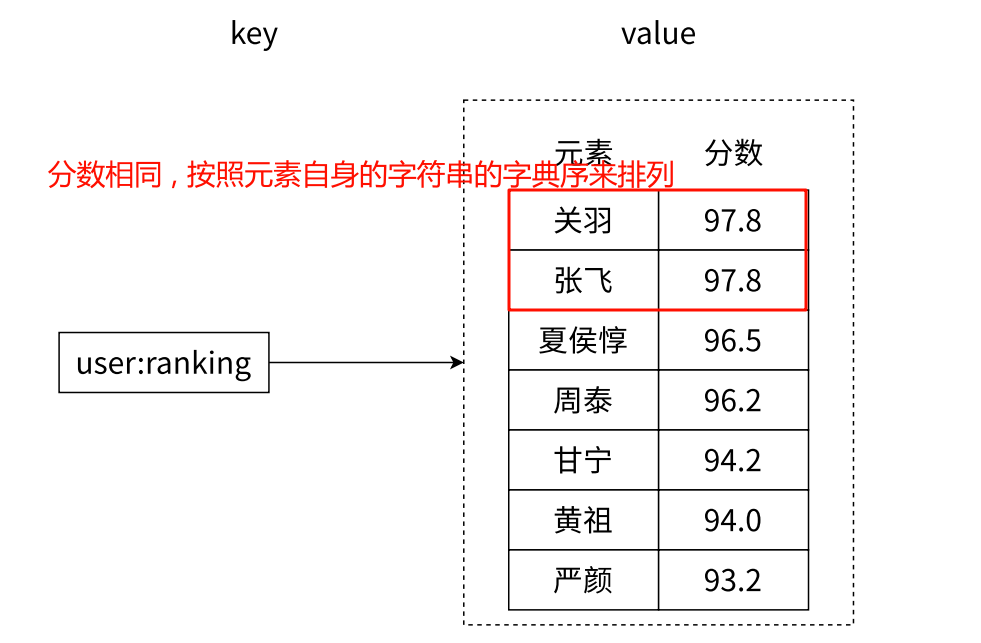
如果多个元素分数不同 , 那么这些元素之间依然以 score 来进行升序排列 .

Zset 的默认排序方式是升序的 .

那 zadd 还有一系列的额外属性可以设置
zadd key [nx | xx] [gt | lt] [ch] [incr] score1 member1 [score2 member2]
我们分别来看 :

1. [nx | xx] : nx 表示不存在才去设置 , 而 xx 指的是存在才去设置 (相当于更新操作)

我们的 nx / xx 实际上并不是针对 key 来去判断的 , 而是根据 member 来去判断的 .
如果 member 不存在 , nx 就会设置成功 , 但是如果 member 存在 , nx就会设置失败 .
如果 member 存在 , xx 就会设置成功 , 但是如果 member 不存在 , xx 就会设置失败 .

2. [gt | lt] : 如果要插入的元素不存在 , 正常插入 ; 如果要插入的元素存在 , 那就需要判断下面两条规则
   1. gt (greater than) : 大于 , 如果新的分数 > 当前分数 , 更新才会成功
   2. lt (less than) : 小于 , 如果新的分数 < 当前分数 , 更新才会成功

也就是说我们现在要更新分数属性了 , lt 的规则是如果给定的新的分数比之前的分数小 , 就会更新成功 . gt 的规则是如果给定的新的分数比之前的分数大 , 就会更新成功

3. [ch] : 描述了返回值要返回什么信息 . 本来 zadd 的返回值为新增成功的元素个数 , 如果我们添加了 ch , 也会返回集合中被修改的元素个数
4. [incr] : 对集合中的分数属性进行运算 , 比如 : 加减分数等等

如果我们想要查看有序集合中的元素 , 使用 zrange 这个命令即可
语法 : zrange key start stop [withscores]

zrange key 0 -1 就是查看有序列表中所有的元素
[withscores] 的作用是也打印出元素对应的分数属性

时间复杂度 : O(log(N) + M)

O(log(N)) 是根据下标找到边界值
O(M) 是需要遍历每个元素他的成绩属性 , 也就是 stop~end 之间的元素个数

接下来我们通过一些具体操作来理解 zadd 和 zrange 这两个命令
先来看一下 zadd 的基本操作

127.0.0.1:6379> zadd key 99 甄嬛 88 沈眉庄 77 安陵容 # 向有序集合中添加元素
(integer) 3
127.0.0.1:6379> zrange key 0 -1 # 获取有序集合中所有的元素
1) "\xe5\xae\x89\xe9\x99\xb5\xe5\xae\xb9"
2) "\xe6\xb2\x88\xe7\x9c\x89\xe5\xba\x84"
3) "\xe7\x94\x84\xe5\xac\x9b"

那为什么产生乱码了呢 ?
这是因为 Redis 中存储数据是按照二进制的方式来去存储的 , 它并不负责字符的编码与解码的 , 也就是说存进去 Redis 的数据是什么 , 那取出来就是他的二进制结果
如果我们想打印中文 , 我们就需要交给 Redis 的客户端来去操作 , 退出 Redis 客户端 (Ctrl C) , 然后通过 redis-cli --raw 来去启动客户端

root@hecs-327683:~# redis-cli --raw # 利用 Redis 的客户端来去打印中文
127.0.0.1:6379> zrange key 0 -1 # 获取有序集合中的元素
安陵容
沈眉庄
甄嬛
127.0.0.1:6379> zrange key 0 -1 withscores # 打印元素以及他的成绩属性
# 默认是升序存放
安陵容
77
沈眉庄
88
甄嬛
99

那我们再模拟一下修改成绩的情况呢 ?
我们刚才也介绍了 , zadd 实际上就是如果没有 member 那就新增 , 如果 member 存在 , 那就是覆盖操作

127.0.0.1:6379> zadd key 90 安陵容 # 修改安陵容的成绩属性
0 # 0 表示没有添加新的元素
127.0.0.1:6379> zrange key 0 -1 withscores 
沈眉庄
88
# 此时修改安陵容的成绩属性 , 就导致了之前的顺序改变了
# 那 Redis 就会自动的移动元素的位置 , 保证升序排列
安陵容
90
甄嬛
99

接下来 , 我们来去模拟 zadd 的各种属性的操作
(1) nx : 只能添加新元素 , 不会影响已经存在的元素
(2) xx : 只能更新已有的元素 , 不会添加新元素

127.0.0.1:6379> zadd key nx 93 皇后 # 利用 nx 添加一条不存在的元素
1 # 返回值为 1 代表新增成功一条元素
127.0.0.1:6379> zrange key 0 -1 withscores
沈眉庄
88
安陵容
90
# 新增的元素也按照正确的顺序插入进来了
皇后
93
甄嬛
99
127.0.0.1:6379> zadd key nx 50 皇后 # nx 对已经存在的元素不会产生任何影响
0 # 返回值为 0 代表没有新增元素
127.0.0.1:6379> zrange key 0 -1 withscores
沈眉庄
88
安陵容
# 皇后的成绩修改失败 -> nx 只能插入不存在的数据
90
皇后
93
甄嬛
99
------
127.0.0.1:6379> zadd key xx 50 皇后 # 利用 xx 来去修改皇后的成绩
0 # 返回值为 0 代表没有添加元素
127.0.0.1:6379> zrange key 0 -1 withscores
# 此时皇后的成绩修改成功
皇后
50
沈眉庄
88
安陵容
90
甄嬛
99
127.0.0.1:6379> zadd key xx 88 端妃 # xx 不能插入新的数据
0 # 返回值为 0 代表没有添加元素
127.0.0.1:6379> zrange key 0 -1 withscores
# 此时端妃没插入进来 -> xx 只能进行更新操作
皇后
50
沈眉庄
88
安陵容
90
甄嬛
99

(3) 默认情况下 zadd 命令返回的是添加成功的元素个数 , 但是我们如果指定 ch 这个选项之后 , 返回值就还会包含本次更新的元素的个数

127.0.0.1:6379> zadd key ch 80 皇后 # 修改皇后的成绩 , 添加 ch 选项表示返回值也包括了更新元素的个数
1 # 成功更新一条数据
127.0.0.1:6379> zrange key 0 -1 withscores
# 此时皇后的数据也更新成功了
皇后
80
沈眉庄
88
安陵容
90
甄嬛
99

(4) incr 的作用是将元素的分数加上指定的分数 (就相当于更新操作) , 但是如果使用 incr , 那此时只能指定一个元素和一个分数

127.0.0.1:6379> zadd key incr 10 皇后 # 对皇后的成绩进行 +10
90 # 返回值代表添加之后的成绩
127.0.0.1:6379> zrange key 0 -1 withscores
沈眉庄
88
# 如果成绩相同 , 那就按照元素的字典序进行排列
安陵容
90
# 此时皇后的成绩添加成功
皇后
90
甄嬛
99

2.2 zcard

zcard 的作用是用来获取有序集合中的元素个数
语法 : zcard key
时间复杂度 : O(1)

127.0.0.1:6379> zrange key 0 -1 withscores
# 一共有四个元素
沈眉庄
88
安陵容
90
皇后
90
甄嬛
99
127.0.0.1:6379> zcard key # 获取有序集合中的元素个数
4

2.3 zcount

zcount 的作用是按照分数区间来进行筛选 , 也就是说筛选 [min , max] 之间符合的元素个数
语法 : zcount key min max

min 和 max 默认是闭区间 , 如果我们想排除边界值 , 我们就需要在 min 和 max 的左侧加上括号 (比较奇葩 , 大家仔细观察)

时间复杂度 : O(logN)

zcount 需要制定 min 和 max 分数区间的 , 那就需要先根据 min 找到对应的元素 , 再根据 max 找到对应的元素 , 这两个操作都是 logN 的操作 , 那在这两个元素之间所有的元素都是符合条件的元素

127.0.0.1:6379> zrange key 0 -1 withscores
沈眉庄
88
安陵容
90
皇后
90
甄嬛
99
# 反人类 !!!
127.0.0.1:6379> zcount key 90 99 # 查询分数在 [90,99] 之间的元素个数
3
127.0.0.1:6379> zcount key (90 99 # 查询分数在 (90,99] 之间的元素个数
1
127.0.0.1:6379> zcount key 90 (99 # 查询分数在 [90,99) 之间的元素个数
2
127.0.0.1:6379> zcount key (88 (99 # 查询分数在 (90,99) 之间的元素个数
2

那 min 和 max 也是可以写成浮点数的 , 那在浮点数中有存在两个特殊的数值

1. inf : 无穷大
2. -inf : 负无穷大

那在 Zset 中分数也是支持使用 inf 和 -inf 的

127.0.0.1:6379> zcount key -inf inf # 查询分数在 [-∞,+∞] 之间的元素个数
4

2.4 zrevrange、zrangebyscore

zrevrange 是按照成绩降序打印
语法 : zrevrange key start stop [withscores]
时间复杂度 : O(log(N) + M)

127.0.0.1:6379> zrevrange key 0 -1 withscores # 降序打印有序集合中的元素
# 此时元素都按照降序排列了
甄嬛
99
皇后
90
安陵容
90
沈眉庄
88

zrangebyscore 是按照成绩来去查找元素的 , 查找成绩在 [min , max] 区间内的元素
语法 : zrangebyscore key min max [withscores]

127.0.0.1:6379> zrangebyscore key 90 100 withscores # 查询成绩在 [90,100] 之间的元素
安陵容
90
皇后
90
甄嬛
99

但是这个命令比较遗憾 , 在 6.2.0 之后会被废弃 , 会被合并到 zrange 中去使用

2.5 zpopmax、zpopmin

zpopmax 的作用是删除并返回成绩最高的 count 个元素
语法 : zpopmax key [count]

其实可以理解为删除堆顶元素 , 也就是 pop() 方法

返回值就是被删除的元素 (member + score)
时间复杂度 : O(log(N) * M)

N 是有序集合的元素个数 , O(log(N)) 指的是我们需要先查找成绩最高的元素
M 是要删除的元素个数 , 意思就是删除几个元素就查找几次成绩最高的元素

127.0.0.1:6379> zpopmax key # 弹出成绩最高的元素
甄嬛
99
127.0.0.1:6379> zpopmax key 2 # 弹出两个成绩最高的元素
皇后
90
安陵容
90

如果存在多个元素 , 他们的分数相同并且同时为最大值 , 那 zpopmax 删除元素的时候 , 该怎么删除呢 ?
分数虽然是主要因素 , 但是如果分数相同就会按照 member 的字典序来决定弹出的先后顺序

127.0.0.1:6379> zadd key 99 甄嬛 99 皇后 88 沈眉庄 # 构造两组成绩相同的数据
2
127.0.0.1:6379> zrange key 0 -1 withscores
沈眉庄
88
# 甄嬛和皇后的成绩相同
甄嬛
99
皇后
99
127.0.0.1:6379> zpopmax key # 删除成绩最高的元素
# 删除的是皇后 , 这是因为皇后的字典序比甄嬛高
皇后
99

zpopmin 是删除并返回成绩最小的元素
语法 : zpopmin key [count]
时间复杂度 : O(log(N) * M)

N 是有序集合的元素个数 , O(log(N)) 指的是我们需要先查找成绩最高的元素
M 是要删除的元素个数 , 意思就是删除几个元素就查找几次成绩最高的元素

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu # 向有序集合中添加元素
(integer) 3
127.0.0.1:6379> zrange key 0 -1 withscores # 查看有序集合中所有元素(默认升序排列)
1) "zhangsan"
2) "10"
3) "lisi"
4) "20"
5) "wangwu"
6) "30"
127.0.0.1:6379> zpopmin key # 删除并返回成绩最低的元素
1) "zhangsan"
2) "10"
127.0.0.1:6379> zpopmin key 2 # 删除并返回两个成绩最低的元素
1) "lisi"
2) "20"
3) "wangwu"
4) "30"

2.6 bzpopmax、bzpopmin

bzpopmax 就是阻塞版本的 zpopmax , 如果有序集合中已经有了元素 , 那就直接返回 ; 如果没有元素 , 就会产生阻塞
我们的有序集合也可以视为是一个优先级队列 , 那我们就可以实现一个带有阻塞功能的优先级队列
语法 : bzpopmax key1 [key2 …] timeout
其中 , 每个 key 都是一个有序集合 , timeout 表示超时时间 (最多阻塞多久) , 单位为 s .

timeout 可以设置小数形式 , 比如 : 0.1s 就是 100ms

它的特性也是在有序集合为空的时候开始阻塞 , 等到其他客户端插入数据就解除阻塞
时间复杂度 : O(logN)

O(logN) 需要先找到成绩最高的元素 , 然后删除

如果 bzpopmax 同时监听了多个 key , 那么他的时间复杂度依然是 O(logN) , 因为我们 bzpopmax 是删除成绩最高的元素 , 我们只需要删除这一个元素即可 , 不用乘 M

我们可以看一下演示

那他执行的流程就是这个样子的

其中 , 返回值包含了三部分信息

1) "key" # 表示是哪个有序集合添加了元素
# 成绩最高的元素
2) "wangwu"
3) "70"
(4.52s)

同理 , bzpopmin 的用法与 bzpopmax 用法相同

2.7 zrank、zrevrank

zrank 的作用是返回指定元素的排名

所谓的排名 , 实际上就是下标

语法 : zrank key member
时间复杂度 : O(logN)

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu # 向有序集合中添加元素
(integer) 3
127.0.0.1:6379> zrank key lisi # 返回 lisi 所在的下标
(integer) 1
127.0.0.1:6379> zrank key wangwu # 返回 wangwu 所在的下标
(integer) 2
127.0.0.1:6379> zrank key zhangsan # 返回 zhangsan 所在的下标
(integer) 0
127.0.0.1:6379> zrank key error # 元素不存在会返回 nil
(nil)

zrevrank 也是获取到 member 的下标 , 但是他是按照降序的顺序来获取下标 (也就是反着运算下标)

127.0.0.1:6379> zrevrank key zhangsan # 降序获取 zhangsan 的下标
(integer) 2
127.0.0.1:6379> zrevrank key wangwu # 降序获取 wangwu 的下标
(integer) 0

2.8 zscore

zscore 的作用是查询指定 member 的分数
时间复杂度 : O(1)

Redis 对 zscore 的查询做了特殊的优化 , 并不再是 O(logN) 了

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu # 向有序集合中添加元素
(integer) 3
127.0.0.1:6379> zscore key zhangsan # 查询元素 zhangsan 的分数
"10"
127.0.0.1:6379> zscore key lisi # 查询元素 lisi 的分数
"20" 
127.0.0.1:6379> zscore key wangwu # 查询元素 wangwu 的分数
"30"

2.9 zrem、zremrangebyrank、zremrangebyscore

zrem 的作用是删除有序集合中指定的元素
语法 : zrem key member1 [member2 …]
时间复杂度 : O(log(N) * M)

N 指的是有序集合中的元素个数 , M 指的是要删除的元素个数
删除一个元素需要 O(logN) , 总共需要删除 M 个元素

127.0.0.1:6379> zrem key zhangsan # 删除元素 zhangsan
(integer) 1 # 返回值代表删除成功的元素个数
127.0.0.1:6379> zrem key lisi wangwu # 删除多个元素 lisi wangwu
(integer) 2

那 zremrangebyrank 的作用是按照排序结果升序删除指定下标范围的元素 , 也就是删除 [start , stop] 区间段的元素
语法 : zremrangebyrank key start stop
时间复杂度 : O(log(N) + M)

N 指的是有序集合的元素个数 , M 是 start~end 区间中的元素个数
思路就是我们先找到 start 位置的元素 , 时间复杂度为 O(logN) , 然后只需要往后再找 M 个元素即可 , 也就是 O(log(N) + M)

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu 40 zhaoliu # 向有序集合中添加元素
(integer) 4
127.0.0.1:6379> zremrangebyrank key 1 2 # 删除下标在 [1,2] 之间的元素
(integer) 2
127.0.0.1:6379> zrange key 0 -1 withscores
# 下标为 1 的 lisi 和下标为 2 的 wangwu 就被删除掉了
1) "zhangsan"
2) "10"
3) "zhaoliu"
4) "40"

zremrangebyscore 是按照成绩来去删除元素 , 在 [min , max] 区间的成绩所对应的元素就会被删除
语法 : zremrangebyscore key min max

同样可以使用 ( 来去排除边界值的

时间复杂度 : O(log(N) * M)

N 指的是有序集合中的元素个数 , M 指的是要删除的区间内的元素个数
删除一个元素需要 O(logN) , 总共需要删除 M 个元素

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu 40 zhaoliu # 向有序集合中添加元素
(integer) 4
127.0.0.1:6379> zremrangebyscore key 20 30 # 删除成绩在 [20,30] 区间范围的元素
(integer) 2
127.0.0.1:6379> zrange key 0 -1
# 成绩为 20 的 lisi 和成绩为 30 的 wangwu 就被删除了
1) "zhangsan"
2) "zhaoliu"

2.10 zincrby

zincrby 为指定的元素的分数进行修改
语法 : zincrby key increment member

127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu 40 zhaoliu # 向有序集合中添加元素
(integer) 4
127.0.0.1:6379> zincrby key 15 zhangsan # 对 zhangsan 的成绩 + 15 分
"25"
127.0.0.1:6379> zrange key 0 -1 withscores
1) "lisi"
2) "20"
# 此时有序集合的顺序也随之改变了
3) "zhangsan"
4) "25"
5) "wangwu"
6) "30"
7) "zhaoliu"
8) "40"
127.0.0.1:6379> zincrby key -15 zhangsan # 对 zhangsan 的成绩 - 15 分
"10"
127.0.0.1:6379> zrange key 0 -1 withscores
# 此时有序集合的顺序也随之改变了
1) "zhangsan"
2) "10"
3) "lisi"
4) "20"
5) "wangwu"
6) "30"
7) "zhaoliu"
8) "40"
127.0.0.1:6379> zincrby key 0.5 zhangsan # zincrby 也可以加减小数
"10.5"
127.0.0.1:6379> zrange key 0 -1 withscores
# zhangsan 的成绩已经 + 0.5 了
1) "zhangsan"
2) "10.5"
3) "lisi"
4) "20"
5) "wangwu"
6) "30"
7) "zhaoliu"
8) "40"

2.11 集合间操作

我们之前学习过 set 类型 , 他也存在集合间操作 , 分别为 : sinter、sunion、sdiff
那相对应的命令就是 zinter、zunion、zdiff ?
并不是 , 这三个命令在 Redis 6.2 之后才引进 , 我们使用的是 Redis 5 系列 , 先不去了解这几个命令
在 Zset 中提供了两个集合间操作

1. zinterstore : 求交集 , 结果保存到另外一个集合中
2. zunionstore : 求并集 , 结果保存到另外一个集合中

交集 : zinterstore

基本语法 : zinterstore destination numkeys key1 [key2 …]

• destination 表示要把结果存储到 destination 中
• numkeys 描述了后续有几个 key 参与交集运算 .

那为什么这里还需要单独描述出几个 key 参与运算呢 ?
主要是因为真正的语法中 , 后续还有很多选项 . 我们指定出 numkeys 描述出 key 的个数之后 , 就可以明确的知道后面的选项是从哪里开始的了
(我们可以类比 HTTP 的协议报文理解 , 通过 Content-Length 来描述正文的长度 , 如果 Content-Length 错误就容易产生粘包问题)

真正的语法 : zinterstore destination numkeys key1 [key2 …] [weights weight1 [weight2 …]] [aggregate <sum | min | max>]

1. [weights weight1 [weight2 …]] : 指的是权重 (优先级) , 我们的有序集合是带有分数的 , 那每个集合他们的权重也是不同的 , 我们求交集既需要考虑相同的元素 , 又需要考虑对应集合的权重 . 权重和元素都相同才算是交集
2. [aggregate <sum | min | max>] :

比如 :
key1 :

zhangsan	10
lisi	20
wangwu	30

key2 :

zhangsan	15
lisi	25
zhaoliu	30

在有序集合中 , member 才是主体 , score 只是用来辅助排序的 , 因此在进行比较相同的时候 , 只要 member 相同即可 , 不要求 score 相同
所以最终的交集就是 : zhangsan、lisi
如果 member 相同 , score 不同 , 那最后的 score 怎么算 ?
这就需要我们的 [aggregate <sum | min | max>] 来运算了 , 以 zhangsan 为例

• sum : 求和 , 最终的 score 为 10 + 15 = 25
• min : 取最小值 , 最终的 score 为 min(10,25) = 10
• max : 求最大值 , 最终的 score 为 max(10,25) = 25

那我们通过命令来去理解一下
先来看最基础的版本

# 此时 , zhangsan 和 lisi 为交集结果
# 元素相同即可 , 不要求成绩相同
127.0.0.1:6379> zadd key1 10 zhangsan 20 lisi 30 wangwu
(integer) 3
127.0.0.1:6379> zadd key2 15 zhangsan 25 lisi 35 zhaoliu
(integer) 3
127.0.0.1:6379> zinterstore key3 2 key1 key2 # 获取 key1 和 key2 中的交集结果保存到 key3 中
(integer) 2 # 返回值代表交集元素的个数
127.0.0.1:6379> zrange key3 0 -1 withscores
1) "zhangsan"
2) "25" # 默认的就是将交集的 score 相加
3) "lisi"
4) "45"

然后我们模拟一下权重的效果

# 此时 , zhangsan 和 lisi 为交集结果
# 元素相同即可 , 不要求成绩相同
127.0.0.1:6379> zadd key1 10 zhangsan 20 lisi 30 wangwu
(integer) 3
127.0.0.1:6379> zadd key2 15 zhangsan 25 lisi 35 zhaoliu
(integer) 3

# 将 key1 的权重设置为 2 , 将 key2 的权重设置为 3
# 也就是 key1 中每个成绩 *2 , key2 中的每个成绩 *3
127.0.0.1:6379> zinterstore key4 2 key1 key2 weights 2 3 
(integer) 2
127.0.0.1:6379> zrange key4 0 -1 withscores
1) "zhangsan"
2) "65" # 10*2+15*3=65
3) "lisi"
4) "115" # 20*2+25*3=115

我们再指定一下 score 的计算方式

# 此时 , zhangsan 和 lisi 为交集结果
# 元素相同即可 , 不要求成绩相同
127.0.0.1:6379> zadd key1 10 zhangsan 20 lisi 30 wangwu
(integer) 3
127.0.0.1:6379> zadd key2 15 zhangsan 25 lisi 35 zhaoliu
(integer) 3

# 将 key1 和 key2 的交集保存到 key5 中
# score 的计算方式为 max(key1.score,key2.score)
127.0.0.1:6379> zinterstore key5 2 key1 key2 aggregate max
(integer) 2
127.0.0.1:6379> zrange key5 0 -1 withscores
1) "zhangsan"
2) "15" # key2 中的 score 更高
3) "lisi"
4) "25" # key2 中的 score 更高
# 将 key1 和 key2 的交集保存到 key6 中
# score 的计算方式为 min(key1.score,key2.score)
127.0.0.1:6379> zinterstore key6 2 key1 key2 aggregate min
(integer) 2
127.0.0.1:6379> zrange key6 0 -1 withscores
1) "zhangsan"
2) "10" # key1 中的 score 更低
3) "lisi" 
4) "20" # key1 中的 score 更低

zinterstore 的时间复杂度为 O(N * K) + O(M * log(M))
我们来看一下官方文档对于时间复杂度的解释 : https://redis.io/commands/zinterstore

时间复杂度我们不需要刻意记忆 , 我们只需要通过时间复杂度来去更好的理解命令即可

并集 : zunionstore

语法 : zunionstore destination numkeys key1 [key2 …] [weights weight1 [weight2 …]] [aggregate <sum | min | max>]
里面的用法和选项跟 zinterstore 类似 , 我们直接通过命令来了解它的用法

# 并集是 zhangsan、lisi、wangwu、zhaoliu
127.0.0.1:6379> zadd key1 10 zhangsan 20 lisi 30 wangwu
(integer) 3
127.0.0.1:6379> zadd key2 15 zhangsan 25 lisi 35 zhaoliu
(integer) 3
127.0.0.1:6379> zunionstore key3 2 key1 key2
(integer) 4 # 返回值表示交集元素的个数
127.0.0.1:6379> zrange key3 0 -1 withscores
# 顺序按照成绩重新进行升序排列
1) "zhangsan"
2) "25" # 默认是 sum(key1.score,key2.score)
3) "wangwu"
4) "30"
5) "zhaoliu"
6) "35"
7) "lisi"
8) "45"
# 将 key1 的权重设置成 0.5 , 将 key2 的权重设置成 0.6
# 也就是 key1 中的每个元素 *0.5 , key2 中的每个元素 *0.6
127.0.0.1:6379> zunionstore key4 2 key1 key2 weights 0.5 0.6
(integer) 4
127.0.0.1:6379> zrange key4 0 -1 withscores
1) "zhangsan"
2) "14" # 10*0.5+15*0.6=14
3) "wangwu"
4) "15" # 30*0.5=15
5) "zhaoliu"
6) "21" # 35*0.6=21
7) "lisi"
8) "25" # 20*0.5+25*0.6=25
# 将 key1 和 key2 的并集保存到 key5 中
# score 的计算方式为 min(key1.score,key2.score)
127.0.0.1:6379> zunionstore key5 2 key1 key2 aggregate min
(integer) 4
127.0.0.1:6379> zrange key5 0 -1 withscores
1) "zhangsan"
2) "10" # min(10,15)=10
3) "lisi"
4) "20" # min(20,25)=20
5) "wangwu"
6) "30" #min(30)=30
7) "zhaoliu"
8) "35" #min(35)=35
# 将 key1 和 key2 的并集保存到 key6 中
# score 的计算方式为 max(key1.score,key2.score)
127.0.0.1:6379> zunionstore key6 2 key1 key2 aggregate max
(integer) 4
127.0.0.1:6379> zrange key6 0 -1 withscores
1) "zhangsan"
2) "15" # max(10,15)=15
3) "lisi"
4) "25" # max(20,25)=25
5) "wangwu"
6) "30" # max(30)=30
7) "zhaoliu"
8) "35" # max(35)=35

小结

三 . 内部编码

有序集合内部的编码方式有两种 :

1. 如果有序集合中的元素个数较少 , 或者单个元素体积不大 , 就会使用 ziplist 来去存储
2. 如果有序集合中的元素个数较多 , 或者单个元素体积非常大 , 就会使用 skiplist (跳表) 来去存储

跳表就类似一个二叉搜索树 , 他查询元素的时间复杂度是 O(logN) . 但是跳表更适合按照范围来去获取元素

# 有序集合中的元素个数较少 && 单个元素体积不大 -> ziplist
127.0.0.1:6379> zadd key 10 zhangsan 20 lisi 30 wangwu 
(integer) 3
127.0.0.1:6379> object encoding key
"ziplist"
# 有序集合中的元素个数较大 || 单个元素体积比较大 -> skiplist
127.0.0.1:6379> zadd key 40 aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
(integer) 1
127.0.0.1:6379> object encoding key
"skiplist"

具体的跳表的相关细节 , 我们之后专门来去给大家介绍

四 . 应用场景 : 排行榜

关于排行榜 , 也有很多具体的说法 , 比如 : 微博热搜、游戏天梯排行、成绩排行 …
排行榜非常重要的要素就是用来排行的分数是实时变化的 , 那使用 Zset 来完成排行榜是非常简单的 .
比如游戏天梯排行 , 我们只需要把玩家信息和对应分数放到有序集合中即可 , 自动就形成了排行榜 . 我们随时可以按照排行 (下标) 或者按照分数进行范围查询来去生成排行榜 .
而且随着分数发生变化 , 可以使用 zincrby 来去修改分数 , 并且最终的排行顺序也可以自动调整 (O(logN) 的时间复杂度)

但是有的排行榜也会更复杂一些 , 比如微博热搜这种 , 他不只与浏览量有关 , 还需要考虑点赞量、转发量、评论量等等因素 , 那通过 Zset 实现也很简单 , 可以通过权重分配的方式 , 通过 zinterstore / zunionstore 来去计算热度 .
我们可以将浏览量、点赞量、评论量、转发量所对应的数值分别存放到不同的有序集合中 , member 就是微博的 ID , score 就是各自维度所对应的数值 , 我们通过 zinterstore / zunionstore 就可以把上述有序集合按照约定好的权重去进行集合间运算即可 , 那最后得到的结果集合就是我们所需要的热度 .

---

今天关于 zset 的分享就结束了 , 如果对你有帮助的话 , 还请一键三连~