目录
- 前言
- 一、顺序表
- 1.1 顺序表的定义及其特点
- 1.2 顺序表的C语言实现
- 1.2.1 定义顺序表
- 1.2.2 初始化
- 1.2.3 插入
- 1.2.4 删除
- 1.2.5 查找
- 二、链表
- 2.1 链表的定义
- 2.2 单向链表的实现
- 2.2.1 定义单向链表
- 2.2.2 创建链表
- 2.2.3 插入元素
- 2.2.4 删除元素
- 2.2.5 查找
- 2.3 双向循环链表
前言
线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear list)是数据结构的一种,一个线性表是n个具有相同特性的数据元素的有限序列。线性表又称线性存储结构,是最简单的一种存储结构,线性表存储数据的实现方案有两种,分别是:顺序存储结构和链式存储结构

一、顺序表
1.1 顺序表的定义及其特点
顺序表即线性表的顺序存储结构,最简单的顺序表为数组。它是用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。顺序表存储数据的具体实现方案是:将数据全部存储到一整块内存空间中,数据元素之间按照次序挨个存放。
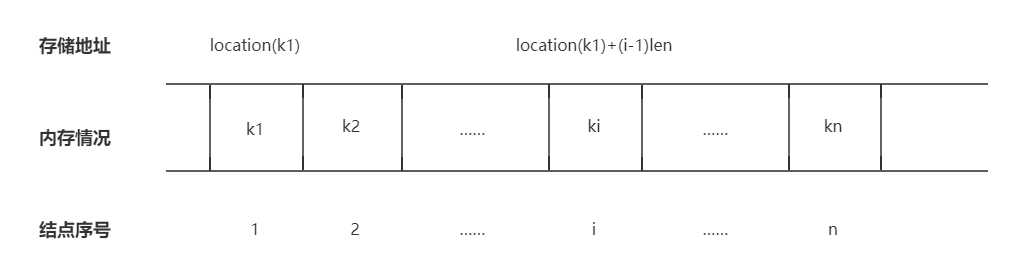
其有如下特点:
- 随机访问:可通过首地址和元素序号在单位时间O (1)内找到指定的元素。
- 存储密度高:存储密度高是因为每个结点存储空间指用来存储数据元素,没有别的额外开销。
- 物理位置相邻:物理位置和逻辑位置一样,保持相邻,因此插入和删除元素需要移动大量元素,比较耗时。
1.2 顺序表的C语言实现
1.2.1 定义顺序表
加入stdbool.h引入bool型变量
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int DataType //定义存储类型
#define Maxsize 50 //线性表最大长度
typedef struct
{
DataType data[Maxsize]; //顺序表的元素
int len; //顺序表当前长度
}SqList; //顺序表的定义类型
1.2.2 初始化
//初始化只要清零长度
void InitList(SqList *L)
{
L->len=0;
}
1.2.3 插入
//定义插入顺序表的函数:在第i个元素之前插入x
//返回值:0-插入失败;1-插入成功
bool ListInsert(SqList *L,int i,int x)
{
int j;
//判断插入后是否溢出
if(L->length >= MaxSize)
{
printf("顺序表已满,无法进行插入操作!");
return 0;
}
//判断插入位置是否合法
else if((i<=0) || (i>L->length+1))
{
printf("插入的位置不正确!");
return 0;
}
for(j=L->len-1;j>=i-1;j--)
{
L->data[j+1]=L->data[j];
}
//在第i个元素之前插入就是把从i开始的元素往后移,然后赋值给第i个元素,在数组中就是i-1了
L->data[i-1]=x;
L->len++; //插入完之后数组长度+1
return 1;
}
1.2.4 删除
//定义删除顺序表元素函数,删除第i个元素
//返回值:0-删除失败;1-删除成功
bool ListDelete(SqList *L,int i)
{
int j;
if((i<1) || (i>L->len))//和插入是一样的判断条件
{
printf("删除位置错误");
return 0;
}
//删除第i个元素就是从第i个元素开始一个一个地从后向前覆盖
for(j=i;j<L->len;j++)
{
L->data[j-1]=L->data[j];
}
L->len--;//数组长度-1
return 1;
}
1.2.5 查找
// 在顺序表中查找第一个值等于x的元素,并返回
int findElem(SqList *L, int x)
{
int i;
for(i=0;i<L->len;i++)
{
if(x==L->data[i])
return i; //找到返回下标
}
return -1; //没找到返回-1
}
二、链表
2.1 链表的定义
链表是一个在物理存储单元中非连续、非顺序的的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,有一系列结点(地址)组成,结点可动态的生成。链表分为三类:单向链表,双向链表,循环链表。

节点包括两个部分:
- 一部分存储数据元素的数据域(存储对象)
- 另一部分是存储下一个节点地址的指针域(引用下一个节点)。
其有以下特点
- 优点:和线性表顺序结构相比,链表结构插入,删除操作不需要移动所有节点,不需要初始化容量。
- 缺点:搜索时必须遍历节点,含有大量引用,占空间大。
2.2 单向链表的实现
2.2.1 定义单向链表
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int DataType;
typedef struct ListNode{
DataType data; //代表数据域
struct ListNode * next; //代表指针域,指向直接后继元素
}SList;
2.2.2 创建链表
//输入:arr[]-数组;n-数组长度
//返回值:链表
SLink* CreateList(int arr[], int n)
{
int i;
SList* head = NULL; // 头节点指针
SList* tail = NULL; // 头节点指针
for (i = 0; i < n; i++)
{
// 创建新节点并为其分配内存
SList* newNode = (SList*)malloc(sizeof(SList));
if (newNode == NULL) {
printf("内存分配失败.");
return NULL;
}
// 设置新节点的数据
newNode->data = arr[i];
newNode->next = NULL;
if (head == NULL)
{
head = tail = newNode;
}
else
{
tail->next = newNode;
tail = tail->next;
}
}
return head;
}
2.2.3 插入元素
void Insert(SList** headRef, int position, int value)
{
int count = 1;
SList* p = *headRef;//创建临时结点
SList* newNode = (SList*)malloc(sizeof(SList));// 创建新节点并为其分配内存
if (newNode == NULL) {
printf("内存分配失败。\n");
return;
}
newNode->data = value;
// 如果要插入的位置是链表的头部或链表为空
if(*headRef == NULL || position == 0) {
newNode->next = *headRef;
*headRef = newNode;
return;
}
// 找到要插入位置的前一个节点
while (p->next != NULL && count < position) {
p = p->next;
count++;
}
// 在指定位置插入节点
newNode->next = p->next;
p->next = newNode;
}
2.2.4 删除元素
void Delete(SList** headRef, int value) {
SList* p = *headRef;
SList* prev = NULL;
// 处理头节点为目标节点的情况
if (p != NULL && p->data == value) {
*headRef = p->next;
free(p);
return;
}
// 遍历链表找到要删除的节点
while (p != NULL && p->data != value) {
prev = p;
p = p->next;
}
// 如果找到了目标节点,则删除它
if (p != NULL) {
prev->next = p->next;
free(p);
}
}
2.2.5 查找
SList* Search(SList* head, int value) {
SLink* p = head;
while (p != NULL) {
if (p->data == value) {
return p; // 返回匹配的节点地址
}
p = p->next;
}
return NULL; // 若没有找到匹配节点,则返回NULL
}
2.3 双向循环链表
双向链表就是除了next后结点还有pre前结点,然后再将尾结点与头节点相连形成循环,就成了双向循环链表,其示意图与定义如下:

typedef int DataType;
typedef struct ListNode
{
struct ListNode *next;
struct ListNode *pre;
DataType data;
}LTNode;