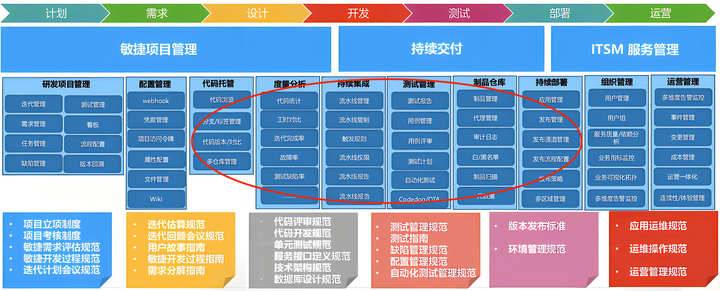
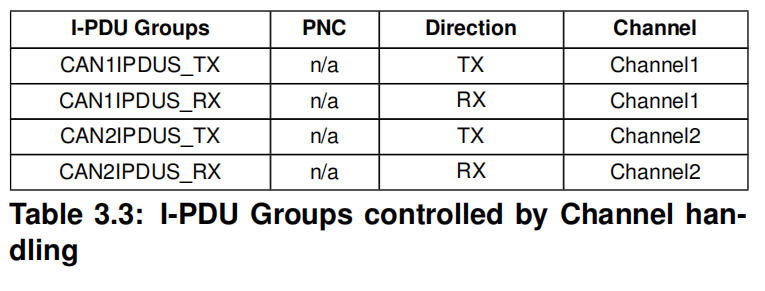
一道模拟题。
思路
最短的路线是直接竖着走下来,经过
n
n
n 个格子,所以
k
k
k 最小是
n
n
n。如果想要延长路线,可以采用九转大肠的形状,就像这样: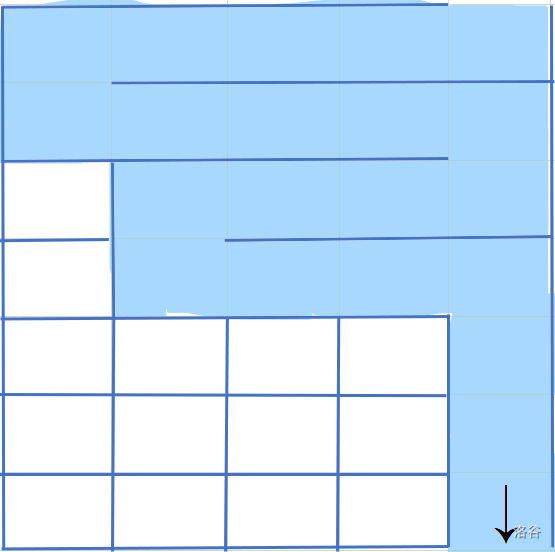
可以发现,每次向左走之后都必须走回来,所以每次新经过的格子数是偶数,得到
k
−
n
k-n
k−n 是偶数才有可行的方案。
首先,把整张图表的初始状态设为如下形式(即每个格点都是独立的):
+++++S+
+o|o|o+
+-+-+-+
+o|o|o+
+++++G+
将
k
k
k 先减去必要的格点数
n
n
n。两行为一组进行考虑,如果此时
k
≥
2
(
m
−
1
)
k\ge2(m-1)
k≥2(m−1) 就意味着可以走到最左边再折回去,于是将两行之间第一列的连接处设为“.”。否则令
t
=
k
/
2
t=k/2
t=k/2,把从右往左第
t
+
1
t+1
t+1 列的两行之间的连接处设为“.”。还有,不要忘记把一行里面左右相邻的格子连接处设为“.”,最后一列通往下一行(下一组的第一行)的连接处也要设为“.”。每次标完之后要将
k
k
k 减去增加的格点数:
m
a
x
(
2
(
m
−
1
)
,
k
)
max(2(m-1),k)
max(2(m−1),k)。
如果行数是奇数并且
k
k
k 不为
0
0
0,那么最后一行需要特殊考虑,可以通过如下图的形式继续延长道路长度:
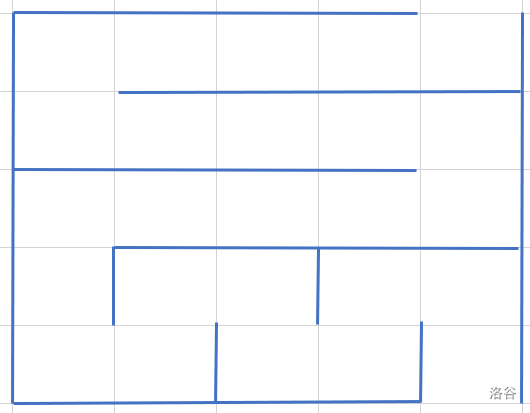
原本的迷宫长这样:

$\$ 此时两列一组考虑,但是最后一列必须空出来,确保通往出口的通道。所以当考虑到一个
2
×
2
2\times2
2×2 的方形(跨越第
n
−
1
n-1
n−1 行和第
n
n
n 行)并且
k
>
0
k>0
k>0 时,要做的事情:
- 在第一行第一列和第一行第二列之间插入一块板子“|”。
- 把其余的连接处都设成“.”。
这样每次可以把道路的长度延长两个格子(
k
k
k 减去
2
2
2),并走回第
n
−
1
n-1
n−1 行。但是如果列数是偶数,最后一列又要走到第
n
n
n 行出迷宫,那么分组时就会多出倒数第二列。所以并不是每个格子都走得到,奇数行偶数列的迷宫里会有一个格子(程序里默认是第
n
n
n 行第
m
−
1
m-1
m−1 列)无法走到(即
k
≤
n
m
−
1
k\le nm-1
k≤nm−1)。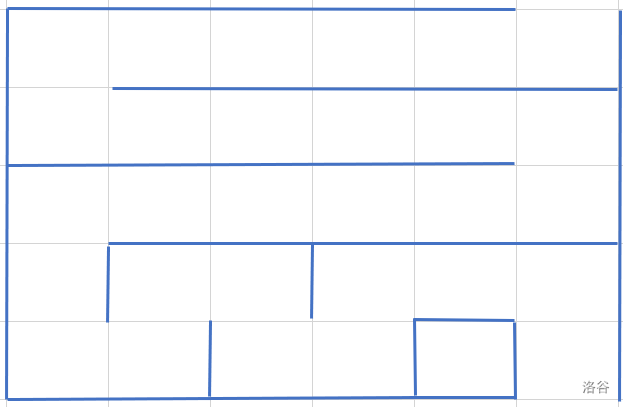
代码实现
就是多画几张图,把输出矩阵中的行号和列号与实际迷宫中的行号和列号对应起来。本人考场上没有考虑最后剩下一行的情况,WA 三个点。
#include<bits/stdc++.h>
using namespace std;
#define maxk (n-1)*m+1
#define mink n
int n,m,k;
char ans[300][300];
void pre(){
for(int i=1;i<=2*m+1;i++){
if(i==2*m) ans[1][i]='S',ans[2*n+1][i]='G';
else ans[1][i]=ans[2*n+1][i]='+';
}
for(int i=1;i<=2*n+1;i++) ans[i][1]=ans[i][2*m+1]='+';
for(int i=2;i<=2*n;i++)
for(int j=2;j<=2*m;j++){
if(i%2==0){
if(j%2==0) ans[i][j]='o';
else ans[i][j]='|';
}
else{
if(j%2==0) ans[i][j]='-';
else ans[i][j]='+';
}
}
}
int main(){
cin>>n>>m>>k;
if(k<mink||(k-n)%2){
cout<<"No"<<endl;
return 0;
}
pre();
k-=n;
for(int i=1;i<=n;i+=2){
if(i==n) break;
if(k>=2*(m-1)){
for(int j=3;j<=2*m-1;j+=2){
ans[2*i][j]='.';
ans[2*i+2][j]='.';
}
k-=2*(m-1);
ans[2*i+1][2]='.';
}
else{
for(int j=2*m-1;j>=2*m-(k-1);j-=2){
ans[2*i][j]='.';
ans[2*i+2][j]='.';
}
ans[2*i+1][2*m-k]='.';
k=0;
}
if(2*i+3<2*n+1) ans[2*i+3][2*m]='.';
}
if(k){
if(m%2==0&&k==m-1){
cout<<"No"<<endl;
return 0;
}
int i=n-1;
for(int j=1;j<n-1&&k;j+=2){
ans[i*2][j*2+1]='|';
ans[i*2+1][j*2]=ans[i*2+1][j*2+2]=ans[i*2+2][j*2+1]='.';
k-=2;
}
}
cout<<"Yes"<<endl;
for(int i=1;i<=2*n+1;i++){
for(int j=1;j<=2*m+1;j++)
cout<<ans[i][j];
cout<<endl;
}
return 0;
}