为了检验电机仿真模型的正确性,,以基于s函数方法搭建的数学模型为例,搭建如图的三相所示的简单三相PMSM矢量控制系统,此模型忽略了PWM逆变器的影响。另外,感兴趣的同志可以对基于Simulink方法搭建的仿真模型进行验证。
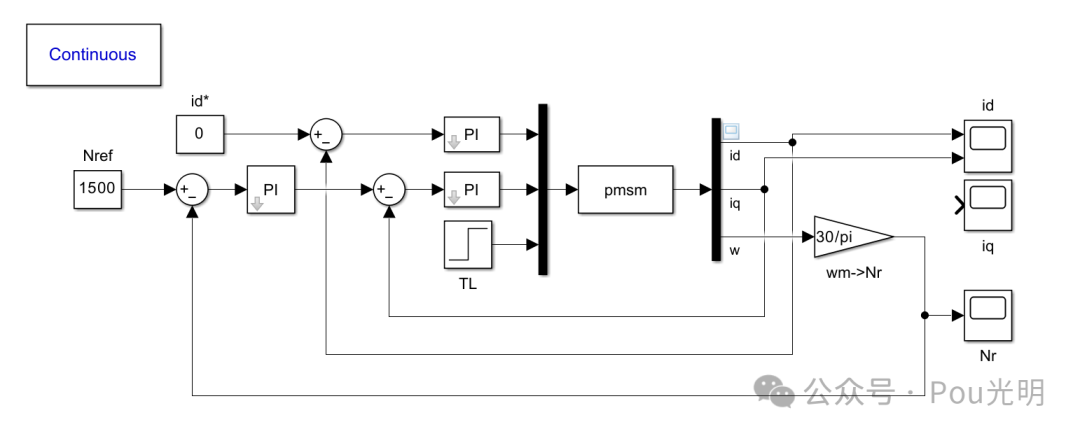
图中三相PMSM的数学模型采用MATLAB/Simulink中User-DefinedFunctions中的S-Function模块,该模块的具体设置如下。其中:pmsm为s函数的函数名;电机的参数设置为:极对数pn=4,定子电感Lq=Ld=8.5mH,定子电阻R=2.875Ω,磁链φf=0.175Wb,转动惯量J=0.001kg.m*m,阻尼系数B=0.008N.m.s。
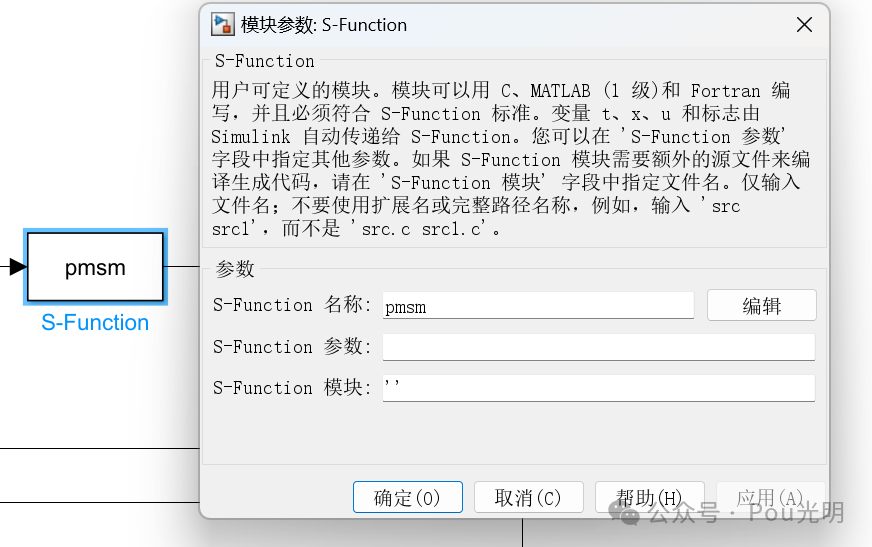
采用s函数方法的三相PMSM数学模型的程序编写和函数说明如下:
function [sys,x0,str,ts] = pmsm(t,x,u,flag)
switch flag,
%%%%%%%%%%%%%%%%%%
% Initialization %
%%%%%%%%%%%%%%%%%%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
function sys=mdlDerivatives(t,x,u)
R = 2.875;
Ld = 8.5e-3;
Lq =8.5e-3;
Pn = 4;
Phi = 0.175;
J = 0.001;
B = 0.008;
sys(1)=(1/Ld)*u(1)-(R/Ld)*x(1)+(Lq/Ld)*Pn*x(2)*x(3);
%对应微分方程(1-27)
sys(2)=(1/Lq)*u(2)-(R/Lq)*x(2)-(Ld/Lq)*Pn*x(3)*x(2)-(Phi*Pn/Lq)*x(3);
%对应微分方程(1-27)
sys(3)=(1/J)*(1.5*Pn*(Phi*x(2)+(Ld-Lq)*x(2)*x(3))-B*x(3)-u(3));
%对应微分方程(1-28)采用上述的矢量控制策略,仿真模型中转速PI调节器和电流环PI调节器参数设置如图所示。其中,PI调节器采用离散型调节器。
另外,值得说明的是Sample time设置为Ts,打开【建模】->【模型设置】->【模型属性】,具体参数如图。从图中可以看出,采用模型属性中的初始化函数,特别是当控制器的参数较多时,该方法便于后期控制器参数的整定,以后搭建模型时可以采用此种方法进行参数设置。
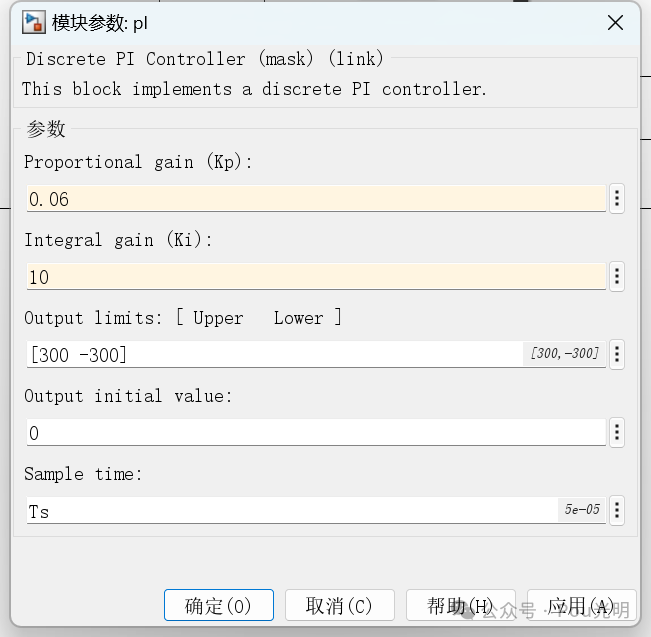
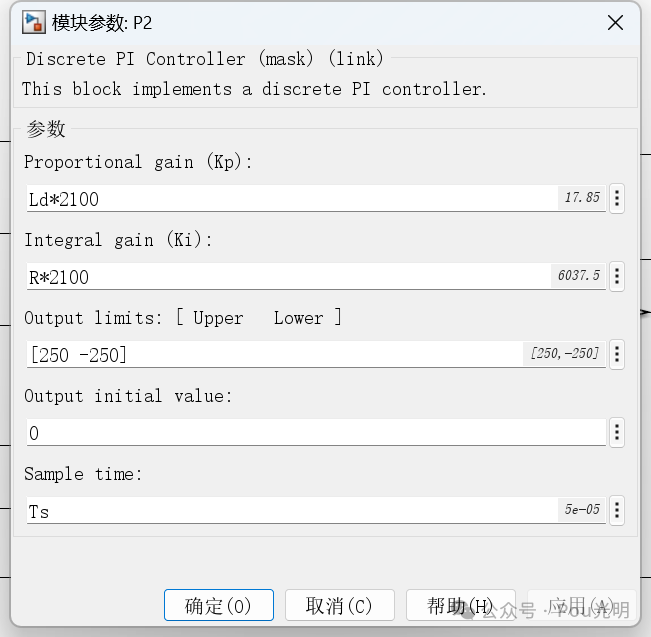
为了验证仿真模型的正确性,仿真条件设置为:参考转速1500r/min,负载转矩TL初始值设置为0,当t=0.05s时TL=10N.m。仿真结果如下,可以看出,电机实际转速能够快速跟踪参考转速,d-q轴定子电流也有较快的动态响应速度, 从而验证仿真模型的正确性。
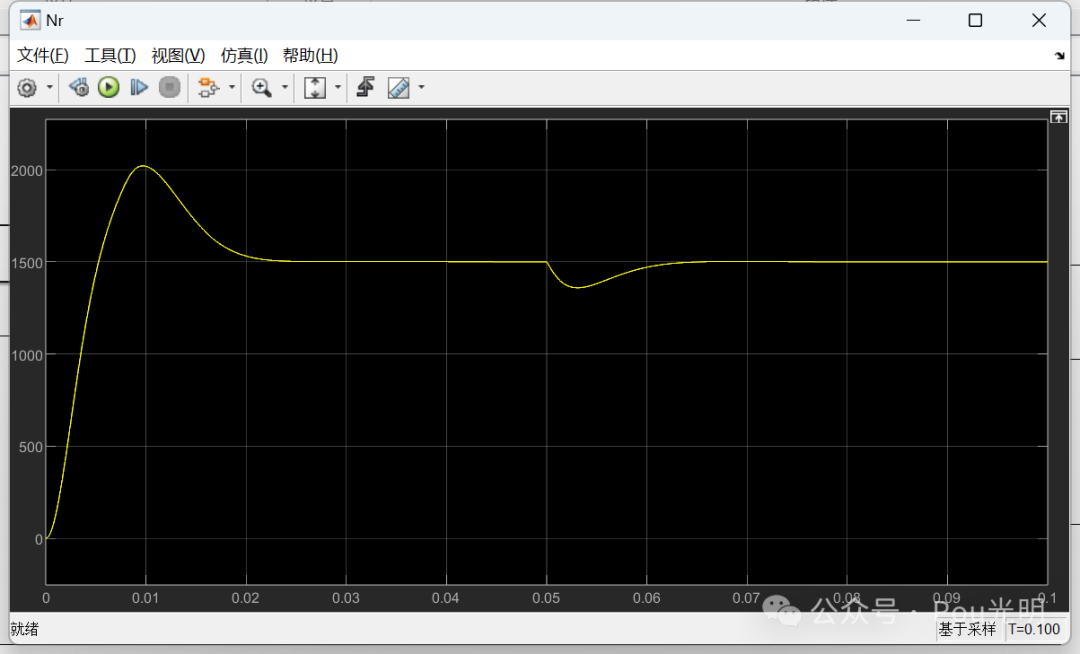
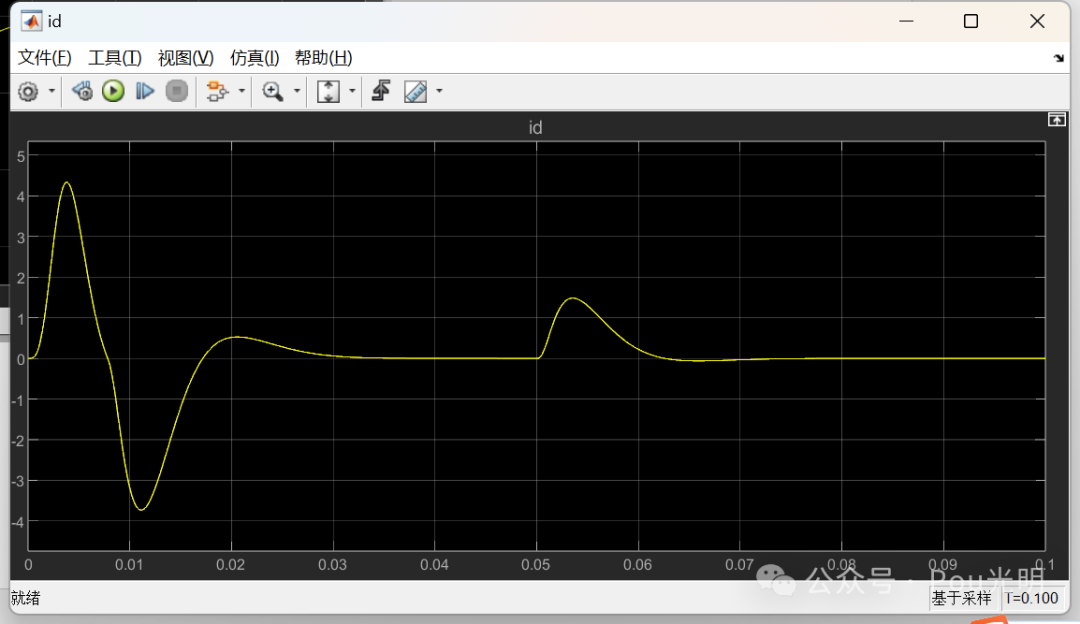
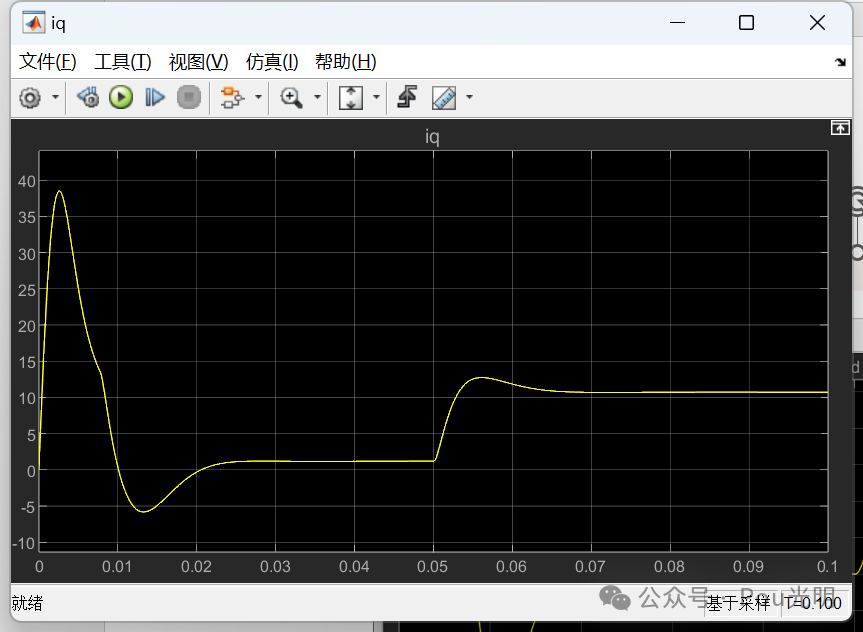
本次介绍到这,需要matlab程序的小伙伴可在后台留言”s函数仿真”。