一、题目描述

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words， 返回所有二维网格上的单词 。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：

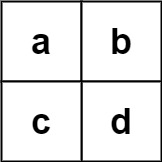
输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] 是一个小写英文字母
• 1 <= words.length <= 3 * 10^4
• 1 <= words[i].length <= 10
• words[i] 由小写英文字母组成
• words 中的所有字符串互不相同

二、解题思路

这个问题可以使用深度优先搜索（DFS）结合前缀树（Trie）来解决。首先，我们构建一个前缀树，将所有的单词插入到前缀树中。然后，我们遍历二维网格的每一个单元格，从每个单元格开始，使用深度优先搜索在网格中寻找匹配前缀树的单词。

以下是具体的步骤：

1. 构建前缀树：创建一个Trie类，包含插入和查找方法。将所有的单词插入到前缀树中。

2. 深度优先搜索：创建一个DFS方法，该方法接受当前单元格的位置、前缀树节点、网格、以及已经访问过的单元格集合。在DFS过程中，如果当前单元格的字符不在前缀树中，返回；否则，检查当前节点是否是一个单词的结尾，如果是，则将该单词添加到结果集中，并从前缀树中删除该单词，以避免重复添加。

3. 遍历网格：遍历网格的每一个单元格，从每个单元格开始进行DFS搜索。

三、具体代码

class Solution {
    class TrieNode {
        TrieNode[] children = new TrieNode[26];
        String word;
    }

    class Trie {
        TrieNode root = new TrieNode();

        public void insert(String word) {
            TrieNode node = root;
            for (char c : word.toCharArray()) {
                if (node.children[c - 'a'] == null) {
                    node.children[c - 'a'] = new TrieNode();
                }
                node = node.children[c - 'a'];
            }
            node.word = word;
        }
    }

    public List<String> findWords(char[][] board, String[] words) {
        Trie trie = new Trie();
        for (String word : words) {
            trie.insert(word);
        }
        List<String> res = new ArrayList<>();
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                dfs(board, i, j, trie.root, res);
            }
        }
        return res;
    }

    private void dfs(char[][] board, int i, int j, TrieNode node, List<String> res) {
        if (i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] == '#' || node.children[board[i][j] - 'a'] == null) {
            return;
        }
        char c = board[i][j];
        node = node.children[c - 'a'];
        if (node.word != null) {
            res.add(node.word);
            node.word = null; // 避免重复添加
        }
        board[i][j] = '#'; // 标记为已访问
        dfs(board, i - 1, j, node, res);
        dfs(board, i + 1, j, node, res);
        dfs(board, i, j - 1, node, res);
        dfs(board, i, j + 1, node, res);
        board[i][j] = c; // 恢复现场
    }
}

在上述代码中，我们首先构建了一个Trie树，然后通过DFS在网格中搜索匹配的单词。在DFS过程中，我们使用#字符来标记已经访问过的单元格，以避免重复访问。当一个单词被找到时，我们从Trie树中移除该单词，确保不会重复添加到结果集中。最后，我们恢复单元格的原始字符，以便其他搜索路径可以使用该单元格。

四、时间复杂度和空间复杂度

1. 时间复杂度

• 构建Trie树：

  • 对于每个单词，我们遍历其所有字符并将其插入到Trie树中。假设单词列表words中总共有N个单词，每个单词的平均长度为L，则构建Trie树的时间复杂度为O(N * L)。

• 深度优先搜索（DFS）：

  • 对于网格中的每个单元格，我们可能都会执行一次DFS搜索。网格大小为m * n，每个单元格最多会被访问4次（上、下、左、右）。
  • 在最坏的情况下，每次DFS搜索都会遍历整个网格，即每次DFS的时间复杂度为O(m * n)。
  • 因此，所有DFS搜索的总时间复杂度为O(m * n * 4 * m * n)，即O(4 * m^2 * n^2)，简化后为O(m^2 * n^2)。

综上所述，总的时间复杂度为构建Trie树的时间复杂度加上DFS的时间复杂度，即O(N * L + m^2 * n^2)。

2. 空间复杂度

• Trie树：

  • Trie树的空间复杂度取决于单词的数量和长度。在最坏的情况下，如果所有单词都是独特的，Trie树将包含所有单词的字符，空间复杂度为O(N * L)。

• DFS搜索：

  • DFS搜索需要递归栈空间，在最坏的情况下，递归深度为网格大小m * n，因此递归栈空间复杂度为O(m * n)。

• 结果列表：

  • 结果列表存储找到的单词，其空间复杂度取决于找到的单词数量，但不会超过单词列表的总数N，因此空间复杂度为O(N)。

综上所述，总的空间复杂度为Trie树的空间复杂度加上DFS递归栈的空间复杂度加上结果列表的空间复杂度，即O(N * L + m * n + N)。由于N * L通常是最大的，因此可以简化为O(N * L)。

五、总结知识点

• 数据结构 - Trie树（前缀树）：

  • Trie树是一种用于检索字符串数据集中的键的有序树结构，是一种高效的字符串查找数据结构。
  • 每个节点包含一个字符数组children，用于存储子节点，子节点的索引对应字符与’a’的差值。
  • 每个节点可能包含一个字符串word，用于标记该节点是否是某个单词的结束。

• 递归 - 深度优先搜索（DFS）：

  • DFS是一种用于遍历或搜索树或图的算法。
  • 在DFS中，代码通过递归函数dfs来探索所有可能的路径。
  • DFS的递归终止条件包括越界检查、已访问标记检查以及当前字符是否存在于Trie树中的子节点。

• 字符串处理：

  • 字符串转换为字符数组word.toCharArray()，以便遍历字符串中的每个字符。
  • 字符到索引的转换c - 'a'，用于访问Trie树中相应的子节点。

• 数组操作：

  • 使用二维字符数组board表示网格。
  • 数组索引访问，例如board[i][j]，用于访问网格中的单元格。

• 集合操作：

  • 使用List<String>来存储找到的单词。
  • 使用ArrayList作为具体的列表实现，提供动态数组的功能。

• 逻辑控制：

  • if语句用于条件判断，例如检查边界条件、字符是否匹配Trie树节点。
  • for循环用于遍历网格的每个单元格和单词列表的每个单词。

• 标记与恢复：

  • 使用特殊字符'#'来标记网格中的单元格已被访问，防止在DFS中重复访问。
  • 在完成当前路径的搜索后，恢复单元格的原始字符，以便其他路径可以使用该单元格。

• 代码优化：

  • 在找到单词后，立即将Trie树中对应节点的word字段设置为null，避免在后续搜索中重复添加相同的单词。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。