nefu暑假acm集训1 构造矩阵个人模板+例题汇总

前言：

以下都是nefu暑假集训的训练题，我在此把我的模板和写的一些练习题汇总一下并分享出来，希望在能满足我复习的情况下能帮助到你。

正文：

模板：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=mod;
typedef struct{
	ll m[n][n];//一个n*n的矩阵，注意矩阵不能太大，若太大则不能给他写成结构 
}; 
matrix P={
	//内部填写自己经过推导构造出来的矩阵 
};
matrix I={
	//内部填写自相应大小的单位矩阵 
};
matrix mul(matrix a,matrix b){//对两个大小为n*n的矩阵进行相乘并取模操作 
	matrix c;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			c.m[i][j]=0;
			for(int k=0;k<n;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){//对矩阵进行快速幂操作 
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}

这是矩阵连乘的基础模板

习题：

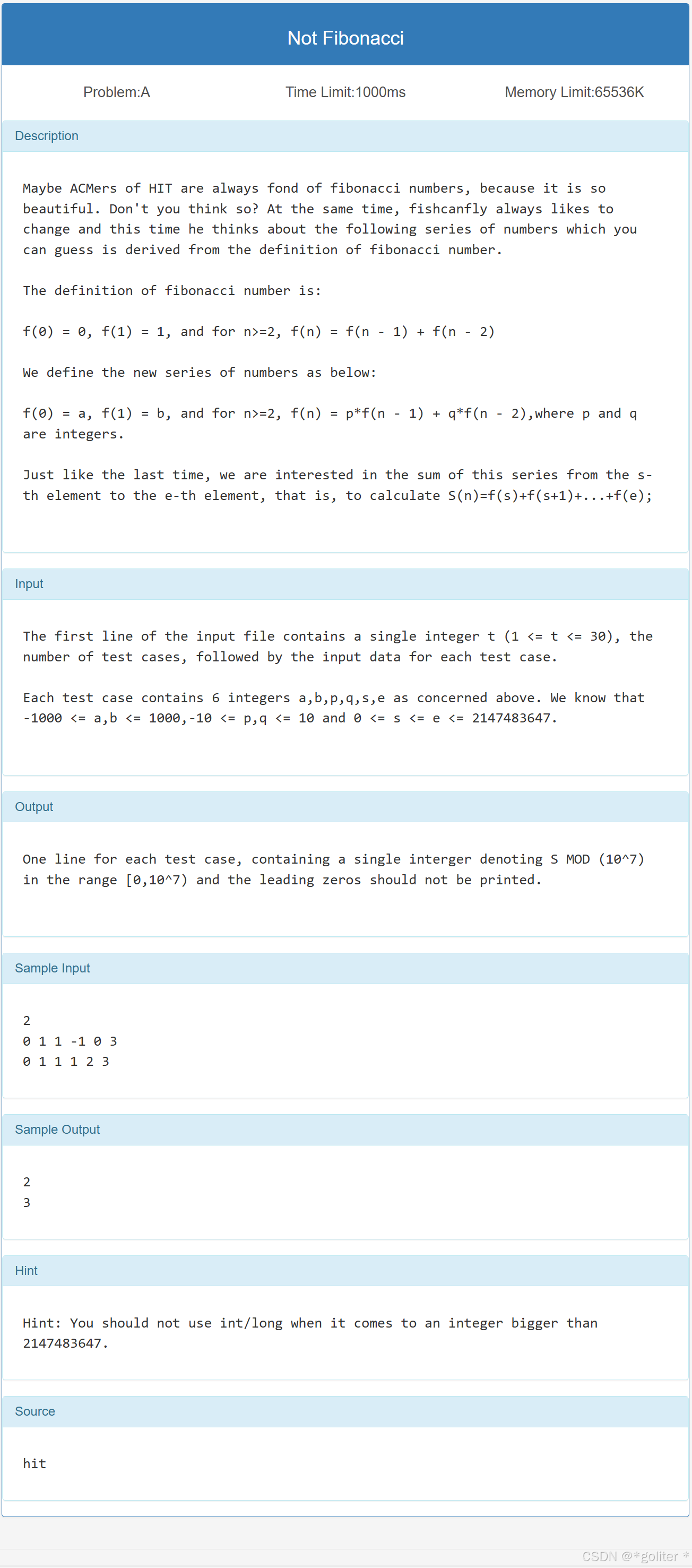
1、Not Fibonacci：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e7;
typedef struct{
	ll m[3][3];
}matrix;
matrix P={
	0,0,0,
	1,0,0,
	0,0,1
};
matrix I={
	1,0,0,
	0,1,0,
	0,0,1
};
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			c.m[i][j]=0;
			for(int k=0;k<3;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}
ll a,b,p,q,s,e;
int main(){
	int t;
	cin>>t;
	while(t--){
		ll l,r;
		matrix tmp;
		cin>>a>>b>>p>>q>>s>>e;
		P.m[0][0]=p;P.m[0][1]=q; 
 		P.m[2][0]=p;P.m[2][1]=q;
 		if(e==0)r=(a%mod+mod)%mod;
 		else if(e==1)r=((a+b)%mod+mod)%mod;
 		else{
 			tmp=quickpow(e-1);
 			r=(tmp.m[2][0]*b)%mod+(tmp.m[2][1]*a)%mod+(tmp.m[2][2]*(a+b))%mod;
 			r=(r%mod+mod)%mod;
		}
		if(s==0)l=0;
		else if(s==1)l=a;
		else if(s==2)l=((a+b)%mod+mod)%mod;
		else{
			tmp=quickpow(s-2);
 			l=(tmp.m[2][0]*b)%mod+(tmp.m[2][1]*a)%mod+(tmp.m[2][2]*(a+b))%mod;
 			l=(l%mod+mod)%mod;
		}
		cout<<((r-l)%mod+mod)%mod<<endl;
	}
	return 0;
}

构造出相应的p矩阵为 $\begin{vmatrix} p & q& 0\\ 1 &0 &0 \\ p &q &1 \end{vmatrix}$ ，初始矩阵为 $\begin{vmatrix} a_{n}\\ a_{n-1}\\ s_{n}\end{vmatrix}$ ，在根据s,e分别计算即可。

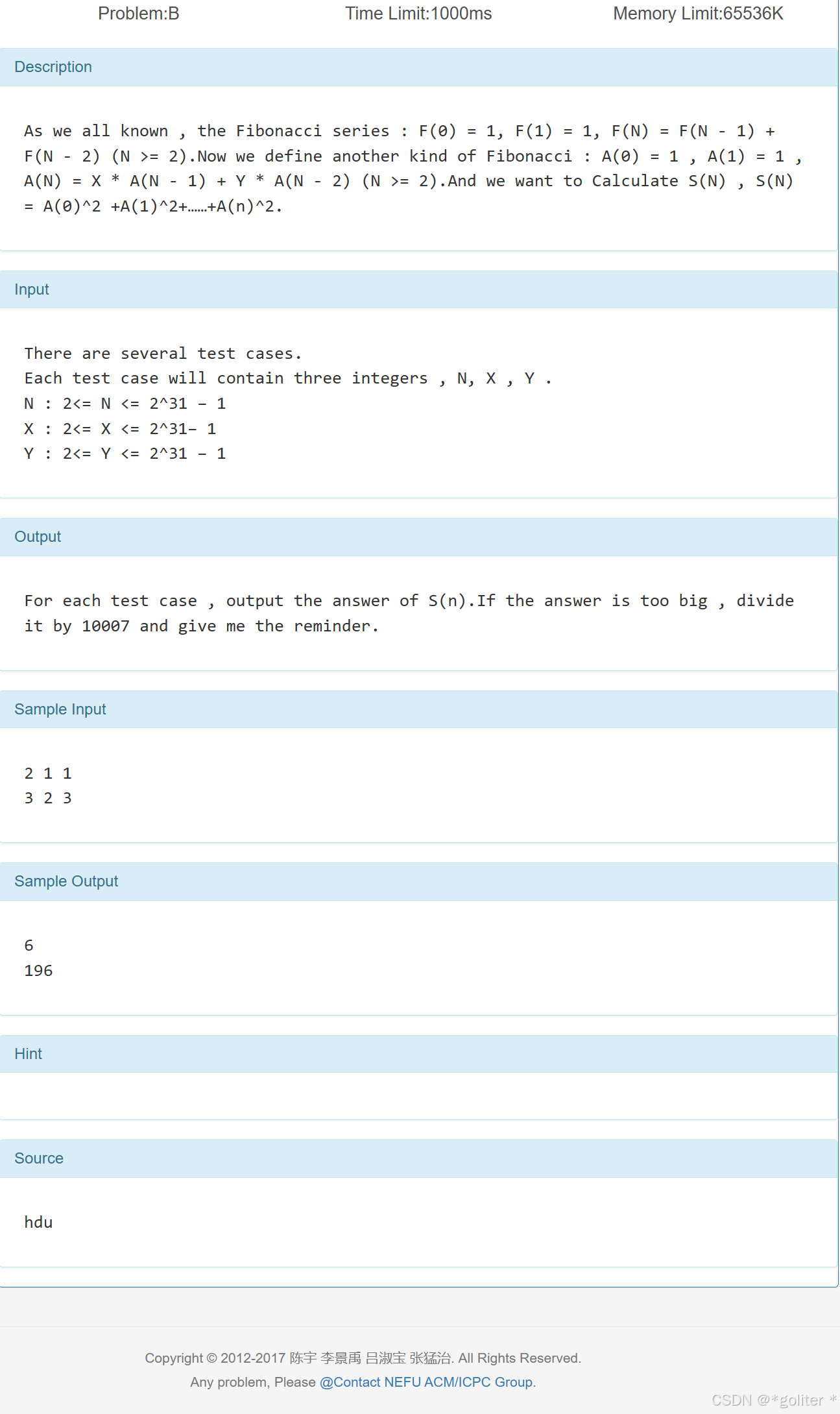
2、Another kind of Fibonacci

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=10007;
typedef struct{
	ll m[4][4];
}matrix;
matrix P={
	1,0,0,0,
	0,0,0,0,
	0,0,0,0,
	0,1,0,0
};
matrix I={
	1,0,0,0,
	0,1,0,0,
	0,0,1,0,
	0,0,0,1
};
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<4;i++){
		for(int j=0;j<4;j++){
			c.m[i][j]=0;
			for(int k=0;k<4;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}
ll n,x,y;
int main(){
	while(cin>>n>>x>>y){
		ll sum;
		P.m[0][1]=x*x%mod;P.m[0][2]=2*x*y%mod;P.m[0][3]=y*y%mod;
		P.m[1][1]=x*x%mod;P.m[1][2]=2*x*y%mod;P.m[1][3]=y*y%mod;
		P.m[2][1]=x%mod;P.m[2][2]=y%mod;
		if(n==0)sum=1;
		else if(n==1)sum=2;
		else{
			matrix tmp=quickpow(n-1);
			sum=(tmp.m[0][0]*2%mod)+(tmp.m[0][1]%mod)+(tmp.m[0][2]%mod)+(tmp.m[0][3]%mod);
			sum=(sum%mod+mod)%mod;
		}
		cout<<sum<<endl;
	}
	return 0;
}

上题的稍难版，不过核心还是推矩阵p和初始矩阵，得出来便可以直接代入模板。

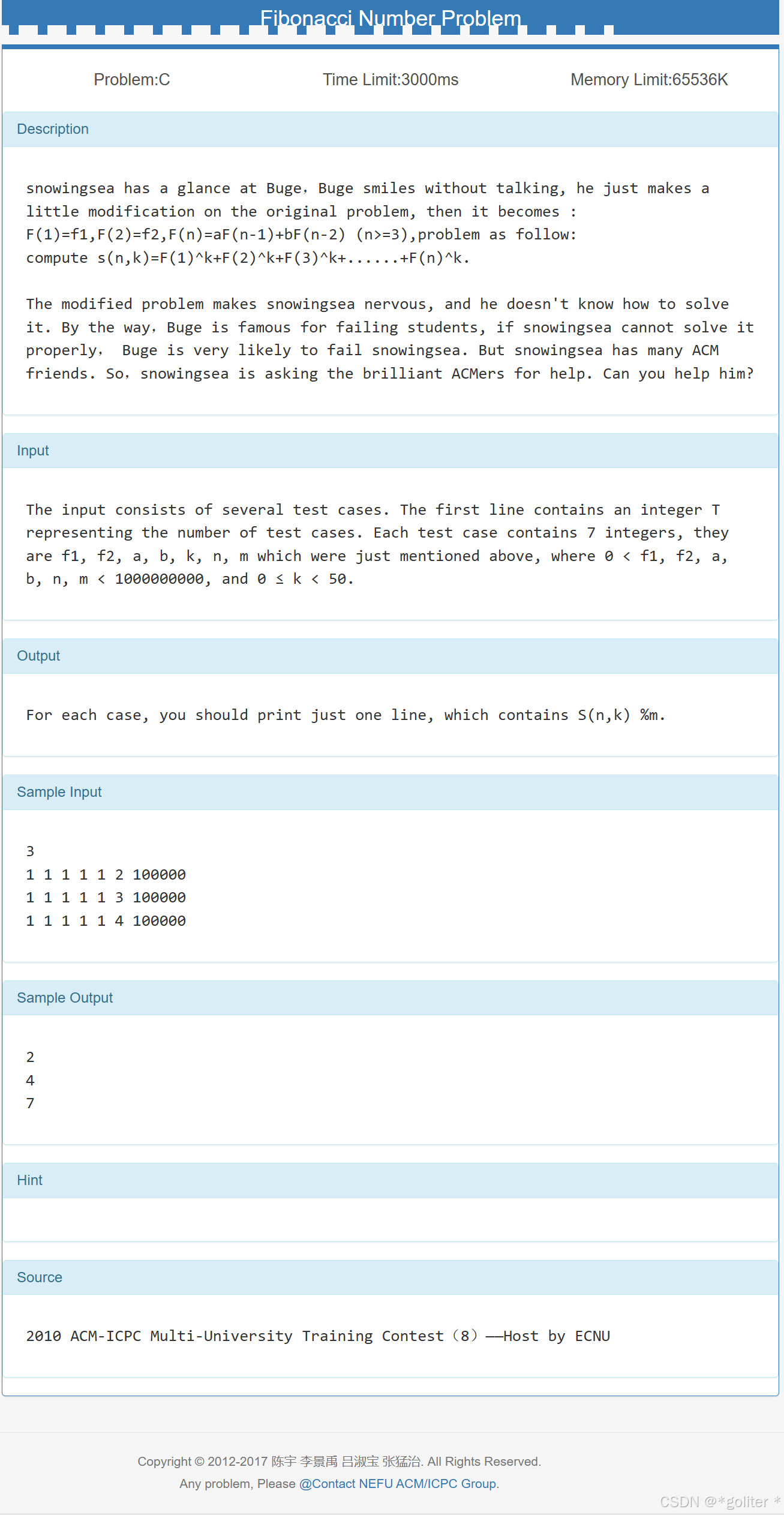
3、Fibonacci Number Problem

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 54;
LL mod, size;//size = 矩阵大小
typedef struct
{
    LL m[maxn][maxn];
} Matrix;

Matrix P;
Matrix I;
//正常快速幂
LL quick_mod(LL a, LL b, LL c)
{
    LL ans = 1;
    if(b == 0)
        return 1;
    while(b)
    {
        if(b & 1)
            ans = (ans*a)%c;
        b >>= 1;
        a = (a*a)%c;
    }
    return ans;
}
//矩阵乘法
Matrix matrix_mul(Matrix a, Matrix b)
{
    int i, j, k;
    Matrix c;
    for(i=0; i<size; i++)
    {
        for(j=0; j<size; j++)
        {
            c.m[i][j] = 0;
            for(k=0; k<size; k++)
            {
                c.m[i][j] += ((a.m[i][k]%mod)*(b.m[k][j]%mod))%mod;
            }
            c.m[i][j] %= mod;
        }
    }
    return c;
}
//矩阵的快速幂
Matrix quick_pow(LL m)
{
    Matrix b=P, ans=I;
    while(m)
    {
        if(m & 1)
            ans = matrix_mul(ans, b);
        m >>= 1;
        b = matrix_mul(b, b);
    }
    return ans;
}
//组合数。。。
LL c[50][50];
int main()
{
    memset(c, 0, sizeof(c));
    for(int i=0; i<50; i++)
    {
        c[i][0] = 1;
        c[i][i] = 1;
    }
    for(int i=1; i<50; i++)
        for(int j=1; j<i; j++)
            c[i][j] = c[i-1][j] + c[i-1][j-1];
    int t;
    Matrix tmp;
    LL f1, f2, a, b, k, n, m ;
    LL sum, ans1, ans2;
    //scanf("%d",&t);
    cin>>t;
    while(t--)
    {
        sum = 0;
        cin>>f1>>f2>>a>>b>>k>>n>>mod;
        //scanf("%lld%lld%lld%lld%lld%lld%lld",&f1,&f2,&a,&b,&k,&n,&mod);
        memset(P.m, 0, sizeof(P.m));
        memset(I.m, 0, sizeof(I.m));
        if(k == 0)
            printf("%lld\n",n%mod);
        else
        {
            if(n == 1)
                cout<<quick_mod(f1, k, mod)<<endl;
            else if(n == 2)
                cout<<(quick_mod(f1,k,mod) + quick_mod(f2,k,mod))%mod<<endl;
            else
            {
                size = k+2;
                //矩阵赋值
                for(int i=0; i<size; i++)
                    I.m[i][i] = 1;
                P.m[0][0] = 1;
                P.m[0][size-1] = 1;
                for(int i=1; i<size-1; i++)
                    P.m[0][i] = 0;
                for(int i=1; i<size; i++)
                    for(int j=size-i,w=0; j<size; j++,w++)
                    {
                        P.m[i][j]=(((c[i-1][w]%mod)*quick_mod(a,w,mod))%mod)*quick_mod(b,i-1-w,mod);
                        P.m[i][j] %= mod;
                    }
                tmp = quick_pow(n-1);
                sum = (sum+(tmp.m[0][0]%mod)*(quick_mod(f1,k,mod)))%mod;
                for(int i=1; i<size; i++)
                {
                    ans1 = (quick_mod(f1,size-1-i,mod)*quick_mod(f2,i-1,mod))%mod;
                    ans2 = (ans1*(tmp.m[0][i]%mod))%mod;
                    sum = (sum+ans2)%mod;
                }
                cout<<sum%mod<<endl;
            }
        }
    }
    return 0;
}

首先一个难题就是怎么判断矩阵的维数（矩阵的维数是个变量），解决方法：开一个比较大的数组，然后再用一个公有变量记一下就行了，具体详见代码；
矩阵k次方是啥，找规律来求解；

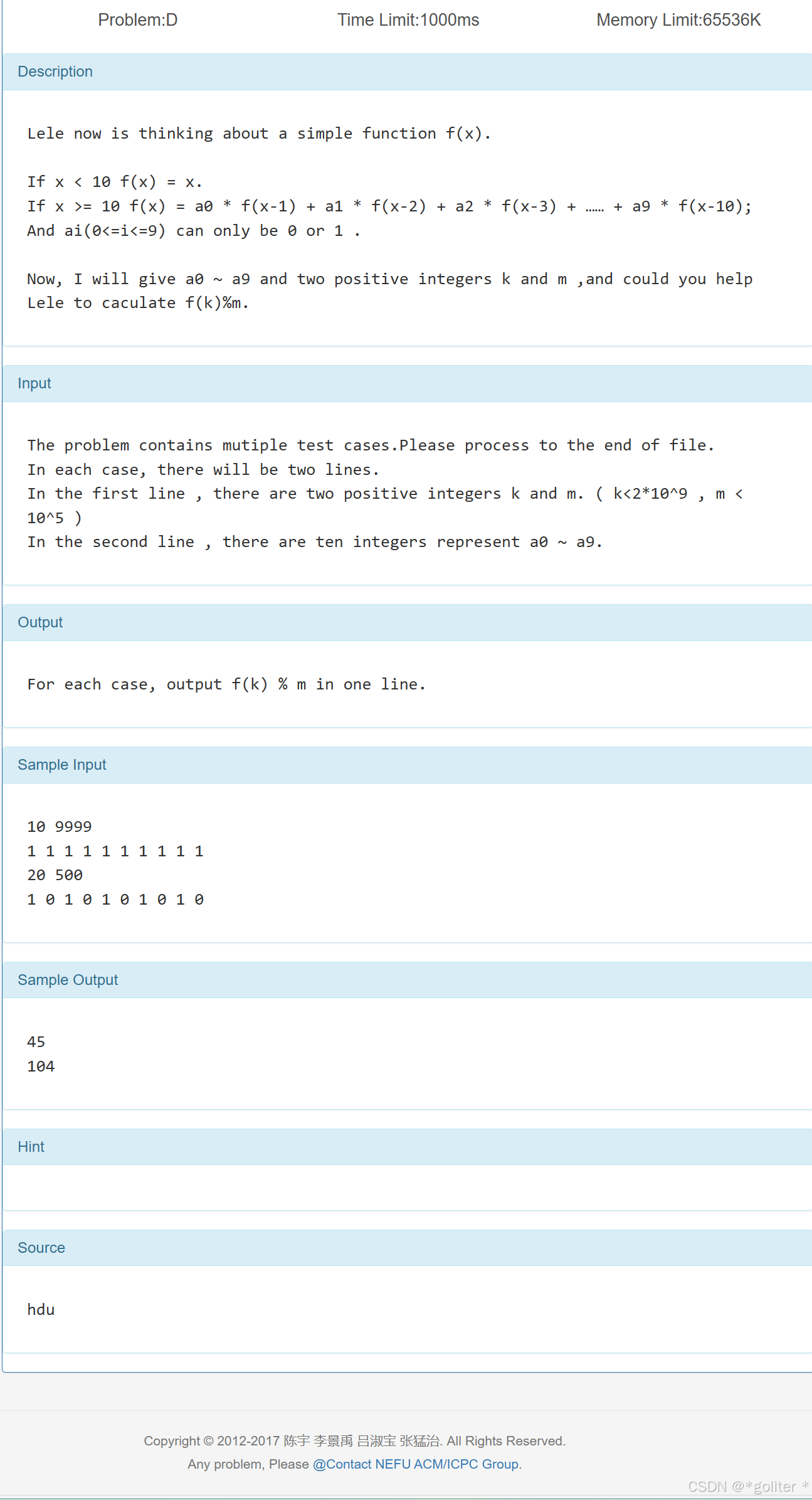
4、A Simple Math Problem

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef struct{
	ll m[10][10];
}matrix;
matrix P={
	0,0,0,0,0,0,0,0,0,0,
	1,0,0,0,0,0,0,0,0,0,
	0,1,0,0,0,0,0,0,0,0,
	0,0,1,0,0,0,0,0,0,0,
	0,0,0,1,0,0,0,0,0,0,
	0,0,0,0,1,0,0,0,0,0,
	0,0,0,0,0,1,0,0,0,0,
	0,0,0,0,0,0,1,0,0,0,
	0,0,0,0,0,0,0,1,0,0,
	0,0,0,0,0,0,0,0,1,0
};
matrix I={
	1,0,0,0,0,0,0,0,0,0,
	0,1,0,0,0,0,0,0,0,0,
	0,0,1,0,0,0,0,0,0,0,
	0,0,0,1,0,0,0,0,0,0,
	0,0,0,0,1,0,0,0,0,0,
	0,0,0,0,0,1,0,0,0,0,
	0,0,0,0,0,0,1,0,0,0,
	0,0,0,0,0,0,0,1,0,0,
	0,0,0,0,0,0,0,0,1,0,
	0,0,0,0,0,0,0,0,0,1
};
int k,m;
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<10;i++){
		for(int j=0;j<10;j++){
			c.m[i][j]=0;
			for(int k=0;k<10;k++){
				a.m[i][k]=(a.m[i][k]%m+m)%m; 
				b.m[k][j]=(b.m[k][j]%m+m)%m; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%m;
			}
			c.m[i][j] = (c.m[i][j]%m+m)%m;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}

int main(){
	while(cin>>k>>m){
		cin>>P.m[0][0]>>P.m[0][1]>>P.m[0][2]>>P.m[0][3]>>P.m[0][4]>>P.m[0][5]>>P.m[0][6]>>P.m[0][7]>>P.m[0][8]>>P.m[0][9];
		ll sum;
		if(k<10){
			sum=k%m;
		}
		else{
			matrix tmp=quickpow(k-9);
			sum=(tmp.m[0][0]*9)%m+(tmp.m[0][1]*8)%m+(tmp.m[0][2]*7)%m+(tmp.m[0][3]*6)%m+(tmp.m[0][4]*5)%m+(tmp.m[0][5]*4)%m+(tmp.m[0][6]*3)%m+(tmp.m[0][7]*2)%m+(tmp.m[0][8])%m;
			sum=(sum%m+m)%m;
		}
		cout<<sum<<endl;
	}
	return 0;
}

矩阵稍大稍微有点麻烦，不过还是可以直接写出来的。

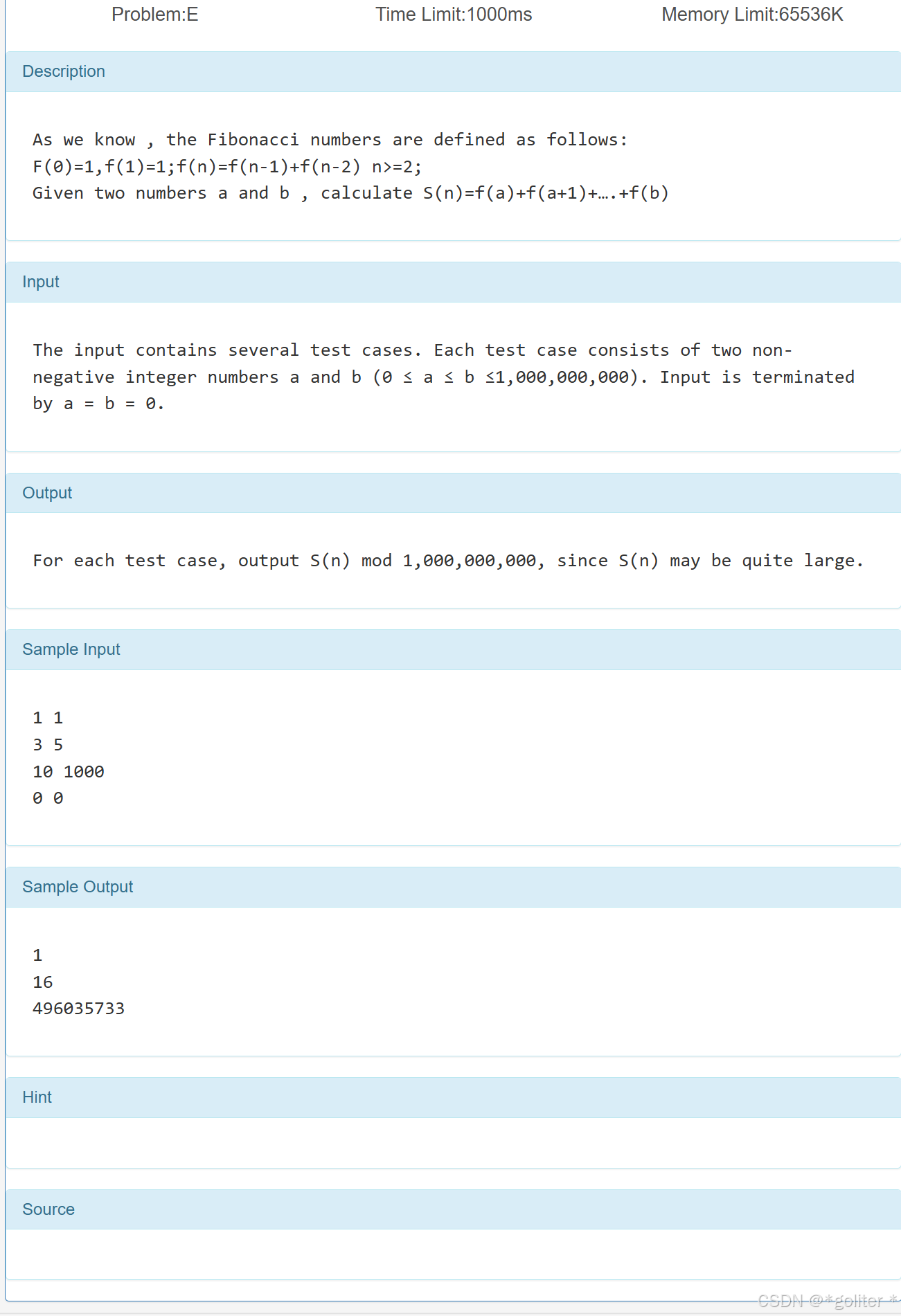
5、Fibs之和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9;
typedef struct{
	ll m[3][3];
}matrix;
matrix P={
	0,0,0,
	1,0,0,
	0,0,1
};
matrix I={
	1,0,0,
	0,1,0,
	0,0,1
};
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			c.m[i][j]=0;
			for(int k=0;k<3;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}
ll a,b,p,q,s,e;
int main(){
	while(cin>>s>>e){
		if(s==0&&e==0)break;
		ll l,r;
		matrix tmp;
		P.m[0][0]=1;P.m[0][1]=1; 
 		P.m[2][0]=1;P.m[2][1]=1;
 		if(e==0)r=1;
 		else if(e==1)r=2;
 		else{
 			tmp=quickpow(e-1);
 			r=(tmp.m[2][0])%mod+(tmp.m[2][1])%mod+(tmp.m[2][2])%mod;
 			r=(r%mod+mod)%mod;
		}
		if(s==0)l=0;
		else if(s==1)l=1;
		else if(s==2)l=2;
		else{
			tmp=quickpow(s-2);
 			l=(tmp.m[2][0])%mod+(tmp.m[2][1])%mod+(tmp.m[2][2])%mod;
 			l=(l%mod+mod)%mod;
		}
		cout<<((r-l)%mod+mod)%mod<<endl;
	}
	return 0;
}

和1一摸一样

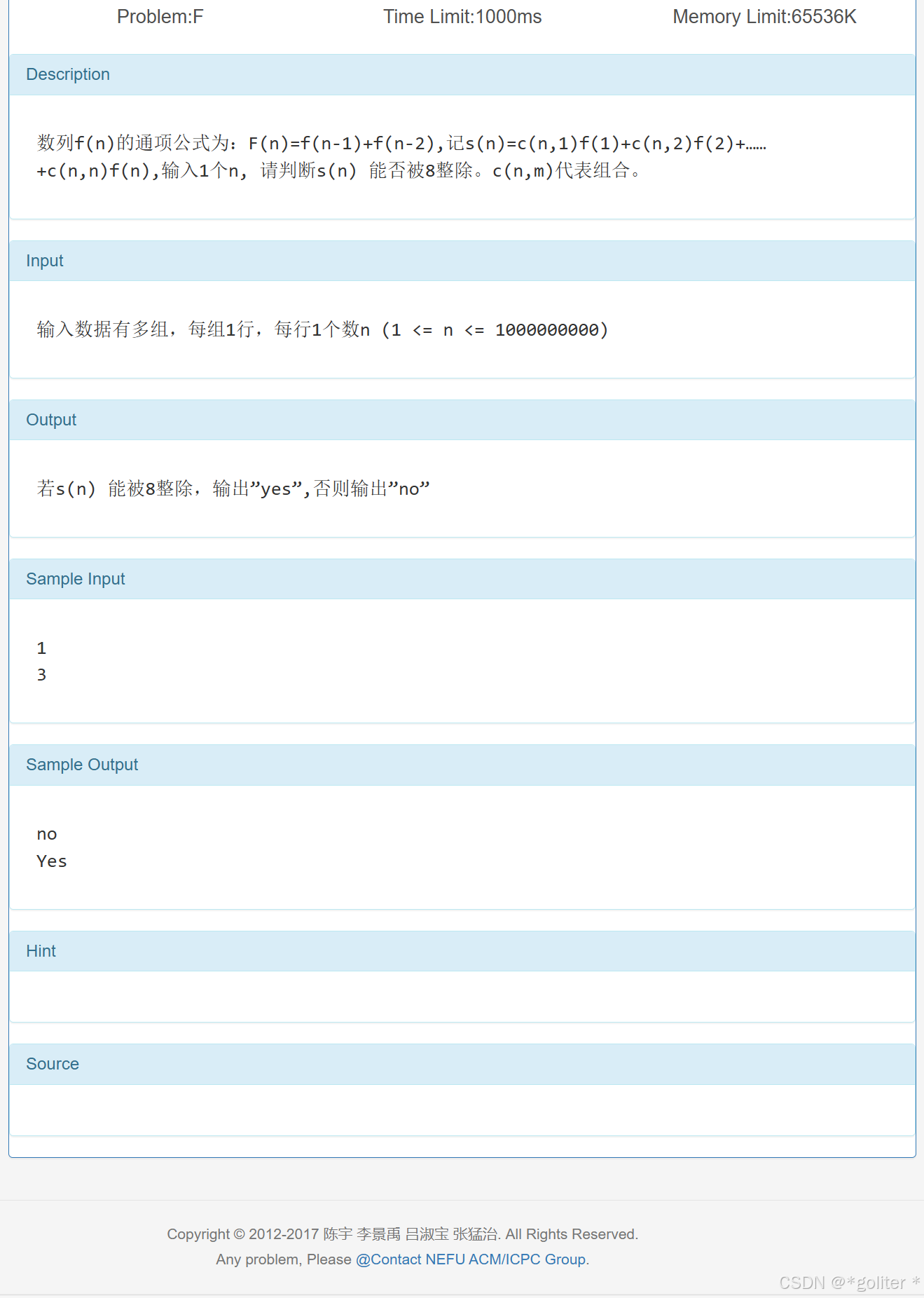
6、fibs的组合

#include<bits/stdc++.h>
using namespace std;
int main(){
	int n;
	while(cin>>n){
		if(n%3==0){
		cout<<"yes"<<endl;
		}	
		else{
		cout<<"no"<<endl;
	}
	}
	return 0;
}

找规律

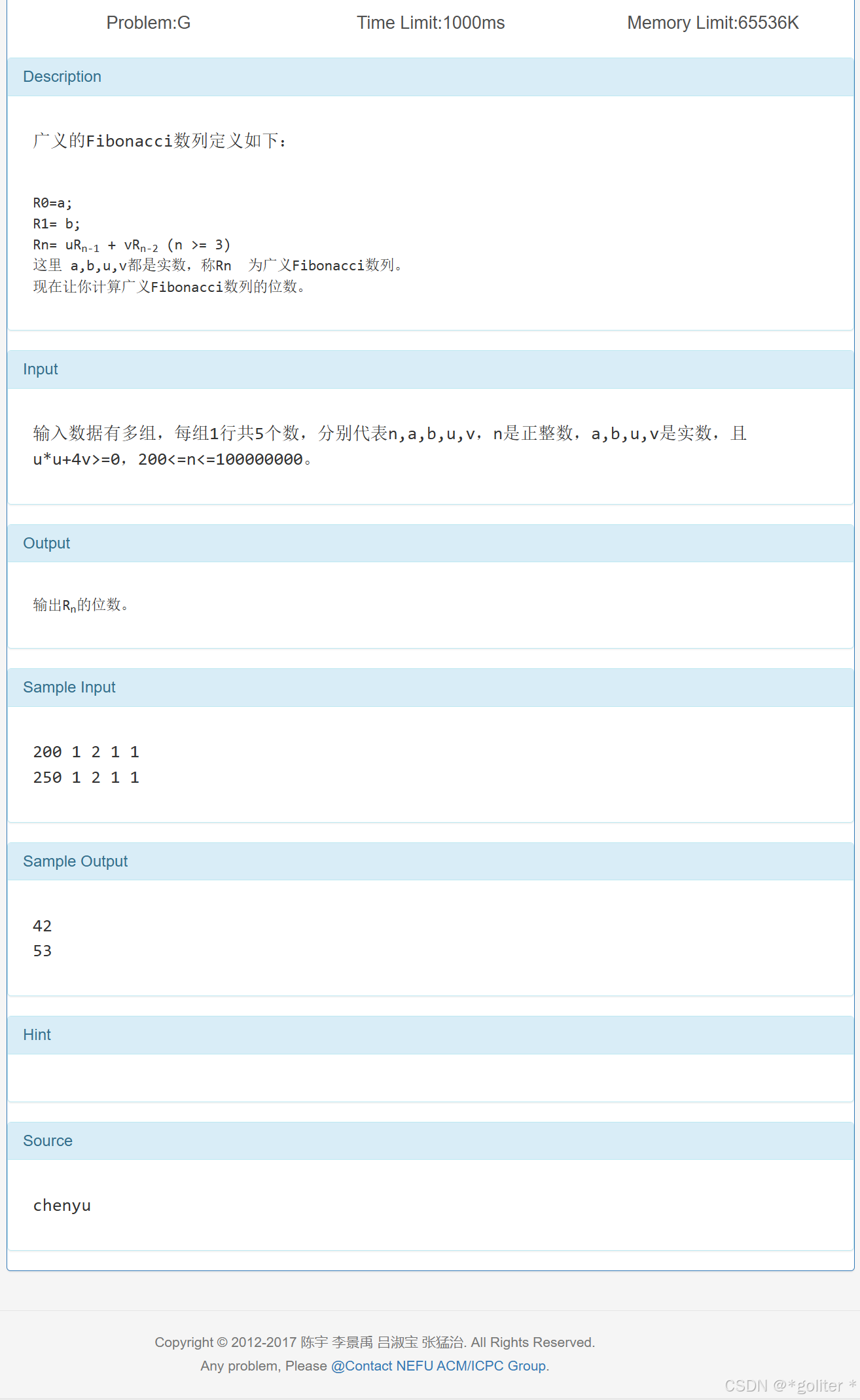
7、fibs的位数

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long n,a,b,u,v;
    while(scanf("%lld%lld%lld%lld%lld",&n,&a,&b,&u,&v)!=EOF)
    {
        double c=sqrt(u*u+4*v);
        double x=(u+c)/2.0;
        double y=(u-c)/2.0;
        double len=n*log10(x)+log10(b-a*y)-log10(c);
        printf("%lld\n",(long long)len+1);
    }
    return 0;
}

这个是纯概念（而且挺偏的），我感觉比赛不会有这种内容，想了解可以看看这个NEFU 461 fibs的位数()_现在让你计算广义fibonacci数列的位数。-CSDN博客

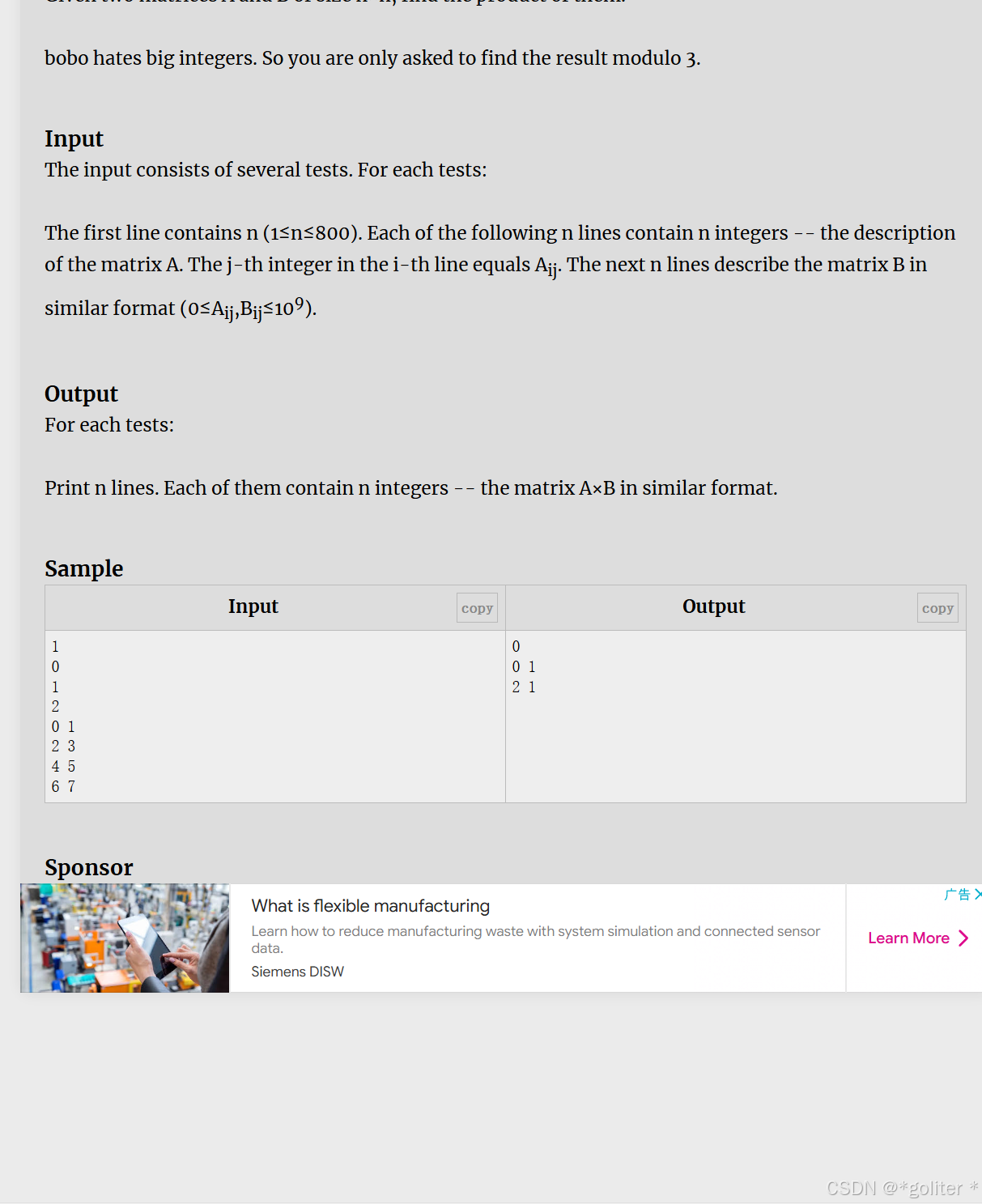
8、Matrix multiplication

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 817;
const int mod = 3;
int A[MAXN][MAXN], B[MAXN][MAXN];
int C[MAXN][MAXN];
int n;
 
int Scan()
{
	int res = 0, ch;
	ch=getchar();
	if(ch >= '0' && ch <= '9')		 
		res = ch - '0';
	while((ch = getchar()) >= '0' && ch <= '9' )
		res = res * 10 + ch - '0';
	return res;
}
 
void input()
{
	int i, j;
	for(i = 1; i <= n; i++)
	{
		for(j = 1; j <= n; j++)
		{
			//scanf("%d",&A[i][j]);
			//A[i][j] %= mod;
			A[i][j]=Scan()%3;
		}
	}
	for(i = 1; i <= n; i++)
	{
		for(j = 1; j <= n; j++)
		{
			//scanf("%d",&B[i][j]);
			//B[i][j] %= mod;
			B[i][j]=Scan()%3;
		}
	}
}
 
void multi()
{//两个相等矩阵的乘法，对于稀疏矩阵，有在0处不用运算的优化
	memset(C,0,sizeof(C));
	for(int i = 1; i <= n; i++)
	{
		for(int j = 1; j <= n; j++)
		{
			if(A[i][j] == 0)//稀疏矩阵优化
				continue;
			for(int k = 1; k <= n; k++)
			{
				C[i][k] += A[i][j]*B[j][k];//i行k列第j项
			//	C[i][k] %= mod;
			}
		}
	}
}
 
void print()//输出矩阵信息
{
	for(int i = 1; i <= n; i++)
	{
		for(int j = 1; j <= n; j++)
		{
			if(j == 1)
				printf("%d",C[i][j]%mod);
			else
				printf(" %d",C[i][j]%mod);
		}
		printf("\n");
	}
}
 
int main()
{
	while(~scanf("%d",&n))
	{
		input();
		multi();
		print();
	}
	return 0;
}

这题题目不难，但卡时间有一点刻意了，十分恶心。

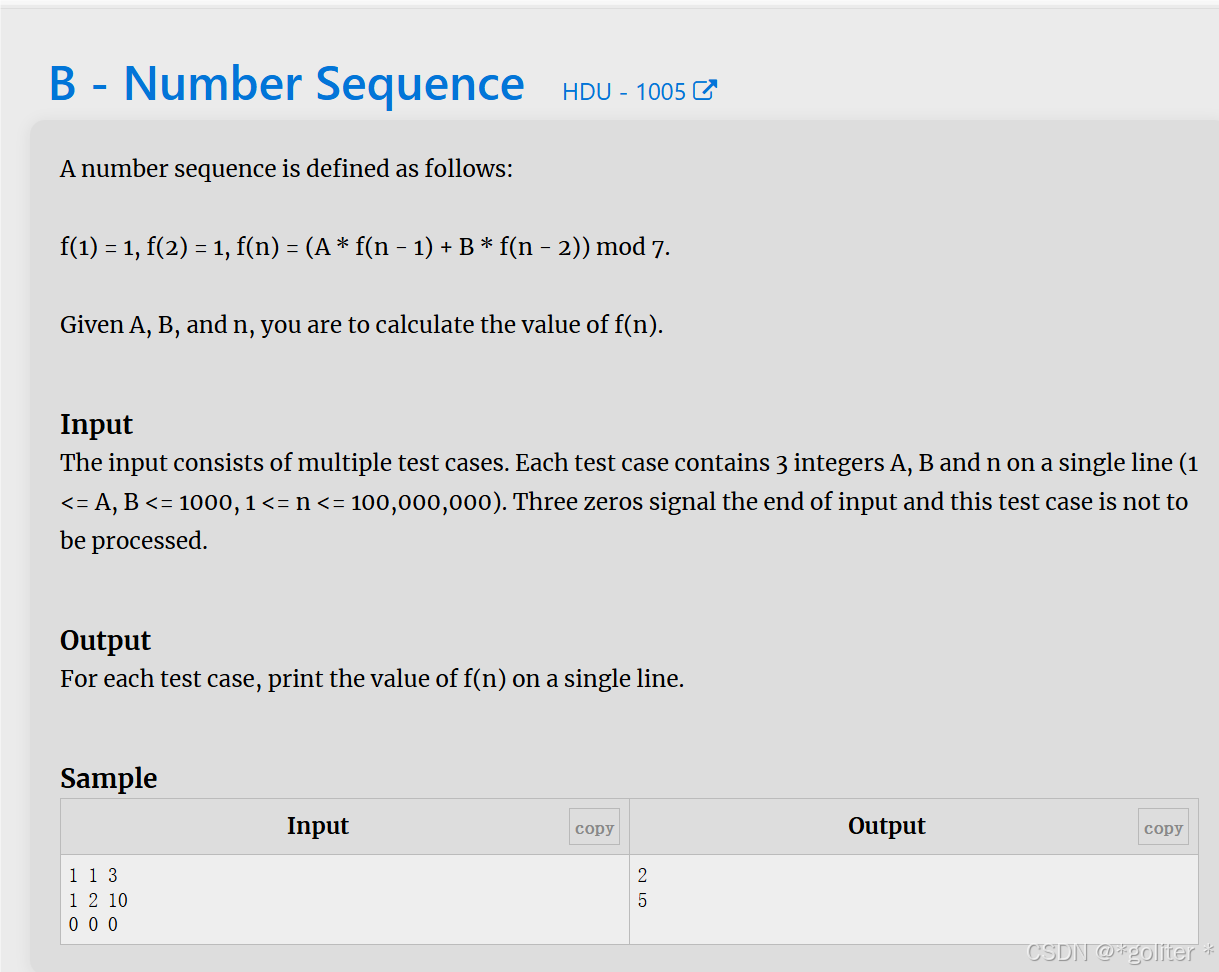
9、Number Sequence

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=7;
typedef struct{
	ll m[2][2];
}matrix;
matrix P={
	1,1,
	1,0
};
matrix I={
	1,0,
	0,1
};
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<2;i++){
		for(int j=0;j<2;j++){
			c.m[i][j]=0;
			for(int k=0;k<2;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}
int main(){
	ll a,b,n;
	while(cin>>a>>b>>n){
		if(a==0&&b==0&&n==0)break;
		P.m[0][0]=a;P.m[0][1]=b;
		ll sum=0;
		if(n==-1)break;
		if(n==0){
			cout<<0<<endl;
			continue;
		}
		if(n==1){
			cout<<1<<endl;
			continue;
		}
		matrix tmp=quickpow(n-2);
		sum=(tmp.m[0][0])%mod+(tmp.m[0][1])%mod;
		sum=(sum%mod+mod)%mod;
		cout<<sum<<endl;
	}
	return 0;
}

模板

10、Fibonacci

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mod=10000;
typedef struct{
	ll m[2][2];
}matrix;
matrix P={
	1,1,
	1,0
};
matrix I={
	1,0,
	0,1
};
matrix mul(matrix a,matrix b){
	matrix c;
	for(int i=0;i<2;i++){
		for(int j=0;j<2;j++){
			c.m[i][j]=0;
			for(int k=0;k<2;k++){
				a.m[i][k]=(a.m[i][k]%mod+mod)%mod; 
				b.m[k][j]=(b.m[k][j]%mod+mod)%mod; 
				c.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
			}
			c.m[i][j] = (c.m[i][j]%mod+mod)%mod;
		}
	}
	return c;
}
matrix quickpow(ll n){
	matrix m=P,b=I;
	while(n){
		if(n&1)b=mul(b,m);
		n>>=1;
		m=mul(m,m);
	}
	return b;
}
int main(){
	ll n;
	while(cin>>n){
		ll sum=0;
		if(n==-1)break;
		if(n==0){
			cout<<0<<endl;
			continue;
		}
		if(n==1){
			cout<<1<<endl;
			continue;
		}
		matrix tmp=quickpow(n-2);
		sum=(tmp.m[0][0])%mod+(tmp.m[0][1])%mod;
		sum=(sum%mod+mod)%mod;
		cout<<sum<<endl;
	}
	return 0;
}

求最后四位就是%10000

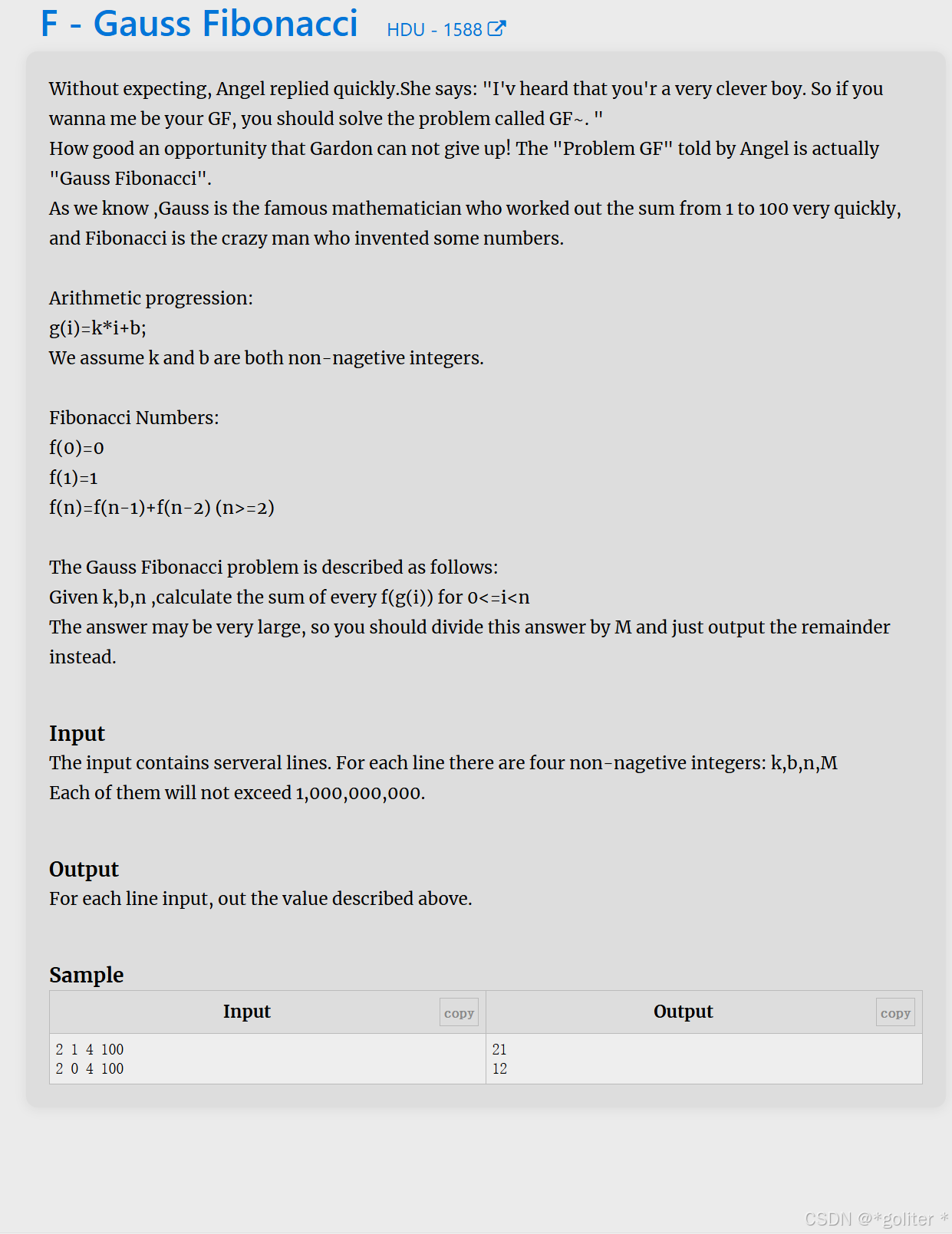
11、Gauss Fibonacci

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct matrie{
    ll m[10][10];
};
int k,b,n,mod;
matrie A,B,T,C,D,E;
matrie multi(matrie a,matrie b){
	matrie c;
	memset(c.m,0,sizeof(c.m));
	for(int i=0;i<10;i++){
		for(int j=0;j<10;j++){
			for(int k=0;k<10;k++){
				c.m[i][j]=(a.m[i][k]*b.m[k][j]+c.m[i][j])%mod;
			}
		}
	}
	return c;
}
matrie fast_power(matrie a, ll b) {
    matrie res;
    memset(res.m,0,sizeof(res.m));
    for(int i = 0; i < 10; ++i)res.m[i][i] = 1;
    while(b>0){
        if(b&1){
            res=multi(res,a);
        }
        b>>=1;
        a=multi(a, a);
    }
    return res;
}
void init(){
	T.m[0][0]=0;T.m[0][1]=1;T.m[1][0]=1;T.m[1][1]=1;
	A.m[0][0]=0;A.m[0][1]=1;
	C=multi(A,fast_power(T,b));
	E=fast_power(T,k);
	for(int i=0;i<2;i++){
		D.m[i][i]=1;
		B.m[i][i]=B.m[i][i+2]=1;
	}
	for(int i=2;i<4;i++){
		for(int j=0;j<2;j++){
			D.m[i][j]=D.m[i][j+2]=E.m[i-2][j];
		}
	}
}
int main(){
	while(scanf("%d%d%d%d",&k,&b,&n,&mod)!=EOF){
		init();
		matrie tmp=multi(B,fast_power(D,n-1));
		matrie sum;
		memset(sum.m, 0, sizeof(sum.m));
		for(int i=0;i<2;i++){
			for(int j=0;j<2;j++){
				sum.m[i][j]=tmp.m[i][j];
			}
		}
		matrie ans=multi(C,sum);
		printf("%lld\n", ans.m[0][0]);
	}
	return 0;
}

详解可以看看这篇博客HDU 1588 Gauss Fibonacci(分块矩阵优化)-CSDN博客

12、Fast Matrix Calculation

#include<bits/stdc++.h>
#define LL long long int 
const int MOD=6;
int n,m;
struct node{
    LL m[10][10];
    node()
    {
        memset(m,0,sizeof(m));
    }
};
int a[1005][10],b[10][1005],c[1005][10],d[1005][1005];
node cla(node A,node B)
{
    node C;
    for(int i=0;i<m;i++)//A对应的行 
        for(int j=0;j<m;j++)//B对应的列 
            for(int k=0;k<m;k++) 
            if(A.m[i][k]&&B.m[k][j])//剪枝（添条件，设门槛），提高效率，有一个是0，相乘肯定是0
            {
                C.m[i][j]+=A.m[i][k]*B.m[k][j];
                C.m[i][j]%=MOD;
            }
    return C;
}
node POW(int k,node ans)
{   
    node e;
    for(int i=0;i<m;i++) e.m[i][i]=1;
    while(k)
    {
        if(k%2) e=cla(e,ans);
        ans=cla(ans,ans);
        k/=2;
    }
    return e; 
} 
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==0&&m==0)
        break;
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        memset(c,0,sizeof(c));
        memset(d,0,sizeof(d));
        for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        scanf("%d",&a[i][j]);
        for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
        scanf("%d",&b[i][j]);
        node ans;
        for(int i=0;i<m;i++)//A对应的行 
        for(int j=0;j<m;j++)//B对应的列 
            for(int k=0;k<n;k++) 
            if(b[i][k]&&a[k][j])//剪枝（添条件，设门槛），提高效率，有一个是0，相乘肯定是0
            {
                ans.m[i][j]+=b[i][k]*a[k][j];
                ans.m[i][j]%=MOD;
            }
        ans=POW(n*n-1,ans);
        for(int i=0;i<n;i++)//A对应的行 
        for(int j=0;j<m;j++)//B对应的列 
            for(int k=0;k<m;k++) 
            if(a[i][k]&&ans.m[k][j])//剪枝（添条件，设门槛），提高效率，有一个是0，相乘肯定是0
            {
                c[i][j]+=a[i][k]*ans.m[k][j];
                c[i][j]%=MOD;
            }

        for(int i=0;i<n;i++)//A对应的行 
        for(int j=0;j<n;j++)//B对应的列 
            for(int k=0;k<m;k++) 
            if(c[i][k]&&b[k][j])//剪枝（添条件，设门槛），提高效率，有一个是0，相乘肯定是0
            {
                d[i][j]+=c[i][k]*b[k][j];
                d[i][j]%=MOD;
            }
        int sum=0;
        for(int i=0;i<n;i++)//A对应的行 
        for(int j=0;j<n;j++)//B对应的列 
        sum+=d[i][j];
        printf("%d\n",sum); 
    }
}

因为n实在太大了，开不了1000*1000的矩阵，但是可以利用矩阵相乘的结合律将（A*B）^n转换为A*(B*A)^(n-1)*B，这样B和A相乘得到的是一个6*6(最多)矩阵, 将这个矩阵用快速幂计算(n*n-1)次幂，在乘上一开始的A和最后的B即可。