2024-8-29,星期四,20:01,天气:晴,心情:晴。今天没什么事情发生,继续学习。
今天完成了第七章的学习,主要学习内容为:开环响应(频率响应+相移响应)+闭环响应(负反馈对带宽的影响+增益-带宽积)+正反馈与稳定性/补偿(选学)。
一、运算放大器响应(续)
1. 运算放大器开环响应
开环响应表示该运算放大器没有外部反馈;频率响应用以表明电压增益随频率变化的规律,相位响应表明输入信号与输出信号之间的相移随频率变化的规律。
(1)频率响应:从昨天的学习中我们可以知道,对于大多数运算放大器来说,大于截止频率时,一般假设运算放大器的下降率是常量(斜率是常数),即20dB / 十倍频,下降率为20dB / 十倍频的运算放大器称为补偿运算放大器,一个补偿运算放大器会有一个RC迟滞网络,用以确定其频率特性,因此,补偿运算放大器的下降率基本与RC网络相同。对于一些运算放大电路,情况比较复杂,频率响应由内部许多级的电路决定,每级电路都有自己的截止频率,总的频率响应受到内部多个级联电路的影响,这种放大器称为非补偿运算放大器,对于非补偿运算放大器需要特别注意反馈网络以避免震荡,如下图所示的三级运算放大器:
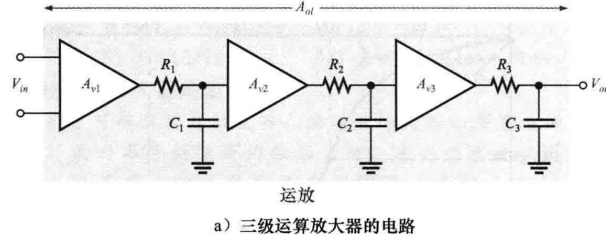
,每级的频率响应如下图所示:
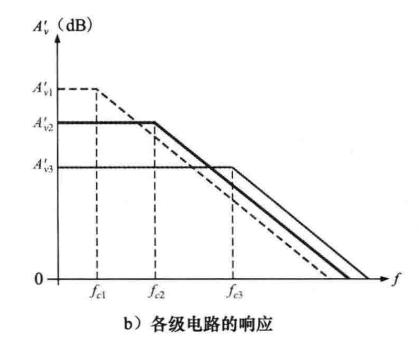
dB的增益是相加的(非对数相乘),于是运算放大器的总频率响应如下图所示:
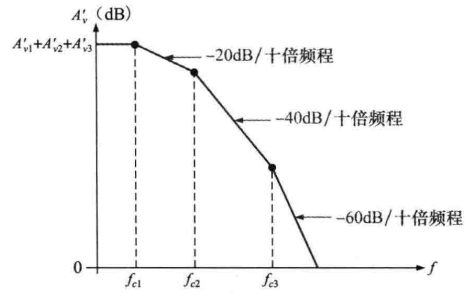
因为总的下降率是想加的,所以每到一个截止频率总的下降率就增加-20dB / 十倍频程。
(2)相移响应:在多级放大电路中,每级电路对总的相移都会有贡献,每个RC网络产生的相移最大为-90°,则一个三级放大器的相移滞后最大可达-270°,同样的,当频率小于截止频率时,相移小于45°;当频率等于截止频率时,相移等于45°;当频率大于截止频率时,相移大于45°。将每级运算放大器的相移滞后相加,得到的就是总的相移滞后,例如一的三级运算放大器的相移滞后如下:

2. 运算放大器的闭环响应
结合前面所学的知识我们可以知道,负反馈的加入会减小中频增益,对同相放大器Acl(NI) = (Rf / Ri) + 1;对于电压跟随器Acl(VF) ≈ 1;对于反相放大器Acl(I) ≈ -Rf / Ri。
(1)负反馈对带宽的影响:一个闭环运算放大器的截止频率为fc(cl) = fc(ol)(1 + BAol(mid))(该式的推导见注),从表达式可以看出,由于因子1 + BAol(mid),闭环截止频率fc(cl)要大于开环截止频率fc(ol),其中,B是反馈衰减因子,B = Ri / (Ri + Rf),因为fc(cl)等于闭环放大器的带宽,所以带宽同样随着相同的倍数增加,即BWcl = BWol(1 + BAol(mid)),例如下图所示:
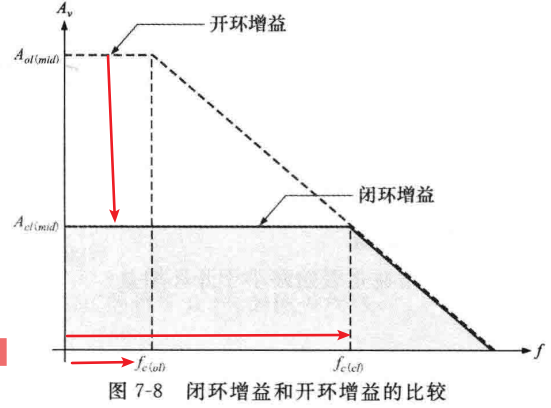
上图说明了闭环对增益的影响,当负反馈使开环增益减小时,带宽会增加,需要注意的是,闭环增益和开环增益是彼此独立的,超过闭环截止频率后,闭环增益和开环增益具有相同的下降率。
(2)增益-带宽积:由于增益和带宽的乘积是常量,所以闭环增益的增加会引起带宽的下降,反之亦然(前提是下降率是固定的-20dB / 十倍频程),令Acl表示任意闭环增益,fc(cl)为闭环截止频率(带宽),则Aclfc(cl) = Aolfc(ol),增益-带宽始终等于运算放大器的单位增益带宽,即Aclfc(cl) = 单位-增益带宽。
注:

2. 正反馈和稳定性(选学)
通过前面的学习我们可以知道,稳定性对运算放大器来说是非常重要的,稳定运行是指运算放大器在任何情况下都不会振荡,当输入端没有信号时,由于输入端的噪声和瞬态电压,输出端会有不期望的电压波动。
(1)正反馈:通过负反馈,反馈到输入端的信号与输入信号相位相差180°,反馈信号与输入信号相抵,因此减去反馈信号可以有效地减小电压增益,所以只要反馈信号是负的,放大器就是稳定的,当从输出端反馈到输入端的信号的相位与输入信号一致时(相移为0°),正反馈条件成立,放大器会发生振荡。
(2)环路增益:闭环放大器的环路增益定义为运算放大器的开环增益乘以反馈网络的衰减因子,即环路增益 = AolB。要产生不稳定,运放电路需要满足两个条件:(a)必须要有正反馈;(b)闭环放大器的环路增益必须大于1。
(3)相位裕量:对于负反馈运算放大器电路,由于反馈环接到反相输入端,所以输入与输出端存在180°的固有相移,此外,放大器中的RC滞后网络会产生附加的相移φtot,因此反馈环总相移为180°+φtot。相位裕量φpm是使得反馈环的总相移为360°时的额外相移,180° + φtot +φpm = 360°,则φpm = 180° - |φtot|,如果相位裕量是负的,则总相移小于360°,放大器是稳定的;如果相位裕量是0或负值则表明反馈信号是以输入信号同相反馈的,放大器存在潜在的不稳定风险,从上式可以看出,当总的滞后网络相移(φtot)等于或超过180°时,存在不稳定状态。
(4)稳定性分析:当运算放大器的下降率超过-20dB/十倍频程时,对于电路稳定性有以下结论:放大器的闭环增益必须要与开环增益在-20dB/十倍频程的线段上相交,才能保证中频范围内所有频率处的稳定性;如果闭环增益与开环增益在-40dB/十倍频程的位置相交的话,就会发生临界稳定或完全不稳定;如果闭环增益与开环增益在-60dB/十倍频程上相交,则一定会发生不稳定(使用特殊设计的放大器除外),因此工作时运算放大器的闭环增益必须使得从主截止频率处开始得下降率不超过-20dB/十倍频程。
3. 运算放大器的补偿(选学)
在上面的学习中,我们知道,当运算放大器的下降率超过-20dB/十倍频程,并且运算放大器得闭环增益曲线与开环响应相交于更高得下降率时,就会出限不稳定,这样得话闭环电压增益势必要被限制在很高的值,但是在很多应用中,低电压增益是非常有必要的,所以,为了保证稳定性,必须要进行相位滞后补偿。
(1)相位滞后补偿:放大器不稳定的原因是运算放大器内部滞后网络的额外相移,当相移超过180°时,放大器就会振荡,这时有两种方法:一是通过补偿的方法来去除开环下降率大于-20dB/十倍频程的部分,二是通过补偿将-20dB/十倍频程下降的曲线延伸到更低的频率。
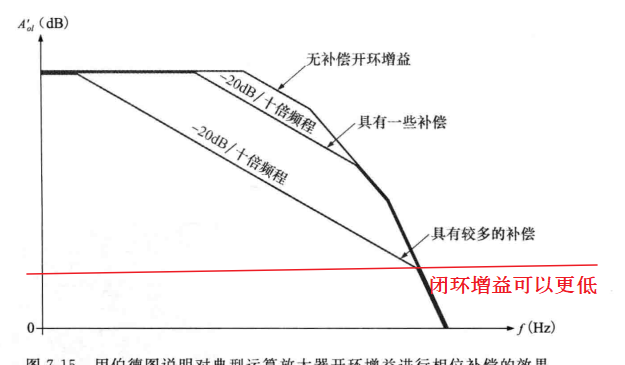
(2)补偿网络:集成电路运算放大器的补偿方式分为内部补偿和外部补偿两种,两种方法均需要加入RC网络,如下图所示:
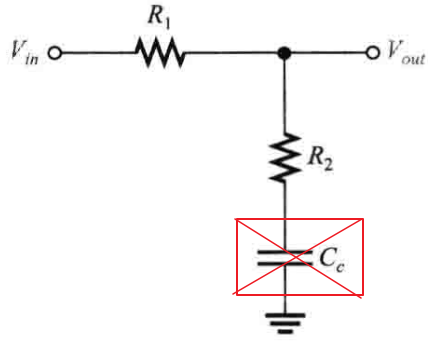
当工作在低频处时,补偿电容的电抗XCc非常大,相当于开路,输出电压几乎等于输入电压,当频率达到截止频率时,fc = 1 / [2Π(R1 + R2Cc)],输出电压按20dB/十倍频程下降,该下降频率会一致持续到XCc ≈ 0,在XCc ≈ 0时,输出电压由R1和R2决定(补偿电容相当于导线),如下图所示:
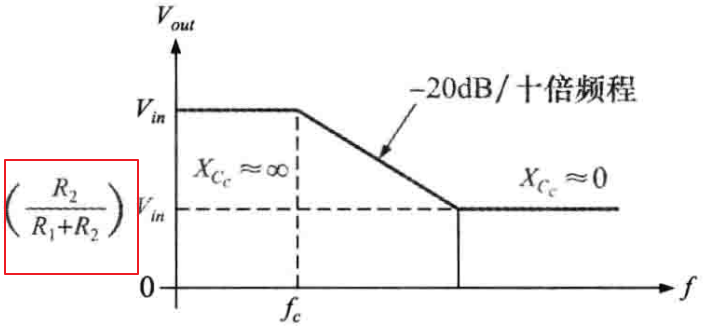
(3)补偿范围:较大的补偿电容会使开环响应从叫低的频率处就开始下降,因此会使-20dB/十倍频程的下降延伸到较低的增益值,如下图所示
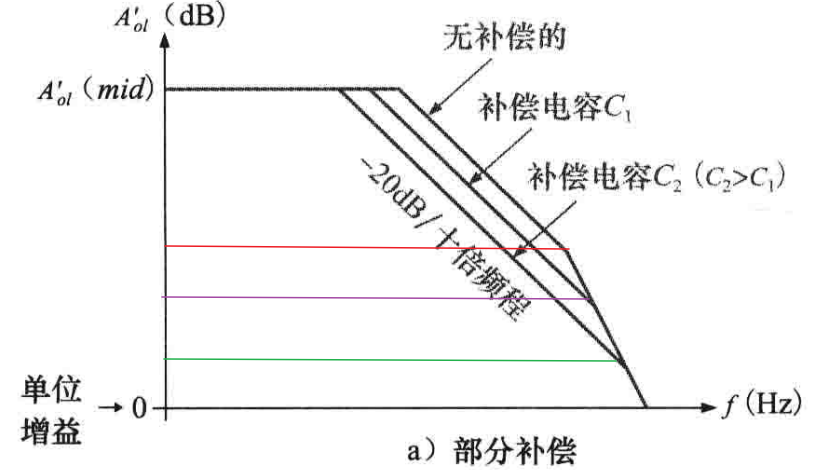
因此,通过足够大的补补偿电容可以使运算放大器无条件的稳定,如下图所示:
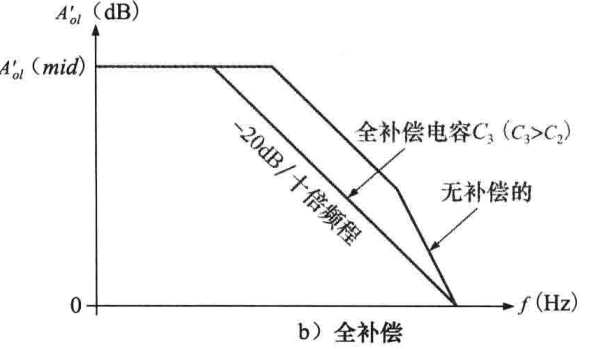
上图的-20dB/十倍频程一直延伸到单位增益,称为内部全补偿运算放大器,可以用于任何值得闭环增益并保持稳定。内部全补偿的缺点是牺牲了带宽,降低了转换效率,所以一般集成电路上会使用外部补偿,通过预留一个特定的引脚连接外部补偿电容实现。