前言
之前的文章中多任务学习MTL模型:MMoE、PLE,介绍了针对多任务学习的几种模型,着重网络结构方面的优化,减缓task之间相关性低导致梯度冲突,模型效果差,以及task之间的“跷跷板”问题。
但其实多任务学习还存在另外一些棘手的问题:
1、不同task的loss量级不同,可能会出现loss较大的task主导的现象(loss较大的task,梯度也会较大,导致模型的优化方向很大程度上由该task决定);
2、不同task的学习速度不同,有的慢有的快;
3、不同的loss应该分配怎样的权重?直接平均?如何选出最优的loss权重组合?
Using Uncertainty to Weigh Losses
相关论文:《Multi-Task Learning Using Uncertainty to Weigh Losses for Scene
Geometry and Semantics》
这篇论文指出了多任务学习模型的效果很大程度上由共享的权重决定,但训练这些权重是很困难。由此引出uncertainty的概念,来衡量不同的task的loss,使得可以同时学习不同类型的task。
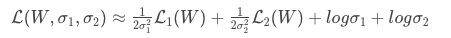
-
其中, α {\alpha} α为可学习参数,论文认为它是对应task建模的uncertainty(不确定性)。
-
容易看出,总的loss会惩罚loss大且 α {\alpha} α小的task,因为对于这种task, 1 2 α 2 L {\frac{1}{2\alpha^2}L} 2α21L这一项就会很大,SGD就会将它往小优化;
-
它代表着对于loss较大的task,意味着它的uncertainty(不确定性)也较高,为了避免模型往错误的方向“大步迈”,应该以较小的梯度去更新w;相反的,对于loss较小的task,它的uncertainty也就较低,以较大的梯度去更新w;
-
同时,这也能避免让较大loss的task主导的问题。
总结:大loss的task给予小权重,小loss的task给予大权重。
注意事项:这个方法由于后面的log项,可能会出现总loss为负的情况。
GradNorm
相关论文:《GradNorm: Gradient Normalization for Adaptive Loss Balancing in
Deep Multitask Networks》
这篇论文提出一个新的方法:梯度正则化gradient normalization (GradNorm),它能自动平衡多task不同的梯度量级,提升多任务学习的效果,减少过拟合。
首先,总loss的定义仍是不同task的loss加权平均:
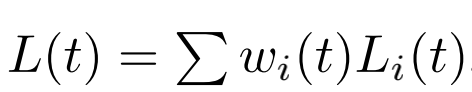
GradNorm设计了额外的loss来学习不同task loss的权重 w i {w_i} wi,但它不参与网络层的参数的反向梯度更新,目的在于不同task的梯度通过正则化能够变成同样的量级,使不同task可以以接近的速度进行训练:
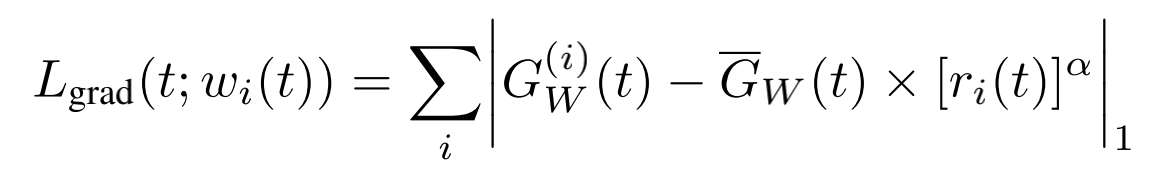
其中,t代表训练的步数;
W一般是取最后一层共享网络层shared layer的权重;
第i个task的正则化梯度,即loss对W的梯度,然后再做L2-norm:
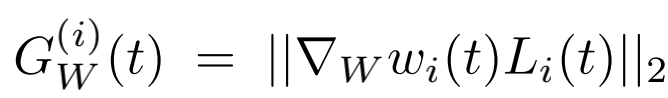
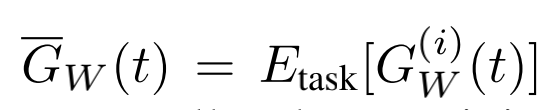
第i个task的loss(第t步)与初设loss比率,用来代表学习速度:

第i个task的相对学习速度:
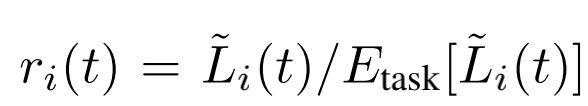
注意事项:
1、容易看出不同task的初设loss: L i ( 0 ) {L_i(0)} Li(0),对学习速度的计算影响很大。
如果所有网络层有着稳定的参数初设化,则可以直接使用(第一次的loss);
但如果 L i ( 0 ) {L_i(0)} Li(0)对参数初设化方式很敏感,在多分类中,则可以令 L i ( 0 ) = l o g ( C ) {L_i(0)}=log(C) Li(0)=log(C),C为分类数。
2、论文的流程是在每轮训练中,先通过反向传播进行不同task loss的权重 w i {w_i} wi,再进行网络参数的更新。
Dynamic Weight Average
相关论文:《End-to-End Multi-Task Learning with Attention》
这篇论文仍然致力于寻找平衡多个task训练的方法,提出了一种**Dynamic Weight Average (DWA)**的方法,它比较简单直接,与GradNorm不同,不需要计算梯度,而是只需要task的loss。
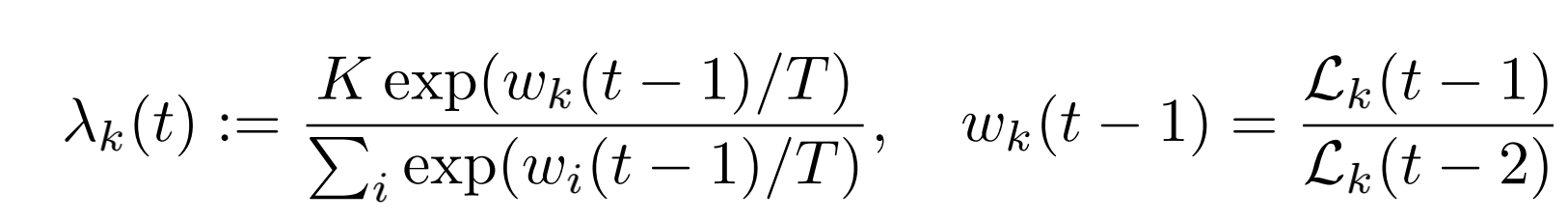
- λ k {\lambda_k} λk为task的权重,即总的loss仍为所有task的loss加权平均: L t o t a l = ∑ k λ k L k {L_{total}=\sum_k\lambda_kL_k} Ltotal=∑kλkLk
- w_k则为上一轮以及上上轮的loss比率,代表不同task的学习速率
- T起到平滑task权重的作用,T越大,不同task的权重分布越均匀。甚至T足够大的话,则 λ k ≈ 1 {\lambda_k} \approx 1 λk≈1,每个task的权重相等
- K则是让所有task的权重加权求和后为K: ∑ k λ k = K {\sum_k\lambda_k=K} ∑kλk=K。因为一般情况下不特殊处理的话,每个task的权重都相等为1,那么所有task加权之后便为K。
Pareto-Eficient
相关论文:《A Pareto-Efficient Algorithm for Multiple Objective Optimization
in E-Commerce Recommendation》
这篇论文对总loss的定义仍然是所有task的loss加权平均,但这个权重是经过正则化(scalarization)的:
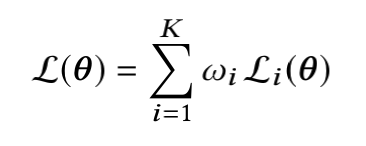
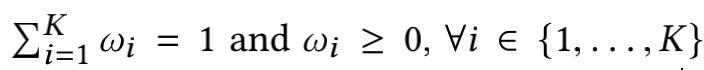
不过,论文指出了不同task会有不同的优先级,比如一个task为点击预测,一个task转化预测,那肯定转化预测的task的优先级更高,因此,可以为不同task的权重增加了一个边界条件:
w i ≥ c i , 0 < c i < 1 , ∑ K c i ≤ 1 {w_i \ge c_i},\ 0<c_i<1,\ \sum_Kc_i \le 1 wi≥ci, 0<ci<1, ∑Kci≤1
我们的目标当然是让总loss即 L ( θ ) {L(\theta)} L(θ)最小,常规做法,对 L ( θ ) {L(\theta)} L(θ)求导,然后令其导数等于0,即为下式:
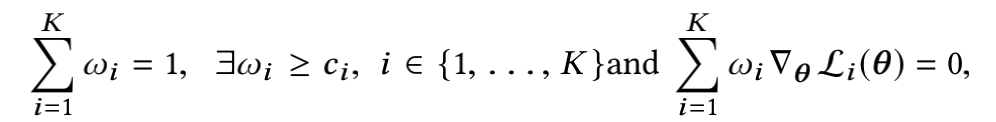
满足这种条件的解法称为Pareto stationary(帕累托平稳)
以上式子可以转化为:(K个 w i ▽ θ L i ( θ ) {w_i\triangledown_\theta L_i(\theta)} wi▽θLi(θ) 二范数之和的最小值即为0,最小化就是在往0逼近)
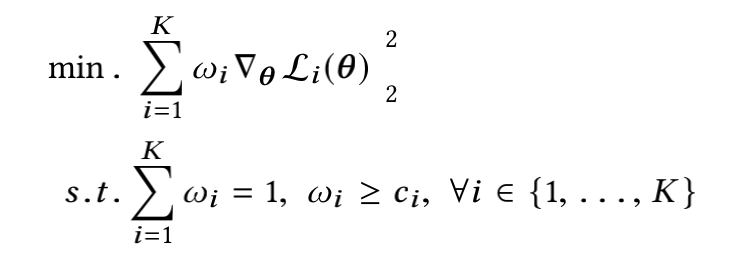
论文也给出了最优的task的权重组合解法:
令 w ^ i = w i − c i {\hat{w}_i = w_i - c_i} w^i=wi−ci,则不等式变成:
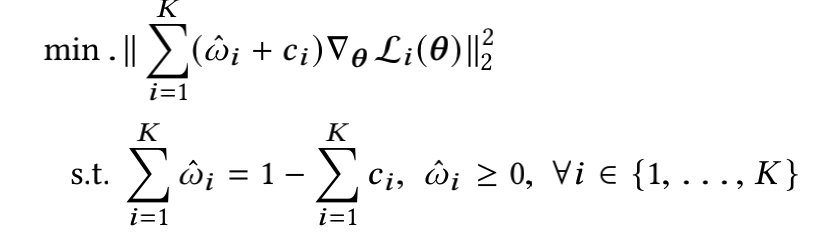
然后根据以上理论求出 w ^ {\hat{w}} w^的所有解 w ^ ∗ {\hat{w}}^* w^∗,但是可能会出现负数的解。
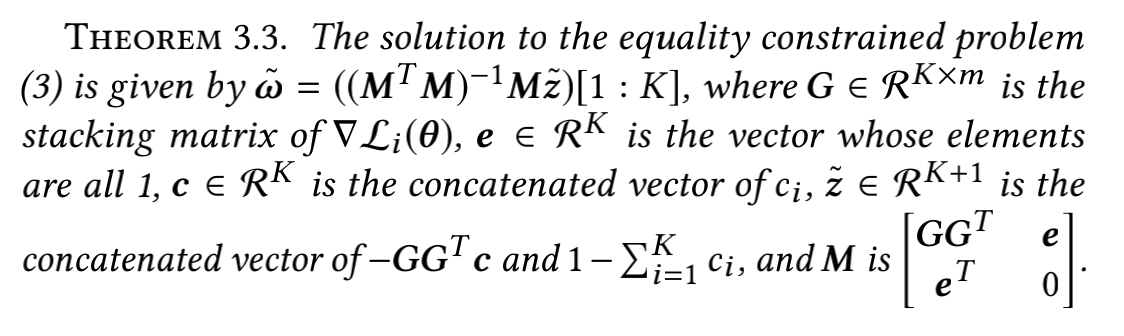
由于上述求出的 w ^ ∗ {\hat{w}}^* w^∗可能为负,并且为了能够用上的解,最终转化为非负的最小二乘问题:
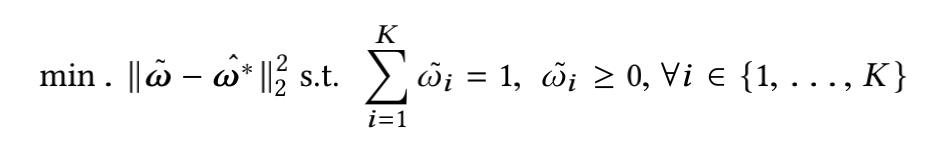
总结
以上论文都是为了解决不同task的loss量级或者学习速度不同,求出最优的task权重组合;
大致流程都相同:先对模型参数进行反向传播进行更新,再使用各自的算法更新task权重。
-------------------------------------------------------- END --------------------------------------------------------
以上的算法实现:github