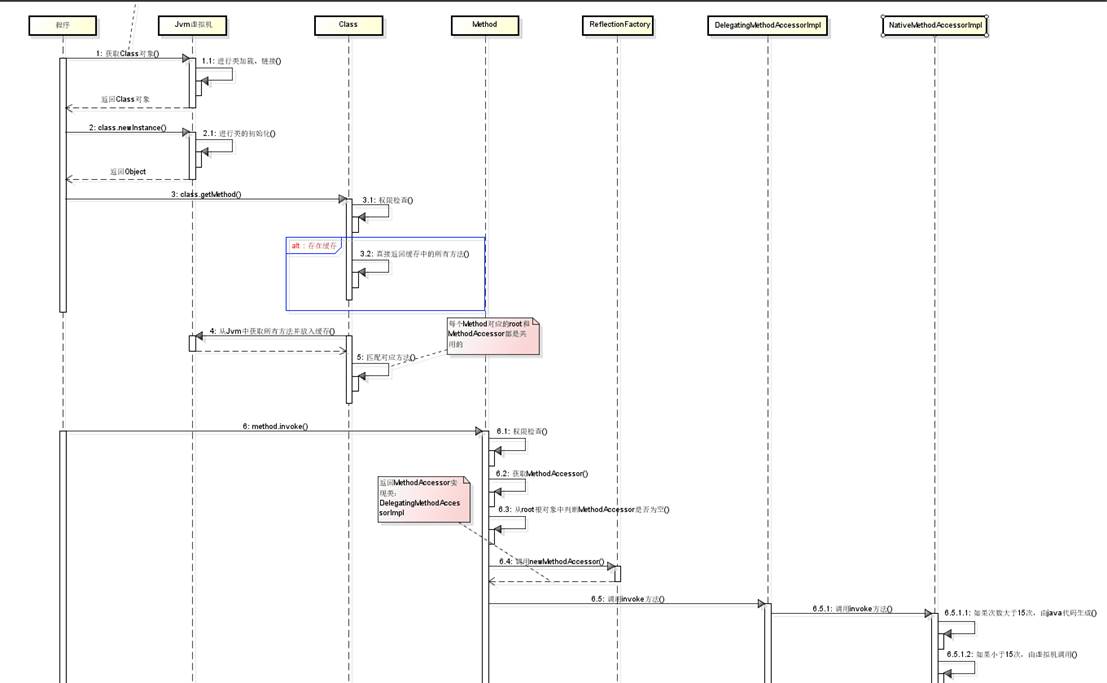
独立分量分析 ICA
等度量映射 ISOMAP
线性判别分析 LDA
(拉普拉斯)数据降维方法 LE
局部线性嵌入 LLE
多维尺度变换MDS
主成分分析 PCA
核主成分分析 KPCA
稀疏主成分分析SPCA
奇异值分解SVD
特征矩阵的联合近似对角化 JADE

降维目的:克服维数灾难,获取本质特征,节省存储空间,去除无用数据,实现数据可视化。
目前很多实验所需要的数据均为高维数据,也就是多列变量值决定目标值。高维数据有一定的优点,数据维度高,则其所包含的信息量就大,则可供决策的依据就较多。但是数据不是维度越高越好,因为还需要考虑实际的计算能力,高维度数据的缺点,消耗计算资源,计算时间大,同时使得冗余且耦合的数据对实验结果造成影响,甚至造成“维度灾难”。所以为了适应需要,获取数据的本质特征,降维算法随之诞生。以下是对提到的各种数据分析方法的简要分析:
- 独立分量分析 (ICA)
独立分量分析是一种计算方法,用于从多元统计数据中找到隐藏的因子或成分,这些因子或成分在统计上是尽可能独立的。ICA在信号处理、神经科学和盲源分离等领域有广泛应用。
- 等度量映射 (ISOMAP)
等度量映射是一种非线性降维技术,它试图保持数据点之间的测地距离(即两点之间的最短路径距离)。ISOMAP特别适用于发现嵌入在高维空间中的低维流形结构。
- 线性判别分析 (LDA)
线性判别分析是一种监督学习方法,用于分类和降维。它通过找到一个投影方向,使得同类之间的投影点尽可能接近,而不同类之间的投影点尽可能远离。
- (拉普拉斯)数据降维方法 (LE)
拉普拉斯特征映射(Laplacian Eigenmaps,简称LE)是一种基于图的非线性降维技术。它构建了一个表示数据点之间相似性的图,并试图保持数据点之间的局部邻接关系。
- 局部线性嵌入 (LLE)
局部线性嵌入是一种无监督的非线性降维方法。它假设数据点可以由其局部邻域的线性组合近似,并试图在降维后的空间中保持这种局部线性关系。
- 多维尺度变换 (MDS)
多维尺度变换是一种统计技术,用于将高维空间中的对象(如观测值或变量)映射到低维空间,同时尽可能保留对象之间的相似性。
- 主成分分析 (PCA)
主成分分析是一种广泛使用的线性降维技术。它通过正交变换将原始特征转换为一组线性不相关的新特征,称为主成分,这些主成分按照方差大小排序。
- 核主成分分析 (KPCA)
核主成分分析是PCA的非线性扩展,它通过使用核函数将数据映射到高维特征空间,然后在这个空间中执行PCA。这使得KPCA能够发现数据中的非线性结构。
- 稀疏主成分分析 (SPCA)
稀疏主成分分析是PCA的一个变种,它试图找到的主成分在原始特征上具有稀疏性,即大部分系数为零。这有助于解释性和可解释性。
- 奇异值分解 (SVD)
奇异值分解是一种在线性代数中常用的方法,它可以对矩阵进行分解,类似于PCA中的协方差矩阵分解。SVD在信号处理、图像处理等领域有广泛应用。
- 特征矩阵的联合近似对角化 (JADE)
特征矩阵的联合近似对角化是一种用于盲源分离的技术,特别是用于独立分量分析。它试图通过联合对角化多个特征矩阵来找到一组独立的源信号。
这些技术各自具有不同的特点和适用场景,选择哪种方法取决于数据的性质、问题的需求以及计算资源的限制。
%加载数据,数据为480*8的矩阵,总共12类,每类40*8,这是对12类进行聚类
clc
clear
load('data.mat')
addpath('Fun')
%% 进行二维可视化,需要生长与数据相对应的标签
mm=40; % mm为每类样本数
lable=[ones(mm,1); 2*ones(mm,1); 3*ones(mm,1); 4*ones(mm,1);...
5*ones(mm,1); 6*ones(mm,1); 7*ones(mm,1); 8*ones(mm,1);...
9*ones(mm,1); 10*ones(mm,1); 11*ones(mm,1); 12*ones(mm,1)];
%% 利用降维方法对数据进行降维处理,二维可视化,就降到2维,三维可视化,就降到3维
k=3; %最近邻数,这个参数影响聚类效果
d=3;% 最终降到的维度,2
lambda = 1; % 正则化系数
data2DLLE = LLE(data, k, d); %生成2D降维数据
data2Dtran = LE(data, k , d);
% [U,D,V]=MySVD(data);
[alpha, w, err] = spca(data, d, lambda);
eig_vec_selected=PCA(data',d);
reduced_features=LDA(data,lable);
data_kpca=KPCA(data,d);
[A,S]=jade(data,d);
%MDSMat = MyMDS(data', d);%data需要方阵
% Z = isomap(data', k, d);%data需要方阵
%ZZ = MDS(data, d); %data需要方阵