基于MATLAB的涡流函数方法案例+代码

news2024/9/20 1:04:24

前言

这里介绍一下相关理论和代码----基于MATLAB使用伪谱离散化 + 三阶龙格库塔时间积分实现涡流函数方法的CFD案例

1. 代码详解

这段 MATLAB 代码实现了一个二维湍流模拟，使用伪谱法在周期性边界条件下解算非线性涡度-流函数方程：

M = 256; % number of points
N = M;
Lx = 2*pi;
Ly = 2*pi;
nu = 5e-4; % kinematic viscosity
Sc = 0.7; % Schmidt number
beta = 0; % meridional gradient of Coriolis parameter
ar = 0.02; %random number amplitude
b = 1; % mean scalar gradient
CFLmax = 0.8;
tend = 200; % end time

x=linspace(0,Lx,M+1); x(end)=[];
dx = Lx/M;
kx=[0:M/2 -M/2+1:-1]*2*pi/Lx;

y=linspace(0,Ly,N+1); y(end)=[];
ky=[0:N/2 -N/2+1:-1]*2*pi/Ly;
dy = Ly/N;

time = 0;

index_kmax = ceil(M/3);
kmax = kx(index_kmax);
filter = ones(M,N);
filter(index_kmax+1:2*index_kmax+3,index_kmax+1:2*index_kmax+3)=0;

rng(64);
[u, v, omega, psi, ddx, ddy, idel2, kk, k2]=deal(zeros(M,N));

for j=1:N
    ddx(:,j)=1i*kx;
end

for i=1:M
    ddy(i,:)=1i*ky;
end

for i=1:M
    for j=1:N
        idel2(i,j)=-kx(i)^2-ky(j)^2;
    end
end
idel2=1./idel2;
idel2(1,1)=0;
for i=1:M
    for j=1:N
        kk(i,j)=kx(i)^2+ky(j)^2;
        k2(i,j)=kx(i)^2+ky(j)^2;

        if kk(i,j) >= 6^2 && kk(i,j) <= 7^2 % forcing
            kk(i,j) = -kk(i,j);
        end
        if kk(i,j) <= 2^2
            kk(i,j) = 8*kk(i,j); % large-scale dissipation
        end
    end
end
for i=1:M
    for j=1:N
        u(i,j) =  cos(2*x(i))*sin(2*y(j))+ar*rand;
        v(i,j) = -sin(2*x(i))*cos(2*y(j))+ar*rand;
    end
end
uhat = fft2(u);
vhat = fft2(v);
omegahat = ddx.*vhat - ddy.*uhat; % make vorticity
phi = rand(size(u));
phihat = fft2(phi);
dt = 0.5*min([dx dy]);
nstep = 1;
s2 = pcolor(x,y,phi'); 
title('Scalar');  
shading flat; 
axis equal tight; 
drawnow
while time < tend
    psihat = -idel2.*omegahat;
    uhat = ddy.*psihat;
    vhat = -ddx.*psihat;
    u = real(ifft2(uhat));

    v = real(ifft2(vhat));
    omegadx = real(ifft2(ddx.*omegahat));
    omegady = real(ifft2(ddy.*omegahat));
    facto = exp(-nu*8/15*dt*kk);
    factp = exp(-nu/Sc*8/15*dt*k2);
    r0o = -fft2(u.*omegadx+v.*omegady)+beta*vhat;

    r0p = -fft2(u.*real(ifft2(ddx.*phihat))+v.*real(ifft2(ddy.*phihat)))+b*vhat;
    omegahat = facto.*(omegahat + dt*8/15*r0o); % update omega
    phihat = factp.*(phihat + dt*8/15*r0p); % update phi

    %%%% Substep 2
    psihat = -idel2.*omegahat;

    uhat = ddy.*psihat;

    vhat = -ddx.*psihat;
    u = real(ifft2(uhat));

    v = real(ifft2(vhat));
    omegadx = real(ifft2(ddx.*omegahat));
    omegady = real(ifft2(ddy.*omegahat));
    r1o = -fft2(u.*omegadx+v.*omegady)+beta*vhat;
    r1p = -fft2(u.*real(ifft2(ddx.*phihat))+v.*real(ifft2(ddy.*phihat)))+b*vhat;
    omegahat = omegahat + dt*(-17/60*facto.*r0o + 5/12*r1o);
    phihat = phihat + dt*(-17/60*factp.*r0p + 5/12*r1p);
    facto = exp(-nu*(-17/60+5/12)*dt*kk);
    factp = exp(-nu/Sc*(-17/60+5/12)*dt*k2);
    omegahat = omegahat.*facto;
    phihat = phihat.*factp;
    %%%% Substep 3
    psihat = -idel2.*omegahat;
    uhat = ddy.*psihat;
    vhat = -ddx.*psihat;
    % max(max(abs(real(ifft2(1i*ddx.*uhat+1i*ddy.*vhat))))) % divergence
    u = real(ifft2(uhat));
    v = real(ifft2(vhat));
    omegadx = real(ifft2(ddx.*omegahat));
    omegady = real(ifft2(ddy.*omegahat));

    r2o = -fft2(u.*omegadx+v.*omegady)+beta*vhat;
    r2p = -fft2(u.*real(ifft2(ddx.*phihat))+v.*real(ifft2(ddy.*phihat)))+b*vhat;
    omegahat = omegahat + dt*(-5/12*facto.*r1o + 3/4*r2o);
    phihat = phihat + dt*(-5/12*factp.*r1p + 3/4*r2p);
    facto = exp(-nu*(-5/12+3/4)*dt*kk);
    factp = exp(-nu/Sc*(-5/12+3/4)*dt*kk);
    omegahat = omegahat.*facto;
    phihat = phihat.*factp;
    phihat = filter.*phihat;
    omegahat = filter.*omegahat;
    time = time + dt;
    nstep = nstep + 1;
    CFL = max(max(abs(u)))/dx*dt+max(max(abs(v)))/dy*dt;
    if mod(nstep,20)==0
        phi = real(ifft2(phihat));
        omega = real(ifft2(omegahat));
        dissipation = 2*nu*(real(ifft2(ddx.*uhat)).^2 + real(ifft2(ddy.*uhat)).^2 + real(ifft2(ddx.*vhat)).^2 + real(ifft2(ddy.*vhat)).^2);
        eta = (nu^3/mean(dissipation,'all'))^0.25;
        s2.CData = phi';
        drawnow
        fprintf(1,'step = %d    time = %g    dt = %g  CFL = %g    kmax*eta = %g %g\n', nstep, time, dt, CFL, eta.*kmax, eta.*kmax/sqrt(Sc));
    end
    dt = CFLmax/CFL*dt; %0.0005;
end

图片

1.1初始化参数

M = 256; % 网格点数（沿x方向）
N = M; % 网格点数（沿y方向）
Lx = 2*pi; % x方向的域长度
Ly = 2*pi; % y方向的域长度
nu = 5e-4; % 运动粘度
Sc = 0.7; % 施密特数（分子扩散率与动量扩散率的比值）
beta = 0; % 科里奥利系数
ar = 0.02; % 随机数幅度
b = 1; % 标量梯度的均值
CFLmax = 0.8; % 最大CFL数
tend = 200; % 结束时间

其中：

  • M 和 N 分别是 x 和 y 方向的网格点数。

  • Lx 和 Ly 是计算域的长度。

  • Sc 是施密特数，用于模拟标量的扩散。

  • ar 是用于初始化速度场的随机扰动的幅度。

  • b 是标量梯度的均值，用于定义标量场的强度。

1.2 网格与频率

x = linspace(0,Lx,M+1); x(end)=[];
dx = Lx/M;
kx=[0:M/2 -M/2+1:-1]*2*pi/Lx;

y = linspace(0,Ly,N+1); y(end)=[];
ky=[0:N/2 -N/2+1:-1]*2*pi/Ly;
dy = Ly/N;

  • x 和 y 是物理空间中的网格点。

  • kx 和 ky 是对应的频率空间中的波数向量。它们用于傅里叶变换后的计算。

1.3 时间循环的初始化

time = 0;
index_kmax = ceil(M/3);
kmax = kx(index_kmax);
filter = ones(M,N);
filter(index_kmax+1:2*index_kmax+3,index_kmax+1:2*index_kmax+3)=0;

rng(64);
[u, v, omega, psi, ddx, ddy, idel2, kk, k2] = deal(zeros(M,N));

  • time 初始化为 0。

  • index_kmax和kmax用于确定最大有效波数。

  • filter 是滤波器，用于在频率空间中滤除高频噪声。

  • u, v, omega, psi 等变量初始化为零矩阵。

1.4 初始化导数和拉普拉斯算子

for j=1:N
    ddx(:,j) = 1i*kx;
end

for i=1:M
    ddy(i,:) = 1i*ky;
end

for i=1:M
    for j=1:N
        idel2(i,j) = -kx(i)^2 - ky(j)^2;
    end
end
idel2 = 1./idel2;
idel2(1,1) = 0;

  • ddx 和 ddy 分别是 x 和 y 方向的微分算子，使用频率空间中的傅里叶变换定义。

  • idel2 是拉普拉斯算子的逆，用于求解流函数， idel2(1,1)=0 是为了避免数值发散。

1.5 初始条件

for i=1:M
    for j=1:N
        kk(i,j) = kx(i)^2 + ky(j)^2;
        k2(i,j) = kx(i)^2 + ky(j)^2;

        if kk(i,j) >= 6^2 && kk(i,j) <= 7^2 % 强制项
            kk(i,j) = -kk(i,j);
        end
        if kk(i,j) <= 2^2
            kk(i,j) = 8*kk(i,j); % 大尺度耗散
        end
    end
end

  • kk 和 k2 是频率空间中的波数平方，用于计算非线性项。

  • 对应不同的波数范围，对 kk 进行调整，用于引入大尺度耗散和强制项。

1.6 初始化速度场与标量场

for i=1:M
    for j=1:N
        u(i,j) = cos(2*x(i)) * sin(2*y(j)) + ar*rand;
        v(i,j) = -sin(2*x(i)) * cos(2*y(j)) + ar*rand;
    end
end

  • u 和 v 是速度场的初始条件，由一个基态流（cos-sin 形式）和小幅度随机扰动组成。

1.7 时间推进循环

主循环依次计算涡度、流函数、速度场和标量场的时间推进。每个时间步分为三部分（子步骤），并且使用了一种三阶 Runge-Kutta 时间积分方法。每一步中，代码会更新各个场量并应用滤波器以防止数值发散。

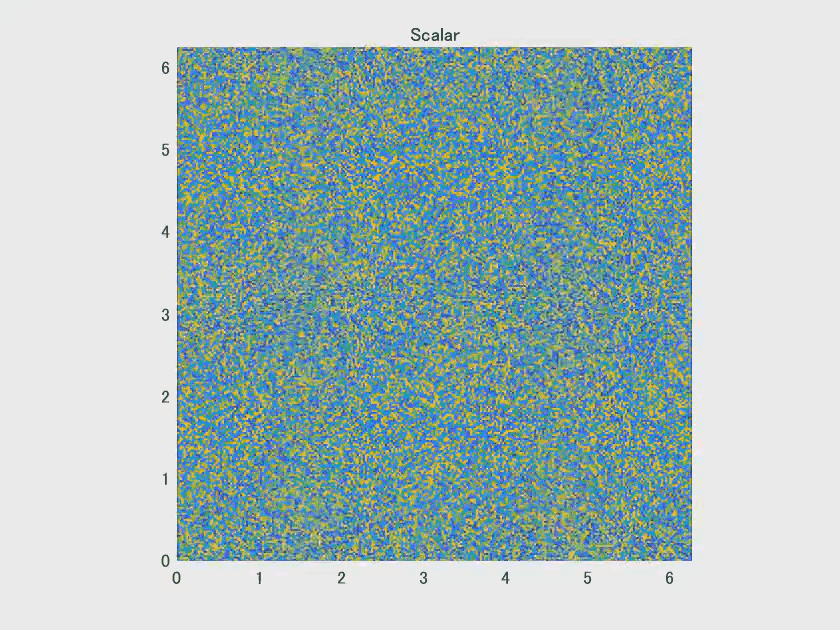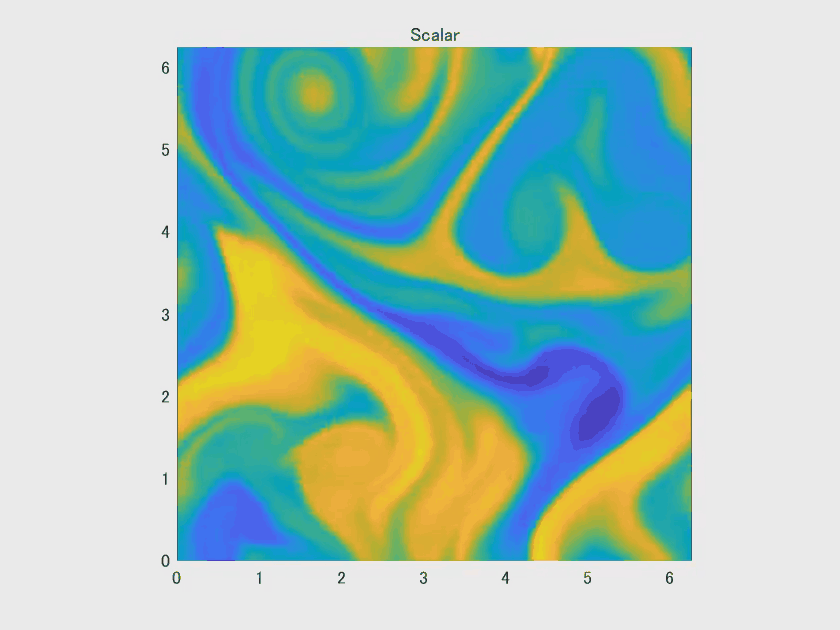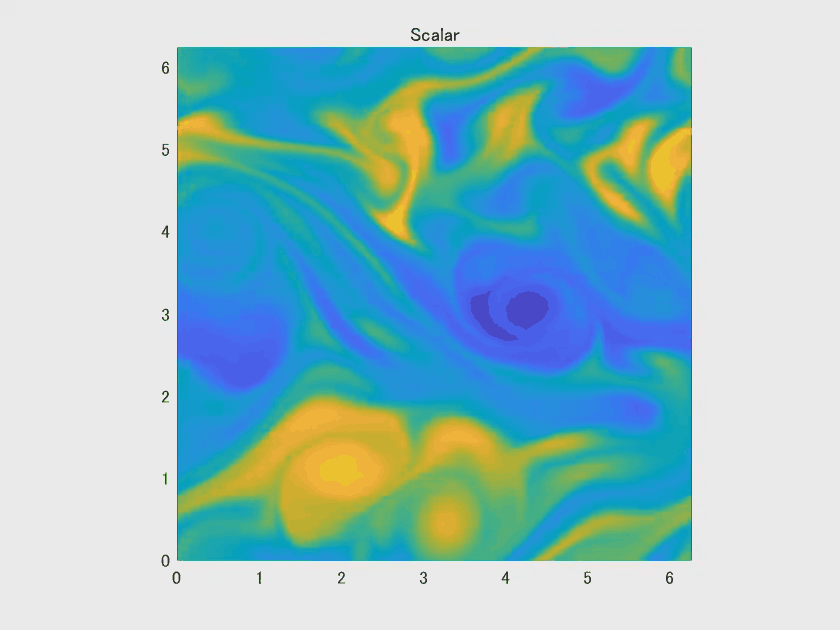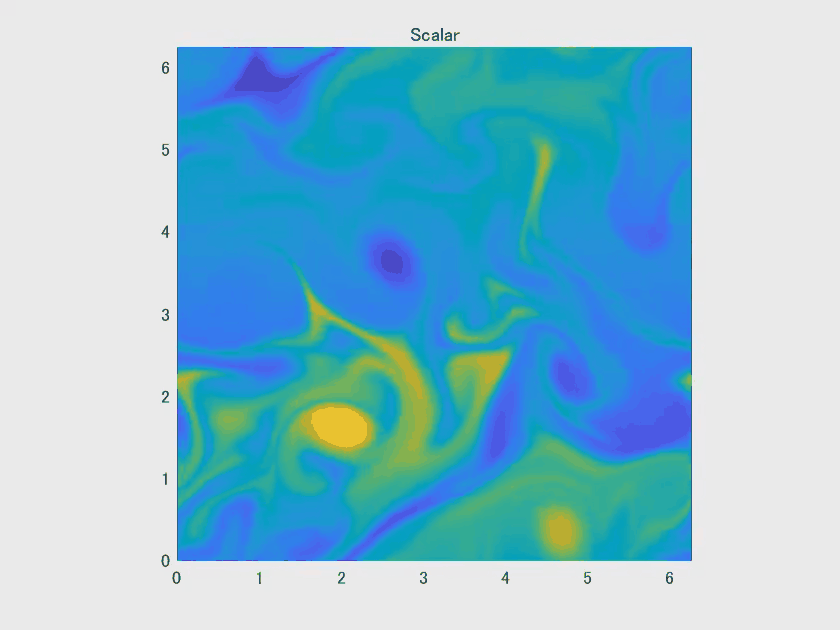
最终，在循环结束后，代码会显示标量场的变化并打印出 CFL 数等关键信息。

2. 涉及的理论

该案例涉及多个计算流体力学的理论和数值方法，包括湍流建模、伪谱法、傅里叶变换、CFL条件、三阶Runge-Kutta方法，以及拉普拉斯方程的求解。

2.1 二维湍流

二维湍流在磁流体力学和地球物理流体力学（尤其是大气动力学）方向讨论的比较多

二维湍流在许多方面与三维湍流不同，其中最显著的区别是能量级联方向的差异。

在三维湍流中，能量从大尺度传递到小尺度（称为正能量级联），最终由于粘性作用而耗散。

而在二维湍流中，能量级联有两个方向：

  • 正能量级联：从大尺度向小尺度传递，与三维湍流相似。

  • 逆能量级联：从小尺度向大尺度传递，这在三维湍流中并不存在。

由于逆能量级联的存在，二维湍流通常会形成大尺度的涡旋结构，就如同本文案例中所展现的效果。

2.2 伪谱法（Pseudo-spectral Method）

伪谱法（拟谱法 ） 是一种数值方法，用于求解偏微分方程，特别是对流和扩散问题。在伪谱法中，非线性项在物理空间中计算，然后通过傅里叶变换转换到频率空间，以便利用快速傅里叶变换（FFT）高效地计算空间导数。

伪谱法的基本步骤如下：

  1. 初始条件：定义物理空间中的场变量（如速度、标量）。

  2. 傅里叶变换：将场变量从物理空间转换到频域。

  3. 计算导数：在频域计算空间导数。

  4. 傅里叶逆变换：将结果转换回物理空间，以更新场变量。

  5. 时间推进：根据时间积分方案更新场变量。

伪谱法的优点是可以精确地计算导数（由于傅里叶变换的精度），但缺点是容易受到高频噪声的影响，因此通常需要使用滤波器来控制误差。

2.3 傅里叶变换（Fourier Transform）

傅里叶变换是一种将函数从时域或空间域转换到频域或波数域的方法。对于离散数据，使用的是离散傅里叶变换（DFT），其快速实现版本为快速傅里叶变换（FFT）。在湍流模拟中，傅里叶变换的作用包括：

  • 频率空间的导数计算：在频率空间中，空间导数可以通过乘以虚数单位1i和波数k来实现。

  • 解析偏微分方程：许多方程（如拉普拉斯方程）在频率空间中更容易解析。

在代码中，傅里叶变换用于计算速度场和涡度场的导数，以及解拉普拉斯方程来得到流函数。

2.4 CFL条件（CFL Condition）

CFL条件（Courant–Friedrichs–Lewy 条件）是数值模拟中的稳定性条件。它决定了时间步长dt必须足够小，以确保解的稳定性。

具体而言，CFL条件要求：

最大速度

代码中每20步重新计算 CFL 数，用于调整时间步长dt，以确保数值模拟的稳定性。

2.5 三阶Runge-Kutta方法

Runge-Kutta方法是一类用于求解常微分方程的数值积分方法。三阶Runge-Kutta方法是一种高级的时间积分方案，具有较高的精度和稳定性。

本文介绍的案例中使用的方案有以下三个子步骤：

  1. 计算初始梯度，并更新场变量。

  2. 基于第一次更新的结果，计算第二次更新。

  3. 使用前两次更新的结果，计算最终的场变量。

这种方法可以有效地降低数值误差，并且适用于复杂的非线性系统。

2.6 拉普拉斯方程的求解

拉普拉斯方程是流体动力学中的常见方程，用于描述势场。

对于二维涡量方程，可以通过解拉普拉斯方程得到流函数 ：

在频率空间中，拉普拉斯方程可以简化为代数方程：

其中 ：k^2 是波数（Wavenumber）的平方， 表示流函数在频域中的表示。

在代码中，通过 idel2（即 -1/k^2）计算 。

2.7 能量和耗散

湍流模拟中，能量的传递和耗散是关键要素。通过波数 k 的调整，代码中引入了强制项和大尺度耗散项，以模拟真实湍流中能量的输入和耗散：

  • 强制项：在中等尺度上，代码通过调整 kk 来引入能量（对应于物理上能量的输入）。

  • 大尺度耗散：在大尺度上，通过增加 kk 的值来增强耗散，从而防止大尺度能量的积累。

这种方法在湍流研究中非常普遍，用于保持数值稳定性并模仿实际物理现象。

关注公众号：资源充电吧

公众号回复 ：学习

一起来交流吧

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2085841.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

驱动开发系列14 - Wayland 详解

驱动开发系列14 - Wayland 详解

目录 一：概述 二：操作系统如何支持 Wayland 三：显卡驱动如何支持 Wayland 四：Wayland 协议介绍 一：概述 Wayland 是一种通信协议，规定了显示服务器与其客户端之间的通信，以及该协议的 C 语言库实现。使用 Wayland 协议的显示服务器称为 Wayland 合成器，因…
阅读更多...
SpringBoot项目中mybatis执行sql很慢的排查改造过程（Interceptor插件、fetchSize、隐式转换等）

SpringBoot项目中mybatis执行sql很慢的排查改造过程（Interceptor插件、fetchSize、隐式转换等）

刚入职公司&#xff0c;就发现公司项目跑sql特别慢&#xff0c;差不多一万条数据插入到数据库要5秒以上&#xff08;没有听错&#xff0c;就是这个速度&#xff09;&#xff0c;查询修改删除也是特别慢。直到22年年底实在是受不了了&#xff0c;我就去排查了一下。 用的是Oracl…
阅读更多...
大模型之二十八-语音识别Whisper进阶

大模型之二十八-语音识别Whisper进阶

在上一篇博客大模型之二十七-语音识别Whisper实例浅析中遗留了几个问题&#xff0c;这里来看一下前两个问题。 1.如果不是Huggingface上可以下载的数据该怎么办&#xff1f; 2.上面的代码是可以训练了&#xff0c;但是训练的时候loss真的会和我们预期一致吗&#xff1f;比如如下…
阅读更多...
【netty系列-08】深入Netty组件底层原理和基本实现

【netty系列-08】深入Netty组件底层原理和基本实现

Netty系列整体栏目 内容链接地址【一】深入理解网络通信基本原理和tcp/ip协议https://zhenghuisheng.blog.csdn.net/article/details/136359640【二】深入理解Socket本质和BIOhttps://zhenghuisheng.blog.csdn.net/article/details/136549478【三】深入理解NIO的基本原理和底层…
阅读更多...
第一个go程序

第一个go程序

package main import "fmt" func main(){fmt.Println("Hello World") }hello.go所在目录 运行go程序
阅读更多...
美团代付多模版三合一源码 附教程

美团代付多模版三合一源码 附教程

简介 美团代付多模版三合一源码 附教程 界面
阅读更多...
这一轮医疗数字化，沃可趣以医疗专业人员交流成长为中心

这一轮医疗数字化，沃可趣以医疗专业人员交流成长为中心

沃可趣看见医疗行业人员需求痛点&#xff0c;量身打造数字服务平台&#xff0c;促进知识分享&#xff0c;赋能活动组织。 从电子病历的普及到远程医疗的兴起&#xff0c;从人工智能辅助诊断到大数据在医疗管理中的应用&#xff0c;科技进步正在大力推动医疗领域的发展。然而&a…
阅读更多...
Ubuntu系统本地搭建WordPress网站并一键发布内网站点至公网实战

Ubuntu系统本地搭建WordPress网站并一键发布内网站点至公网实战

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
嵌入式技术文件、学习资料、在线工具、学习网站、技术论坛，非常全面的分享~~~

嵌入式技术文件、学习资料、在线工具、学习网站、技术论坛，非常全面的分享~~~

一、数据手册查询及下载网站 1、【ALLDATASHEET 自称是最大的在线电子元件数据的搜索引擎】ALLDATASHEETCN.COM - 电子元件和半导体及其他半导体的数据表搜索网站。电子元件和半导体, 集成电路, 二极管, 三端双向可控硅 和其他半导体的https://www.alldatasheetcn.com/ 2、【…
阅读更多...
defineProps、defineEmits、 defineExpose的TS写法

defineProps、defineEmits、 defineExpose的TS写法

小满视频 1 defineProps&#xff1a;父向子传递数据 作用&#xff1a;父组件向子组件传递数据 1.1 传递纯类型参数的方式来声明 父组件中的代码&#xff1a; 父组件App.vue <template><div><span>传递给子组件的响应式数据&#xff1a;</span>&l…
阅读更多...
【循环顺序队的实现】

【循环顺序队的实现】

1.队列的逻辑结构 与 抽象数据类型定义 先进先出的线性表 在顺序队列中&#xff0c;我们使用头指针front指向队首元素&#xff1b;用尾指针rear指向队尾元素的下一个位置&#xff08;当然这里的指针是用下标模拟出来的&#xff09; 同时顺序队列中的元素当然是用数组来存储的 …
阅读更多...
【系统架构设计】嵌入式系统设计（1）

【系统架构设计】嵌入式系统设计（1）

【系统架构设计】嵌入式系统设计&#xff08;1&#xff09; 嵌入式系统概论嵌入式系统的组成硬件嵌入式处理器总线存储器I/O 设备与接口 软件 嵌入式开发平台与调试环境交叉平台开发环境交叉编译环境调试 嵌入式网络系统嵌入式数据库管理系统实时系统与嵌入式操作系统嵌入式系统…
阅读更多...
【Qt笔记】QToolButton控件详解

【Qt笔记】QToolButton控件详解

目录 一、前言 二、QToolButton的基本特性 2.1 图标和文本 2.2 自动提升 2.3 下拉菜单 2.4 工具提示 2.5 弹出模式 三、高级功能 3.1 自定义大小与形状 3.2 检查框与单选按钮 3.3 动画效果 四、常用方法与信号槽 常用方法 信号槽 五、实际应用示例 说明 六、总…
阅读更多...
ESP32 CYD 使用 LVGL 在屏幕上显示图像 | Random Nerd Tutorials

ESP32 CYD 使用 LVGL 在屏幕上显示图像 | Random Nerd Tutorials

在本指南中&#xff0c;你将学习如何使用LVGL在ESP32 Cheap Yellow Display (CYD) 板上处理和加载图像。ESP32将使用Arduino IDE进行编程。 对ESP32 Cheap Yellow Display不熟悉&#xff1f; 从这里开始&#xff1a;开始使用ESP32 Cheap Yellow Display Board – CYD (ESP32-2…
阅读更多...
线性代数 第三讲 线性相关无关 线性表示

线性代数 第三讲 线性相关无关 线性表示

线性代数 第三讲 线性相关无关 线性表示 文章目录 线性代数 第三讲 线性相关无关 线性表示1.向量运算1.线性相关与线性无关1.1 线性相关与线性无关基本概念 2.线性表示&#xff08;线性组合&#xff09;3.线性相关无关与线性表示的定理大总结3.1 向量β可由向量组线性表出的同义…
阅读更多...
心觉：潜意识显化很简单，只是很多人想复杂了

心觉：潜意识显化很简单，只是很多人想复杂了

很多人知道潜意识的力量很大&#xff0c;是意识力量的30000倍以上 也知道该怎么显化自己的潜意识 但是就是做不到 这就像很多肥胖的人知道运动可以减肥 知道减肥之后就可以穿漂亮的衣服 知道减肥之后自己有多帅多美 但是就是迈不开腿 根本原因是你的潜意识和意识上的认知不…
阅读更多...
RenderMan v26.2更新内容！云渲染平台支持新版本

RenderMan v26.2更新内容！云渲染平台支持新版本

皮克斯的最新RenderMan v26.2版本带来了一系列激动人心的新特性和改进&#xff0c;进一步巩固了其在高端渲染领域的领导地位&#xff0c;为艺术家们提供了更丰富的创意工具和更流畅的工作流程。作为老牌的云渲染农场&#xff0c;瑞云依然支持新版本的使用。 RenderMan v26.2更新…
阅读更多...
移动端视频编辑SDK解决方案，关键帧曲线塑造生动效果

移动端视频编辑SDK解决方案，关键帧曲线塑造生动效果

美摄科技&#xff0c;作为移动视频编辑技术的领航者&#xff0c;携其革命性的移动端视频编辑SDK解决方案&#xff0c;正以前所未有的创新力&#xff0c;为视频创作者们开启了一扇通往无限创意的大门。 重塑视频编辑体验&#xff0c;让创意触手可及 美摄科技的移动端视频编辑S…
阅读更多...
公网信息泄露监测（网盘、暗网、搜索引擎、文档平台）思路分享

公网信息泄露监测（网盘、暗网、搜索引擎、文档平台）思路分享

一、背景 众测项目中白帽可能会提交一些信息泄露漏洞&#xff0c;同时甲方可会收到一些白帽提交的公网信息泄露文件漏洞&#xff0c;例如百度网盘被员工分享某些文件或者某些包含敏感信息的文件可以通过如谷歌、百度等搜索引擎通过特定语法搜索到。为了可以及时发现泄露的文件…
阅读更多...
九泰智库 | 医械周刊- Vol.54

九泰智库 | 医械周刊- Vol.54

⚖️ 法规动态 国家药监局综合司发布医疗器械管理法草案征求意见稿 国家药监局综合司发布了《中华人民共和国医疗器械管理法&#xff08;草案征求意见稿&#xff09;》&#xff0c;公开征求意见&#xff0c;以加强医疗器械的管理并推动产业高质量发展。该草案共十一章190条&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023