【MATLAB学习笔记】绘图——自定义标记(Marker)形状，实现与MATLAB自带标记基本一致的功能(自适应缩放、自适应裁剪)

news2024/9/19 19:47:26

目录

  • 前言
  • 自定义标记函数
  • 自定义标记函数的说明
    • 纵横比调整
    • 将图形大小按磅数设置
    • 平移标记点
    • 绘制标记点
    • 边界标记点不裁剪
  • 拓展功能——标记点自适应绘图区的缩放
    • 绘图区缩放回调函数
    • 标记点大小自适应
    • 标记点裁剪自适应
  • 示例
    • 基本绘图
    • 自定义标记函数的使用
  • 总代码
    • 主函数
    • 自定义标记函数
    • 回调函数
    • 其他函数
  • 总结

前言

  在MATLAB中，使用plot、scatter和patch等函数进行绘图时，很多时候都需要使用标记(Marker)对数据点进行标记，以便更清晰地展示数据。在MATLAB只能使用默认的标记形状(如下图)，但有时觉得MATLAB自带的标记不好看或者不够用时就需要自定义标记形状，而MATLAB中并没有提供自定义标记这样一个功能或者函数。
在这里插入图片描述

  本文章提供了一个可以自定义标记形状的函数，只需要输入标记形状的点坐标和连接方式即可绘制出与MATLAB自带标记基本一致的自定义标记，包括随着绘图区的缩放，标记在屏幕上的大小不会改变，以及绘图区边缘的标记可以超出绘图区等功能，同时可以设置该标记的颜色、磅数、线宽等基本属性。

自定义标记函数

  自定义标记的主函数如下，该函数目前只能绘制没有交叉线的图形。前5个参数为必须输入，包括ax绘图区对象，曲线的x和y坐标，标记形状的点坐标GPoints(第一列为x坐标，第二列为y坐标)，形状点的连接顺序(不需要首尾相连)GSeq。
  其他可设置参数为填充的面颜色faceColor，填充的线颜色edgeColor，形状的大小pounds，形状的线宽度lineWidth，形状的数量NMarker(近似数量, 采用等间距, 如不能整除则四舍五入，输入0则表示绘制所有点的标记)。同时，若不需要则以空数组[ ]代替, 如不需要形状磅数pounds, 则pounds = [ ]。

function setMarker(ax, x, y, GPoints, GSeq, faceColor, edgeColor, pounds, lineWidth, NMarker)
% 自定义设置标记形状(目前只能绘制没有交叉线的图形), 前5个参数为必须输入, 其他参数为可选参数
% 若不需要则以空数组[]代替, 如不需要形状磅数pounds, 则pounds = []
%
% ax        绘图区
% x,y       绘图的数据点
% GPoints   形状的点坐标
% GSeq      形状点的连接顺序(不需要首尾相连)
% faceColor 填充的面颜色  默认:none
% edgeColor 填充的线颜色  默认:k
% pounds    形状的大小(磅数)  默认:6
% lineWidth 形状的线宽度  % 默认:0.5
% NMarker   形状的数量(近似数量, 采用等间距, 如不能整除则四舍五入)  
%           默认:0, 0则代表全部点都绘制

if nargin < 6, faceColor = 'none'; end
if nargin < 7, edgeColor = 'k'; end
if nargin < 8, pounds = 6; end
if nargin < 9, lineWidth = 0.5; end
if nargin < 10, NMarker = 0; end

if isempty(faceColor), faceColor = 'none'; end
if isempty(edgeColor), edgeColor = 'k'; end
if isempty(pounds), pounds = 6; end
if isempty(lineWidth), lineWidth = 0.5; end
if isempty(NMarker), NMarker = 0; end

if NMarker == 0, NMarker = length(x); end

hold(ax,"on") 

NG = length(GSeq);  % 点数量

% 将图形的比例拉正
xl = xlim;
yl = ylim;
lenx = xl(2)-xl(1); % x轴的长度
leny = yl(2)-yl(1); % y轴的长度
yRatio = leny/lenx; % 纵横比比例
GPoints(:,2) = GPoints(:,2)*yRatio; % 修正坐标 

% 获取绘图区的每单位在屏幕上的长度(磅)
unitLength = getUnitLength();

% 计算水平距离矩阵
W = zeros(NG);
for i = 1:NG
    for j = 1:NG
        if i ~= j
            W(i,j) = sqrt((GPoints(i,1)-GPoints(j,1))^2);
        end
    end
end

% 缩放比例
scale = 2*pounds/(max(max(W))*unitLength);
% 缩放
GPoints = GPoints*scale;

PM = 1:round(length(x)/NMarker):length(x);   % 需要绘制的点位置
NMarker = length(PM);                        % 绘制标记的真实数量

% 重心坐标
[Cx, Cy] = polygon_centroid(GPoints);

% 初始化所有标记的坐标和连接顺序
GPointsAll = zeros(NMarker*NG,2);
GSeqAll = zeros(NMarker,NG);
% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标和连接顺序
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;
    GSeqAll(k,:) =  GSeq + NG*(k-1);

    %%% 判断当前标记点是否处于边界 %%%
    xkk = GPointsNew(:, 1);  % 当前标记点的x坐标
    ykk = GPointsNew(:, 2);  % 当前标记点的y坐标
    
    % 标记形状坐标判断
    BLeft = xkk - xl(1);    % 左边界
    BRight = xkk - xl(2);   % 右边界
    BDown = ykk - yl(1);    % 下边界
    BUp = ykk - yl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - xl(1);    % 左边界
    BRight2 = xl(2)-xk;     % 右边界
    BDown2 = yk - yl(1);    % 下边界
    BUp2 = yl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>=0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end
    
end
% 绘制标记点
pa = patch('Faces', GSeqAll, 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'lineWidth',lineWidth);

% 设置绘图区边缘图形不裁剪
pa2 = patch('Faces', GSeqAll(BJudge,:), 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth, 'Clip', 'off');

%%%% 控制图形放大缩小 %%%%
zm = zoom(ax);
zm.Enable = 'on'; % 启用缩放

% 初始化xy轴范围
xl = xlim;
yl = ylim;
setappdata(ax,'lxl',xl) 
setappdata(ax,'lyl',yl) 

% 绘图区缩放回调函数
set(zm, 'ActionPostCallback', @(src, event) updateZoomInfo(ax,x,y,PM,NG,NMarker,pa,pa2)); 

end

自定义标记函数的说明

纵横比调整

  在自定义形状时，如果x轴和y轴的刻度一致，则绘制出来的图形与实际一致。大多数情况下，MATLAB绘制图形时一般x轴和y轴的刻度并不一致，比如x轴一格长度为2，y轴一格长度为500，这时绘制出来的图形看起来会呈现上下被压扁的性质。比如，原本需要绘制的形状是下图这个四边形，但是因为x轴和y轴的刻度不一致，会出现绘制出来的形状只呈现出一条线(下面第二张图)。
在这里插入图片描述
在这里插入图片描述
  为了避免这种情况，首先就要对图形比例进行修正，即获取x轴和y轴刻度之间的比例，对标记图形的x或者y坐标进行拉伸或者收缩。

% 将图形的比例拉正
xl = xlim;
yl = ylim;
lenx = xl(2)-xl(1); % x轴的长度
leny = yl(2)-yl(1); % y轴的长度
yRatio = leny/lenx; % 纵横比比例
GPoints(:,2) = GPoints(:,2)*yRatio; % 修正坐标

下面是调整后的效果图。
在这里插入图片描述

将图形大小按磅数设置

  放缩了x轴或者y轴的比例后，会出现标记图形过大或者过小的情况，这时就需要对标记的坐标进行放缩。在MATLAB中，标记的大小(MarkerSize)通常以磅数为单位，默认大小为6磅。同样参考MATLAB的方式，我们绘制图形也可以用磅数设置图形大小，但并不知道绘图区单位长度对应的磅数大小是多少。因此，首先要计算绘图区中的单位磅数。
  下面的函数中，Position(3)对应的就是x轴的总磅数，除x轴的总长度即可得到绘图区中的单位磅数。在上图中，绘图区中的单位磅数为50.9091磅。

function unitLength = getUnitLength()
% 获取绘图区的每单位在屏幕上的长度(磅)
   
% 获取图形窗口的大小和位置  
Po = get(gcf, 'Position'); % 返回的单位是点 (points)，每个点约为 1/72 英寸  
figWidth = Po(3); % 图形的宽度 

% X轴范围  
xl = xlim;
rangeX = xl(2) - xl(1); 

% 绘图区的每单位在屏幕上的长度(磅)
unitLength = figWidth/rangeX;

end

  得到了绘图区中的单位磅数后就可以以某一个标准(比如图形的水平长度、竖直长度和最长边的长度等)对图形的坐标进行放缩。本文采用图形的水平长度L为标准，将长度L乘单位长度unitLength可以得到图形当前的磅数，由于MATLAB中图形的大小是以半径为参考的，故需要在前面乘2。

% 获取绘图区的每单位在屏幕上的长度(磅)
unitLength = getUnitLength();

% 水平长度矩阵
L = max(GPoints(:,1)) - min(GPoints(:,1));

% 缩放比例
scale = 2*pounds/(L*unitLength);

% 缩放
GPoints = GPoints*scale;

  设置磅数pounds = 6，可以得到下面的效果图(红色为自定义标记，黑色为MATLAB自带的三角形标记)，可以看到，自定义标记与MATLAB自带标记的大小一致。
在这里插入图片描述

平移标记点

  已知标记点初始的点坐标和连接顺序后，还需要将标记点平移到相应的位置。
  NMarker为需要绘制的标记点数量，为得到标记点的位置，需要将整个数据区间均分成NMarker份。但是，输入的NMarker并不一定能均分，因此文章采用一种四舍五入的方法，即下面的round(length(x)/NMarker)，以及更新NMarker的数量。

% 计算绘制的点位置
PM = 1:round(length(x)/NMarker):length(x);   % 需要绘制的点位置
NMarker = length(PM);                        % 绘制标记的真实数量

  得到了绘制标记点的位置后，需要将标记平移到该位置。本文以标记图形的重心作为参考，计算重心到该位置的位移，再到坐标进行更新。
  计算多边形的重心方法如下：

  1. 计算面积 A A A
      假设一个多边形的顶点坐标为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) (x1​,y1​),(x2​,y2​),…,(xn​,yn​)，连接顺序为 1 − n − 1 1-n-1 1−n−1，则该多边形的面积 A A A为
    A = 1 2 ∣ ∑ i = 1 n ( x i y i + 1 − x i + 1 y i ) ∣ A = \frac{1}{2} \left| \sum_{i=1}^{n} (x_i y_{i+1} - x_{i+1} y_i) \right| A=21​ ​i=1∑n​(xi​yi+1​−xi+1​yi​) ​其中 ( x n + 1 , y n + 1 ) (x_{n+1}, y_{n+1}) (xn+1​,yn+1​)被定义为 ( x 1 , y 1 ) (x_1, y_1) (x1​,y1​)。
  2. 计算重心的坐标 ( C x , C y ) (C_x, C_y) (Cx​,Cy​)
      重心 C C C的坐标 ( C x , C y ) (C_x, C_y) (Cx​,Cy​)可通过以下公式计算：
    C x = 1 6 A ∑ i = 1 n ( x i + x i + 1 ) ( x i y i + 1 − x i + 1 y i ) C y = 1 6 A ∑ i = 1 n ( y i + y i + 1 ) ( x i y i + 1 − x i + 1 y i ) C_x = \frac{1}{6A} \sum_{i=1}^{n} (x_i + x_{i+1})(x_i y_{i+1} - x_{i+1} y_i) \\ C_y = \frac{1}{6A} \sum_{i=1}^{n} (y_i + y_{i+1})(x_i y_{i+1} - x_{i+1} y_i) Cx​=6A1​i=1∑n​(xi​+xi+1​)(xi​yi+1​−xi+1​yi​)Cy​=6A1​i=1∑n​(yi​+yi+1​)(xi​yi+1​−xi+1​yi​)根据上面的计算过程，计算重心的函数polygonCentroid如下：
function [Cx, Cy] = polygonCentroid(points)  
% 计算形状的重心坐标
% points 一个n x 2 的矩阵, 表示n个点的坐标, 第一列为x值, 第二列为y值  

% 点的数量  
n = size(points, 1);  

% 闭合多边形  
points = [points; points(1, :)];  

% 初始化面积和重心坐标  
A = 0;  
Cx = 0;  
Cy = 0;  

% 计算面积和重心坐标  
for i = 1:n  
    xi = points(i, 1);  
    yi = points(i, 2);  
    xi1 = points(i+1, 1);  
    yi1 = points(i+1, 2);  
    
    % 计算有向面积  
    A_temp = xi * yi1 - xi1 * yi;  
    A = A + A_temp;  

    % 计算重心坐标  
    Cx = Cx + (xi + xi1) * A_temp;  
    Cy = Cy + (yi + yi1) * A_temp;  
end  

A = A / 2; % 最终面积取绝对值  
Cx = Cx / (6 * A);  
Cy = Cy / (6 * A);  
  
end

  得到了重心坐标后，接着进行平移。GPointsAll和GSeqAll用于存储所有标记点的坐标和连接方式，方便一次性绘图，在循环中绘图会影响绘图速度。

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标和连接顺序
GPointsAll = zeros(NMarker*NG,2);
GSeqAll = zeros(NMarker,NG);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标和连接顺序
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;
    GSeqAll(k,:) =  GSeq + NG*(k-1);
 
end

绘制标记点

  绘制标记点采用patch函数，patch函数其中一个用法如下：

  • patch(‘Faces’,F,‘Vertices’,V) 创建一个或多个多边形，其中 V 指定顶点的值，F 定义要连接的顶点。

  FaceColor、EdgeColor和LineWidth分别表示面的颜色、线的颜色和线的宽度。此外，patch是MATLAB中绘制多边形非常强大的函数，其他用途可以参考下面这几篇文章。
【MATLAB学习笔记】绘图——errorbar误差图+patch误差填充图
【有限元学习笔记】二维四边形单元位移云图可视化(有限元后处理)——MATLAB程序
【有限元学习笔记】二维四边形单元应力动画云图可视化(高斯点应力外推、应力绕节点平均)——MATLAB程序

% 绘制标记点
pa = patch('Faces', GSeqAll, 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth);

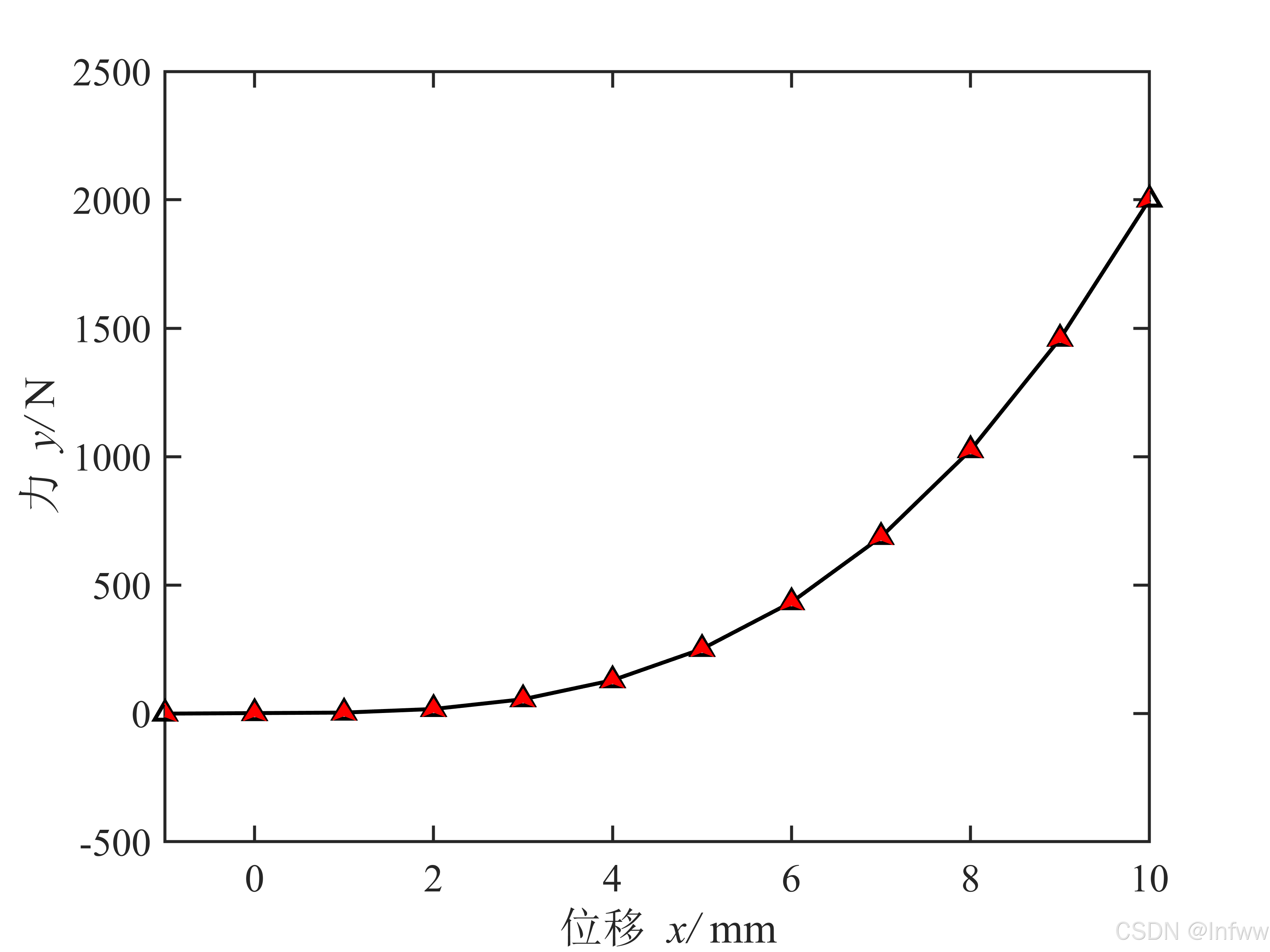
在这里插入图片描述

边界标记点不裁剪

  此外，注意到处于边界处的标记点(红色)被边界裁剪了，而MATLAB自带的标记点(黑色)并没有被裁剪。
在这里插入图片描述
  要想实现这个效果只需要将patch中的Clipping属性设置为 “off” 即可。

% 绘制标记点
pa = patch('Faces', GSeqAll, 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth, 'Clipping', 'off');

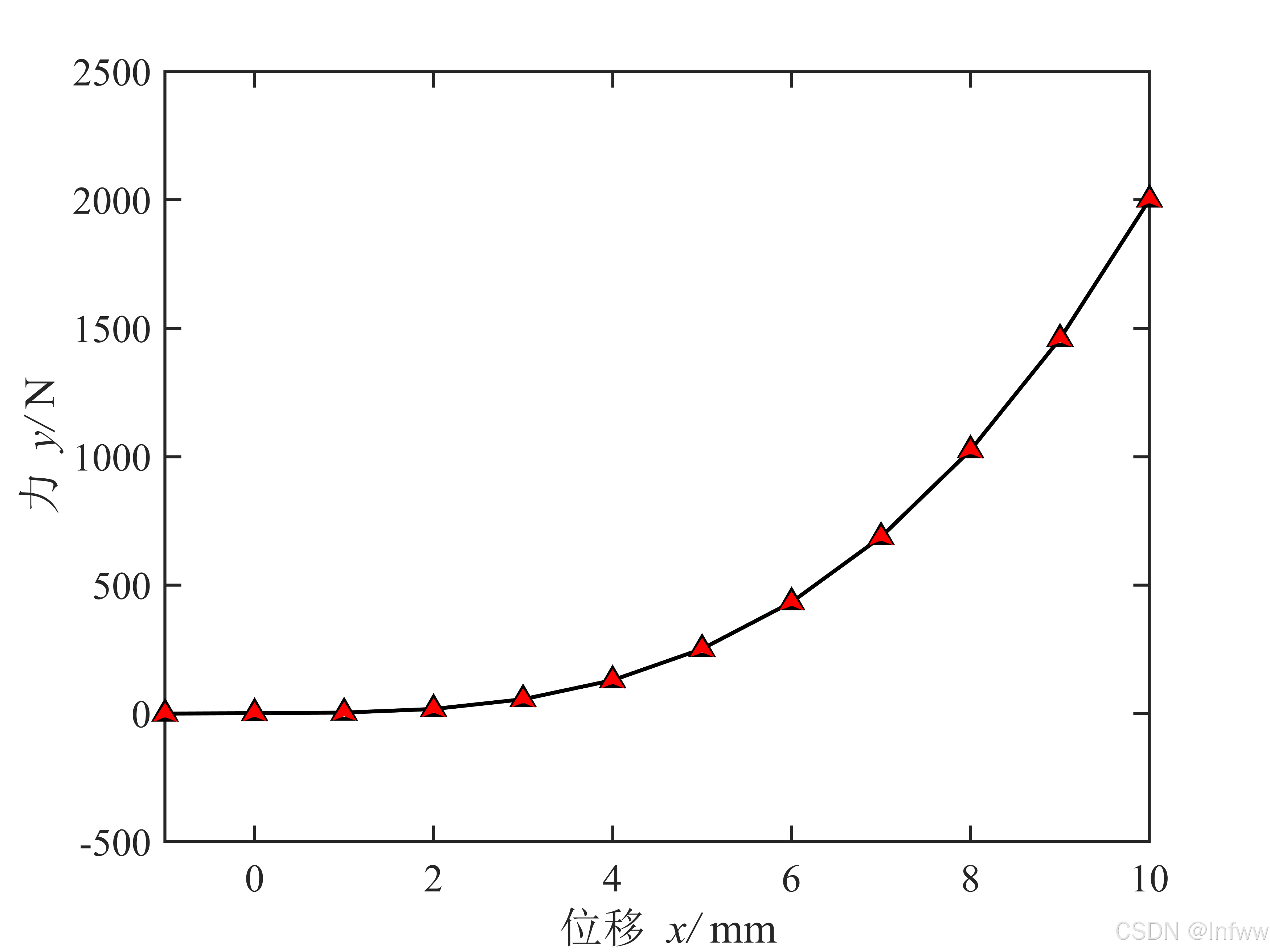
在这里插入图片描述

拓展功能——标记点自适应绘图区的缩放

绘图区缩放回调函数

  要想标记点自适应绘图区的缩放而变化，就需要采用回调函数对一些参数进行更改。简单来说，回调函数就是用户在执行某一项操作时自动执行的函数。
  下面利用回调函数监控了绘图区的缩放，当绘图区进行缩放时就会自动执行updateZoomInfo这个函数。setappdata函数可以将变量数据动态保存，方便在updateZoomInfo函数中使用这个数据，下面代码中保存了x轴范围xl和y轴范围yl。

%%%% 控制图形放大缩小 %%%%
zm = zoom(ax);
zm.Enable = 'on'; % 启用缩放

% 初始化xy轴范围
xl = xlim;
yl = ylim;
setappdata(ax,'lxl',xl) 
setappdata(ax,'lyl',yl) 

% 绘图区缩放回调函数
set(zm, 'ActionPostCallback', @(src, event) updateZoomInfo(ax,x,y,PM,NG,NMarker,pa,pa2));

回调函数updateZoomInfo的代码如下：

function updateZoomInfo(ax,x,y,PM,NG,NMarker,pa,pa2)  
% 监控绘图区缩放并自动更新标记图形的回调函数
%
% ax        绘图区
% x,y       绘图的数据点
% PM        需要绘制的点位置
% NG        % 点数量
% NMarker   形状的数量
% pa        patch对象
% pa2       边缘点的patch对象

% 当前xy轴范围   
cxl = xlim(ax); 
cyl = ylim(ax);

% 获取上一次缩放的xy轴范围
lxl = getappdata(ax,'lxl');
lyl = getappdata(ax,'lyl');
% 保存当前的xy轴范围
setappdata(ax,'lxl',cxl)
setappdata(ax,'lyl',cyl)

% 计算xy轴放大因子
xScaleFactor = (lxl(2) - lxl(1))/(cxl(2) - cxl(1));  
yScaleFactor = (lyl(2) - lyl(1))/(cyl(2) - cyl(1));

% 获取当前的节点坐标和连接顺序
GPoints = pa.Vertices;
GSeq = pa.Faces;
GPoints = GPoints(1:NG,:);

% 缩放坐标
GPoints(:,1) = GPoints(:,1)/xScaleFactor;
GPoints(:,2) = GPoints(:,2)/yScaleFactor;

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标
GPointsAll = zeros(NMarker*NG,2);
% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;

    %%% 判断当前标记点是否处于边界 %%%
    % 标记形状坐标判断
    BLeft = GPointsNew(:, 1) - cxl(1);    % 左边界
    BRight = GPointsNew(:, 1) - cxl(2);   % 右边界
    BDown = GPointsNew(:, 2) - cyl(1);    % 下边界
    BUp = GPointsNew(:, 2) - cyl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - cxl(1);    % 左边界
    BRight2 = cxl(2)-xk;     % 右边界
    BDown2 = yk - cyl(1);    % 下边界
    BUp2 = cyl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end
    
end

% 更新坐标
pa.Vertices = GPointsAll;

% 设置绘图区边缘图形不裁剪
pa2.Vertices = GPointsAll;
pa2.Faces = GSeq(BJudge,:);

end

标记点大小自适应

  在缩放绘图区时，自定义标记的大小并不会自己改变，而MATLAB自带的标记大小会自动更新，如下图。
在这里插入图片描述
  要想实现这种效果就需要在回调函数中计算当前x轴和y轴的放大比例，在对标记点的坐标进行缩放。其中getappdata表示获取上一次缩放的x轴和y轴范围，setappdata保存当前的x轴和y轴范围。计算得到了放大因子后，对标记图形的x坐标和y坐标分别缩放即可。

% 当前xy轴范围   
cxl = xlim(ax); 
cyl = ylim(ax);

% 获取上一次缩放的xy轴范围
lxl = getappdata(ax,'lxl');
lyl = getappdata(ax,'lyl');
% 保存当前的xy轴范围
setappdata(ax,'lxl',cxl)
setappdata(ax,'lyl',cyl)

% 计算xy轴放大因子
xScaleFactor = (lxl(2) - lxl(1))/(cxl(2) - cxl(1));  
yScaleFactor = (lyl(2) - lyl(1))/(cyl(2) - cyl(1));

% 获取当前的节点坐标和连接顺序
GPoints = pa.Vertices;
GSeq = pa.Faces;
GPoints = GPoints(1:NG,:);

% 缩放坐标
GPoints(:,1) = GPoints(:,1)/xScaleFactor;
GPoints(:,2) = GPoints(:,2)/yScaleFactor;

  得到了缩放后的坐标后，需要重新计算新的平移位置。其中%%% 判断当前标记点是否处于边界 %%%部分见下一小节。

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标
GPointsAll = zeros(NMarker*NG,2);
% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;

    %%% 判断当前标记点是否处于边界 %%%
    % 标记形状坐标判断
    BLeft = GPointsNew(:, 1) - cxl(1);    % 左边界
    BRight = GPointsNew(:, 1) - cxl(2);   % 右边界
    BDown = GPointsNew(:, 2) - cyl(1);    % 下边界
    BUp = GPointsNew(:, 2) - cyl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - cxl(1);    % 左边界
    BRight2 = cxl(2)-xk;     % 右边界
    BDown2 = yk - cyl(1);    % 下边界
    BUp2 = cyl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end
    
end

  最后，更新一下patch中的点数据。

% 更新坐标
pa.Vertices = GPointsAll;

  放大后的效果图如下。可见，随着绘图区的缩放，自定义标记在屏幕上的大小并不会发生改变，与MATLAB自带的标记一致。
在这里插入图片描述

标记点裁剪自适应

  将原本patch中的Clipping属性设置为 “off”，虽然在初始图形中显示为不裁剪，但是在图形放大时会出现标记点偏离绘图区很多的情况，如下图。
应
  因此，不能直接将原来的patch函数中的Clipping属性设置为 “off” ，而是需要创建一个新的patch函数，只针对边界处的标记点设置成不裁剪模式。首先，需要判断标记点是否处于边界处，判断准则有两个：

  1. 重心点位于绘图区内；
  2. 标记图形的任意点超出绘图区。

  基于此准则，将平移标记点部分的最后一个代码块修改如下(回调函数部分的也是如此，只不过该部分在上一小节中已经提前改好了)。其中BJudge用于判断该标记点是否处于边界处，若处于边界处则为true，反之则为false。

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标和连接顺序
GPointsAll = zeros(NMarker*NG,2);
GSeqAll = zeros(NMarker,NG);

% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标和连接顺序
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;
    GSeqAll(k,:) =  GSeq + NG*(k-1);

    %%% 判断当前标记点是否处于边界 %%%   
    % 标记形状坐标判断
    BLeft = GPointsNew(:, 1) - xl(1);    % 左边界
    BRight = GPointsNew(:, 1) - xl(2);   % 右边界
    BDown = GPointsNew(:, 2) - yl(1);    % 下边界
    BUp = GPointsNew(:, 2) - yl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - xl(1);    % 左边界
    BRight2 = xl(2)-xk;     % 右边界
    BDown2 = yk - yl(1);    % 下边界
    BUp2 = yl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>=0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end 
    
end

  上面代码中的judgeSign为判断数组中的元素是否为同号的函数，如果是则返回ture，反之则返回false。

function flag = judgeSign(arr) 
% 判断数组中所有元素是否同号(包含0也算同号)

    % 计算数组每个元素的符号  
    signs = sign(arr(arr~=0));  
    
    % 获取唯一符号  
    uniqueSigns = unique(signs);  
    
    % 判断是否只有一个唯一符号，并且该符号不为零  
    if length(uniqueSigns) == 1 && uniqueSigns ~= 0  
        flag = true; % 同号  
    else  
        flag = false; % 不同号或包含零  
    end  
end

  得到BJudge数组后，将边界处的标记点的’Clipping’设置为’off’。

% 设置绘图区边缘图形不裁剪
pa2 = patch('Faces', GSeqAll(BJudge,:), 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth, 'Clipping', 'off');

  最后，在回调函数中更新点数据和连接顺序。

% 设置绘图区边缘图形不裁剪
pa2.Vertices = GPointsAll;
pa2.Faces = GSeq(BJudge,:);

效果图如下，可见图形放大时不会导致出现标记点偏离绘图区很多的情况了。
在这里插入图片描述

示例

基本绘图

  下面这是基本的绘图代码，具体细节可以参考前面的文章(点击转跳)。

clc;clear;close all
set(0,'defaultfigurecolor','w');

 %% 数据
x = -1:1:10;   % 产生0到1, 步长为0.01的序列
y = 2*x.^3 + 1;    % y为x一次函数

%% 绘图
f = figure(1);
ax = gca;   % 将当前坐标区实例化
plot(x,y,'-k','LineWidth',1.3)
xlim([-1,10])

set(gca,'FontName','Times New Roman','FontSize',13)
xlabel('\fontname{宋体} 位移\fontname{Times New Roman} \it x/\rm mm')
ylabel('\fontname{宋体} 力\fontname{Times New Roman} \it y/\rm N') 

% 去除上边框、右边框刻度线
box off     % 取消边框
ax1 = axes('Position',get(ax,'Position'),'XAxisLocation','top',...
    'YAxisLocation','right','Color','none','XColor','k','YColor','k');  % 设置坐标区
set(ax1,'XTick', [],'YTick', []);   % 去掉xy轴刻度
hold off

% 保存图片
print(f,'-dpng','FigName','-r600')%保存图像

运行代码后得到下面的结果图。
在这里插入图片描述

自定义标记函数的使用

  自定义标记函数的使用非常简单，一共有两个步骤。

  1. 定义点和连接顺序
      首先，创建自定义标记的点坐标和连接顺序(不需要首尾相连)，下面提供了上文中自定义多边形标记的数据。
GPoints = [-1,-1;
           0, 1;
           1,-1;
           0,-0.5];
GSeq = 1:4;

在这里插入图片描述
2. 定义标记属性
  接着定义该形状的一些属性，不需要定义的属性则以[ ]代替。

faceColor = 'r';
edgeColor = 'r';
pounds = 6;
lineWidth = [];
NMarker = [];
setMarker(ax, x, y, GPoints, GSeq, faceColor, edgeColor, pounds, lineWidth, NMarker)

  效果图如下，最右侧的标记被右框线覆盖了一部分，解决办法可以查看下面这篇文章。
【MATLAB学习笔记】绘图——去除上、右边框刻度后图被框线覆盖解决方案
在这里插入图片描述

  • 更换形状
      形状可以自己定义，下面是一个不同于前面的形状，同样也可以绘制成功。
GPoints = [-1,-1;
           1, -0.3;
           0, 0;
           1,0.7;
           -1,1];
GSeq = 1:5;

在这里插入图片描述
在这里插入图片描述

总代码

  总代码如下，后续还会继续更新一些MATLAB绘图的技巧和细节，制作不易，别忘了关注和点赞喔。

主函数

clc;clear;close all
set(0,'defaultfigurecolor','w');

 %% 数据
x = -1:1:10;   % 产生0到1, 步长为0.01的序列
y = 2*x.^3 + 1;    % y为x一次函数

%%% 形状1
GPoints = [-1,-1;
           0, 1;
           1,-1;
           0,-0.5];
GSeq = 1:4;

% %%% 形状2
% GPoints = [-1,-1;
%            1, -0.3;
%            0, 0;
%            1,0.7;
%            -1,1];
% GSeq = 1:5;

%% 绘图
f = figure(1);
ax = gca;   % 将当前坐标区实例化
plot(x,y,'-k','LineWidth',1.3)
xlim([-1,10])

faceColor = 'r';
edgeColor = 'r';
pounds = 6;
lineWidth = [];
NMarker = [];
setMarker(ax, x, y, GPoints, GSeq, faceColor, edgeColor, pounds, lineWidth, NMarker)

set(gca,'FontName','Times New Roman','FontSize',13)
xlabel('\fontname{宋体} 位移\fontname{Times New Roman} \it x/\rm mm')
ylabel('\fontname{宋体} 力\fontname{Times New Roman} \it y/\rm N') 

% 去除上边框、右边框刻度线
box off     % 取消边框
ax1 = axes('Position',get(ax,'Position'),'XAxisLocation','top',...
    'YAxisLocation','right','Color','none','XColor','k','YColor','k');  % 设置坐标区
set(ax1,'XTick', [],'YTick', []);   % 去掉xy轴刻度
hold off

% 保存图片
print(f,'-dpng','图14','-r600')%保存图像

自定义标记函数

function setMarker(ax, x, y, GPoints, GSeq, faceColor, edgeColor, pounds, lineWidth, NMarker)
% 自定义设置标记形状(目前只能绘制没有交叉线的图形), 前5个参数为必须输入, 其他参数为可选参数
% 若不需要则以空数组[]代替, 如不需要形状磅数pounds, 则pounds = []
%
% ax        绘图区
% x,y       绘图的数据点
% GPoints   形状的点坐标
% GSeq      形状点的连接顺序(不需要首尾相连)
% faceColor 填充的面颜色  默认:none
% edgeColor 填充的线颜色  默认:k
% pounds    形状的大小(磅数)  默认:6
% lineWidth 形状的线宽度  % 默认:0.5
% NMarker   形状的数量(近似数量, 采用等间距, 如不能整除则四舍五入)  
%           默认:0, 0则代表全部点都绘制

if nargin < 6, faceColor = 'none'; end
if nargin < 7, edgeColor = 'k'; end
if nargin < 8, pounds = 6; end
if nargin < 9, lineWidth = 0.5; end
if nargin < 10, NMarker = 0; end

if isempty(faceColor), faceColor = 'none'; end
if isempty(edgeColor), edgeColor = 'k'; end
if isempty(pounds), pounds = 6; end
if isempty(lineWidth), lineWidth = 0.5; end
if isempty(NMarker), NMarker = 0; end

if NMarker == 0, NMarker = length(x); end

hold(ax,"on") 

NG = length(GSeq);  % 点数量

% 将图形的比例拉正
xl = xlim;
yl = ylim;
lenx = xl(2)-xl(1); % x轴的长度
leny = yl(2)-yl(1); % y轴的长度
yRatio = leny/lenx; % 纵横比比例
GPoints(:,2) = GPoints(:,2)*yRatio; % 修正坐标 

% 获取绘图区的每单位在屏幕上的长度(磅)
unitLength = getUnitLength();

% 水平长度矩阵
L = max(GPoints(:,1)) - min(GPoints(:,1));

% 缩放比例
scale = 2*pounds/(L*unitLength);

% 缩放
GPoints = GPoints*scale;

% 计算绘制的点位置
PM = 1:round(length(x)/NMarker):length(x);   % 需要绘制的点位置
NMarker = length(PM);                        % 绘制标记的真实数量

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标和连接顺序
GPointsAll = zeros(NMarker*NG,2);
GSeqAll = zeros(NMarker,NG);

% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标和连接顺序
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;
    GSeqAll(k,:) =  GSeq + NG*(k-1);

    %%% 判断当前标记点是否处于边界 %%%   
    % 标记形状坐标判断
    BLeft = GPointsNew(:, 1) - xl(1);    % 左边界
    BRight = GPointsNew(:, 1) - xl(2);   % 右边界
    BDown = GPointsNew(:, 2) - yl(1);    % 下边界
    BUp = GPointsNew(:, 2) - yl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - xl(1);    % 左边界
    BRight2 = xl(2)-xk;     % 右边界
    BDown2 = yk - yl(1);    % 下边界
    BUp2 = yl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>=0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end 

end
% 绘制标记点
pa = patch('Faces', GSeqAll, 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth);

% 设置绘图区边缘图形不裁剪
pa2 = patch('Faces', GSeqAll(BJudge,:), 'Vertices', GPointsAll, 'FaceColor', faceColor,...
    'EdgeColor', edgeColor,'LineWidth',lineWidth, 'Clipping', 'off');

%%%% 控制图形放大缩小 %%%%
zm = zoom(ax);
zm.Enable = 'on'; % 启用缩放

% 初始化xy轴范围
xl = xlim;
yl = ylim;
setappdata(ax,'lxl',xl) 
setappdata(ax,'lyl',yl) 

% 绘图区缩放回调函数
set(zm, 'ActionPostCallback', @(src, event) updateZoomInfo(ax,x,y,PM,NG,NMarker,pa,pa2)); 

end

回调函数

function updateZoomInfo(ax,x,y,PM,NG,NMarker,pa,pa2)  
% 监控绘图区缩放并自动更新标记图形的回调函数
%
% ax        绘图区
% x,y       绘图的数据点
% PM        需要绘制的点位置
% NG        % 点数量
% NMarker   形状的数量
% pa        patch对象
% pa2       边缘点的patch对象

% 当前xy轴范围   
cxl = xlim(ax); 
cyl = ylim(ax);

% 获取上一次缩放的xy轴范围
lxl = getappdata(ax,'lxl');
lyl = getappdata(ax,'lyl');
% 保存当前的xy轴范围
setappdata(ax,'lxl',cxl)
setappdata(ax,'lyl',cyl)

% 计算xy轴放大因子
xScaleFactor = (lxl(2) - lxl(1))/(cxl(2) - cxl(1));  
yScaleFactor = (lyl(2) - lyl(1))/(cyl(2) - cyl(1));

% 获取当前的节点坐标和连接顺序
GPoints = pa.Vertices;
GSeq = pa.Faces;
GPoints = GPoints(1:NG,:);

% 缩放坐标
GPoints(:,1) = GPoints(:,1)/xScaleFactor;
GPoints(:,2) = GPoints(:,2)/yScaleFactor;

% 重心坐标
[Cx, Cy] = polygonCentroid(GPoints);

% 初始化所有标记的坐标
GPointsAll = zeros(NMarker*NG,2);
% 边界点判断初始化
BJudge = false(NMarker,1);
for k = 1:NMarker
    % 取出当前点坐标
    xk = x(PM(k));
    yk = y(PM(k));

    % 平移
    displacement = [xk-Cx,yk-Cy];

    % 更新坐标
    GPointsNew = GPoints;
    GPointsNew = GPointsNew + repmat(displacement,size(GPoints,1),1);

    % 保存所有标记点的坐标
    GPointsAll(NG*(k-1)+1:NG*k,:) = GPointsNew;

    %%% 判断当前标记点是否处于边界 %%%
    % 标记形状坐标判断
    BLeft = GPointsNew(:, 1) - cxl(1);    % 左边界
    BRight = GPointsNew(:, 1) - cxl(2);   % 右边界
    BDown = GPointsNew(:, 2) - cyl(1);    % 下边界
    BUp = GPointsNew(:, 2) - cyl(2);      % 上边界

    % 标记中心坐标判断
    BLeft2 = xk - cxl(1);    % 左边界
    BRight2 = cxl(2)-xk;     % 右边界
    BDown2 = yk - cyl(1);    % 下边界
    BUp2 = cyl(2) - yk;      % 上边界

    % 判断形状坐标是否同号以及中心点是否在绘图区
    if (~judgeSign(BLeft) || ~judgeSign(BRight) || ~judgeSign(BDown) || ~judgeSign(BUp)) && ...
            all([BLeft2,BRight2,BDown2,BUp2]>0)
        BJudge(k) = true;  % 记录处于边界的标记点
    end
    
end

% 更新坐标
pa.Vertices = GPointsAll;

% 设置绘图区边缘图形不裁剪
pa2.Vertices = GPointsAll;
pa2.Faces = GSeq(BJudge,:);

end

其他函数

  • 计算标记图形重心函数
function [Cx, Cy] = polygonCentroid(points)  
% 计算形状的重心坐标
% points 一个n x 2 的矩阵, 表示n个点的坐标, 第一列为x值, 第二列为y值  

% 点的数量  
n = size(points, 1);  

% 闭合多边形  
points = [points; points(1, :)];  

% 初始化面积和重心坐标  
A = 0;  
Cx = 0;  
Cy = 0;  

% 计算面积和重心坐标  
for i = 1:n  
    xi = points(i, 1);  
    yi = points(i, 2);  
    xi1 = points(i+1, 1);  
    yi1 = points(i+1, 2);  
    
    % 计算有向面积  
    A_temp = xi * yi1 - xi1 * yi;  
    A = A + A_temp;  

    % 计算重心坐标  
    Cx = Cx + (xi + xi1) * A_temp;  
    Cy = Cy + (yi + yi1) * A_temp;  
end  

A = A / 2; % 最终面积取绝对值  
Cx = Cx / (6 * A);  
Cy = Cy / (6 * A);  
  
end
  • 获取绘图区单位长度磅数函数
function unitLength = getUnitLength()
% 获取绘图区的每单位在屏幕上的长度(磅)
   
% 获取图形窗口的大小和位置  
Po = get(gcf, 'Position'); % 返回的单位是点 (points)，每个点约为 1/72 英寸  
figWidth = Po(3); % 图形的宽度 

% X轴范围  
xl = xlim;
rangeX = xl(2) - xl(1); 

% 绘图区的每单位在屏幕上的长度(磅)
unitLength = figWidth/rangeX;

end
  • 判断数组中所有元素是否同号函数
function flag = judgeSign(arr) 
% 判断数组中所有元素是否同号(包含0也算同号)

    % 计算数组每个元素的符号  
    signs = sign(arr(arr~=0));  
    
    % 获取唯一符号  
    uniqueSigns = unique(signs);  
    
    % 判断是否只有一个唯一符号，并且该符号不为零  
    if length(uniqueSigns) == 1 && uniqueSigns ~= 0  
        flag = true; % 同号  
    else  
        flag = false; % 不同号或包含零  
    end  
end

总结

  这只是一个基础的示例，实际中还会有更具体的、更细致的要求，这就需要再做额外调整；另外本人也仍在学习中，这只是个人的学习笔记，可能还有一些不足之处，欢迎指正。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2080834.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

RKNPU2从入门到实践 --- 【4】RKNN 模型构建【使用pycharm一步一步搭建RKNN模型】

RKNPU2从入门到实践 --- 【4】RKNN 模型构建【使用pycharm一步一步搭建RKNN模型】

目录 前言 1.1 RKNN 初始化及对象释放 1.1.1 概念介绍 1.1.2 实际演示 1.2 RKNN 模型配置 1.2.1 概念介绍 1.2.2 实际演示 1.3 模型加载 1.3.1 概念介绍 1.3.1.1 Caffe模型加载接口 1.3.1.2 TensorFlow模型加载接口 1.3.1.3 TensorFlowLite 模型加载接口 1.3.…
阅读更多...
debian12 - 修改SSH端口连接回包

debian12 - 修改SSH端口连接回包

文章目录 debian12 - 修改SSH端口连接回包概述笔记先猜猜回包是哪个程序回的去下载对应版本的openssh代码工程用telnet测试的效果todo 关于ssh状态为active(start)的原因END debian12 - 修改SSH端口连接回包 概述 和同学讨论问题。 他说&#xff0c;用telnet去连接SSH端口&am…
阅读更多...
数据仓库系列10：如何处理维度表中的变化类型?

数据仓库系列10：如何处理维度表中的变化类型?

想象一下,你正在管理一个电商平台的数据仓库。突然,你发现一个重要客户的地址发生了变化。这个简单的变更可能会对你的分析产生巨大影响。如何确保你的数据仓库能够准确地反映这种变化,同时又不丢失历史信息?欢迎来到数据仓库中最具挑战性的问题之一:维度表变化的处理。 目录…
阅读更多...
记录imbalanced_learn离线安装

记录imbalanced_learn离线安装

1 离线安装需要3个文件&#xff1a; 文件位置&#xff1a; ‘D:\非常重要\imbalanced-learn’ 2 复制到这个路径&#xff0c;即可 ‘…/miniconda3/lib/python3.8/site-packages’
阅读更多...
数据结构与算法——Java实现 1.初识算法 —— 二分查找

数据结构与算法——Java实现 1.初识算法 —— 二分查找

目录 一、线性查找 二、二分查找 基础版 问题1 —— 循环条件 问题2 —— ij/2有没有问题 问题3 —— 代码中都写成 < 有何好处 改动版 人生的意义就是要独自穿过悲喜 —— 24.8.27 需求:在有序数组A内&#xff0c;查找值 target&#xff0c;如果找到返回索引&#xff0c;如…
阅读更多...
小鹏在这次发布会上有哪些黑科技呢？

小鹏在这次发布会上有哪些黑科技呢？

在今晚举办的小鹏10年热爱之夜&小鹏MONA MO3上市发布会上&#xff0c;何小鹏宣布&#xff0c;小鹏自研图灵芯片已于8月23日流片成功。据介绍&#xff0c;小鹏图灵芯片是全球首颗同时应用在AI汽车、机器人、飞行汽车的AI芯片&#xff0c;为AI大模型定制。 该芯片采用40核心…
阅读更多...
【STM32】时钟体系

【STM32】时钟体系

一、时钟体系 为什么需要时钟&#xff1f; 时钟可以为系统提供精确的定时&#xff0c;比如时间显示&#xff0c;定时器&#xff0c;pwm… 为芯片各功能模块提供工作势能,使能各组管脚工作&#xff0c;如果不使能&#xff0c;管脚无法工作 同步数据传输 给单片机提供一个时…
阅读更多...
RabbitMQ中的死信交换机？（RabbitMQ延迟队列有了解过吗）

RabbitMQ中的死信交换机？（RabbitMQ延迟队列有了解过吗）

延迟队列 延迟队列:进入队列的消息会被延迟消费的队列。 延迟队列死信交换机 TTL&#xff08;过期时间&#xff09; 延迟队列的使用场景:超时订单、限时优惠、定时发布 死信交换机 当一个队列中的消息满足下列情况之一时&#xff0c;可以成为死信(dead letter): 消费者使…
阅读更多...
探讨Vision Pro的成本优化与设计改进之路

探讨Vision Pro的成本优化与设计改进之路

随着Apple Vision Pro的发布，这款革命性的头戴式显示设备凭借其创新技术和用户体验吸引了大量关注。然而，高昂的价格成为了一个不可忽视的问题，阻碍了它的普及。为了让更多消费者能够负担得起这款产品，Apple需要探索各种方法来降低成本而不牺牲用户体验。本文将总结一些关于…
阅读更多...
医用双目放大镜行业分析：前五大厂商占有大约39.0%的市场份额

医用双目放大镜行业分析：前五大厂商占有大约39.0%的市场份额

一、当前市场状况 1. 市场规模与增长趋势 - 目前医用双目放大镜市场呈现出稳定增长的态势。据报告显示&#xff0c;预计到 2030 年全球市场规模将达到 5.2 亿美元&#xff0c;年复合增长率为 7.8%&#xff0c;这表明该行业具有较大的发展潜力。 - 增长的动力主要来自医疗行业…
阅读更多...
排序算法（冒泡、插入、选择、快排、归并）原理动画及Python、Java实现

排序算法（冒泡、插入、选择、快排、归并）原理动画及Python、Java实现

排序算法&#xff08;冒泡、插入、选择、快排、归并&#xff09;原理动画及Python、Java实现 1 冒泡排序1.1 原理1.2 Python、Java实现 2 插入排序2.1 原理2.2 Python、Java实现 3 选择排序3.1 原理3.2 Python、Java实现 4 快速排序4.1 原理4.2 Python、Java实现 5 归并排序5.1…
阅读更多...
【机器学习】独立成分分析的基本概念、应用领域、具体实例（含python代码）以及ICA和PCA的联系和区别

【机器学习】独立成分分析的基本概念、应用领域、具体实例（含python代码）以及ICA和PCA的联系和区别

引言 独立成分分析&#xff08;Independent Component Analysis&#xff0c;简称ICA&#xff09;是一种统计方法&#xff0c;用于从多个观察到的混合信号中提取出原始的独立信号源 文章目录 引言一、独立成分分析1.1 定义1.2 独立成分分析的基本原理1.3 独立成分分析的步骤1.3.…
阅读更多...
RASA使用长文记录以及一些bug整理

RASA使用长文记录以及一些bug整理

RASA 学习笔记整理 一 安装 在虚拟环境中安装&#xff0c;进入python3版本的环境 conda activate python3 ai04机器旧版本&#xff1a;rasa-nlu和rasa-core是分开安装的 最新版本&#xff1a;rasa 将二者做了合并 直接安装 pip3 install rasa 在安装到如下步骤时候会报…
阅读更多...
读软件开发安全之道：概念、设计与实施11安全地编程

读软件开发安全之道：概念、设计与实施11安全地编程

1. 安全地编程 1.1. 在一个完整的软件设计过程中&#xff0c;我们要在创建和审查时就将安全性放在心中&#xff0c;但这只是产品开发过程的开始&#xff0c;接下来是实现、测试、部署、运行、监控、维护&#xff0c;并最终在生命周期结束时将其淘汰 1.2. 开发人员不仅必须忠实…
阅读更多...
Android Launcher启动过程

Android Launcher启动过程

## Launcher的启动流程&#xff1a; 1.Zygote进程 –> SystemServer进程 –> startOtherService方法 –> ActivityManagerService的systemReady方法 –> startHomeActivityLocked方法 –> ActivityStackSupervisor的startHomeActivity方法 –> 执行Activity…
阅读更多...
Java | Leetcode Java题解之第380题O(1)时间插入、删除和获取随机元素

Java | Leetcode Java题解之第380题O(1)时间插入、删除和获取随机元素

题目&#xff1a; 题解&#xff1a; class RandomizedSet {List<Integer> nums;Map<Integer, Integer> indices;Random random;public RandomizedSet() {nums new ArrayList<Integer>();indices new HashMap<Integer, Integer>();random new Rando…
阅读更多...
Java9模块化系统JPMS（Java Platform Module System）

Java9模块化系统JPMS（Java Platform Module System）

引言 随着Java技术的发展&#xff0c;开发人员面临的挑战之一是如何有效地管理和组织大型项目的依赖关系。传统的类路径&#xff08;classpath&#xff09;方法虽然简单&#xff0c;但在大型项目中却难以管理&#xff0c;尤其是在面对复杂的依赖关系时。为了解决这些问题&…
阅读更多...
Kafka入门：从零开始了解分布式流处理平台

Kafka入门：从零开始了解分布式流处理平台

什么是Kafka Apache Kafka是由LinkedIn公司开发&#xff0c;后来由Apache软件基金会维护的一个分布式、分区、多副本的基于ZooKeeper协调的分布式消息系统。Kafka不仅是一个消息队列&#xff0c;还是一个强大的流处理平台&#xff0c;它能够实时地处理大量数据&#xff0c;满足…
阅读更多...
Springboot如何实现redis消息的订阅发布

Springboot如何实现redis消息的订阅发布

1. 环境准备 确保你已经安装了 Redis 服务器&#xff0c;并且可以在本地或者远程访问它。如果你还没有安装 Redis&#xff0c;请先安装并启动 Redis 服务。 2. 创建 Spring Boot 项目 使用 Spring Initializr 或者其他 IDE 创建一个新的 Spring Boot 项目&#xff0c;并添加以下…
阅读更多...
Leetcode 1047-删除字符串中的所有相邻重复项

Leetcode 1047-删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S&#xff0c;重复项删除操作会选择两个相邻且相同的字母&#xff0c;并删除它们。 在 S 上反复执行重复项删除操作&#xff0c;直到无法继续删除。 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。 题解 题目链接 //先进后出&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023