Example: Bayesian Neural Network — NumPyro documentation

https://uvadlc-notebooks.readthedocs.io/en/latest/tutorial_notebooks/DL2/Bayesian_Neural_Networks/dl2_bnn_tut1_students_with_answers.html

注意，这些文档，也是有对应的版本的，左侧栏，的右下角，可以选择版本

（Sphinx — Sphinx documentation    Sphinx — Sphinx documentationhttps://www.sphinx-doc.org/生成的文档）

num.pyro.ai/en/stable/examples/bnn.html

docs.pyro.ai/en/stable/

未完待续

===========================================

项目简介
UVaDLC Notebooks是一个由Philipp（Phlippe）维护的开源项目，它包含了University of Virginia深度学习课程的全套Jupyter Notebook教程。这个项目不仅提供了丰富的理论知识，而且配套了实用的编程示例，让学习者能够更好地理解和应用深度学习技术。

技术分析
Jupyter Notebook
项目基于Jupyter Notebook，这是一种交互式计算环境，允许用户混合编写代码、文本和数学公式。这种格式便于理解复杂的算法，并提供了一种即时反馈的学习体验。

深度学习框架
教程涵盖了TensorFlow和PyTorch两种主流深度学习库，使学生可以灵活选择适合自己的工具进行学习和实践。

结构化课程内容
每个Notebook都按照课程章节组织，从基础知识到进阶主题，逐步引导学习者深入。这使得自学者可以根据自身的进度和需求自由选择学习路径。

应用场景
UVaDLC Notebooks非常适合以下用户：

初学者：希望入门深度学习并寻找结构化的学习资源。
研究人员：需要快速回顾某个特定概念或算法。
教师：在课堂上采用互动式的教学方式。
开发者：想要利用深度学习解决实际问题。
项目特点
实战导向：每个理论知识点都有配套的代码实现，鼓励动手实践。
实时更新：随着深度学习领域的快速发展，项目保持与最新技术和研究同步。
详尽解释：注释清晰，逻辑严谨，帮助理解复杂概念。
社区支持：通过GitHub，用户可以提交问题，贡献代码，共同进步。

• 使用Pyro的贝叶斯神经网络
• 在GitHub上编辑

---

教程1:使用Pyro的贝叶斯神经网络

填满的笔记本:-最新版本(V04/23):这款笔记本电脑

空笔记本:-最新版本(V04/23):​编辑

另请访问DL2教程Github回购和关联文档页面.

作者:伊尔泽·阿曼达·奥兹纳、伦纳德·贝雷斯卡、亚历山大·蒂曼斯和埃里克·纳利斯尼克

---

贝叶斯神经网络

贝叶斯神经网络是一种概率模型，它允许我们通过将网络的权重和偏差表示为概率分布而不是固定值来估计预测中的不确定性。这使我们能够整合先前的知识模型中的权重和偏差，以及更新我们的信念当我们观察数据时。

数学上，贝叶斯神经网络可以表示如下:

给定一组输入数据x，我们要预测相应的输出y。神经网络将这种关系表示为一个函数f(x,θ)，在哪里θ是网络的权重和偏差。在贝叶斯神经网络中，我们将权重和偏差表示为概率分布，因此f(x,θ)成为可能输出的概率分布:

p(y|x,D)=∫p(y|x,θ)p(θ|D)dθ

在哪里p(y|x,θ)是似然函数，它给出了观察的概率y考虑到x和θ，以及p(θ|D)是给定观察数据的权重和偏差的后验分布D.

为了进行预测，我们使用后验预测分布:

p(y∗|x∗,D)=∫p(y∗|x∗,θ)p(θ|D)dθ

在哪里x∗是一个新的输入y∗是相应的预测输出。

为了估计(难以处理的)后验分布p(θ|D)，我们可以使用马尔可夫链蒙特卡罗(MCMC)或变分推断(VI)。

模拟数据

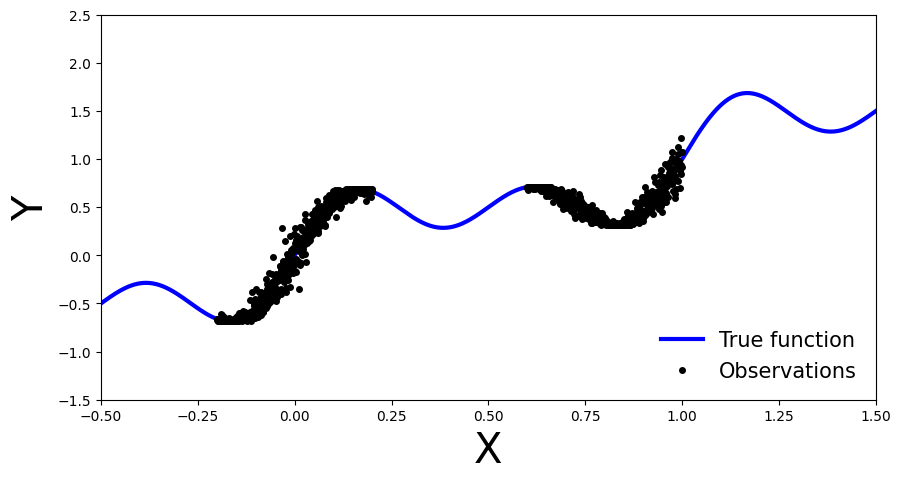
让我们从正弦函数中产生噪声观测值。

[3]:

import torch
import numpy as np
import matplotlib.pyplot as plt

# Set random seed for reproducibility
np.random.seed(42)

# Generate data
x_obs = np.hstack([np.linspace(-0.2, 0.2, 500), np.linspace(0.6, 1, 500)])
noise = 0.02 * np.random.randn(x_obs.shape[0])
y_obs = x_obs + 0.3 * np.sin(2 * np.pi * (x_obs + noise)) + 0.3 * np.sin(4 * np.pi * (x_obs + noise)) + noise

x_true = np.linspace(-0.5, 1.5, 1000)
y_true = x_true + 0.3 * np.sin(2 * np.pi * x_true) + 0.3 * np.sin(4 * np.pi * x_true)

# Set plot limits and labels
xlims = [-0.5, 1.5]
ylims = [-1.5, 2.5]

# Create plot
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x_true, y_true, 'b-', linewidth=3, label="True function")
ax.plot(x_obs, y_obs, 'ko', markersize=4, label="Observations")
ax.set_xlim(xlims)
ax.set_ylim(ylims)
ax.set_xlabel("X", fontsize=30)
ax.set_ylabel("Y", fontsize=30)
ax.legend(loc=4, fontsize=15, frameon=False)

plt.show()

Pyro入门

让我们现在安装Pyro。在此步骤之后，您可能需要重新启动运行时。

[4]:

!pip install pyro-ppl

Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: pyro-ppl in /usr/local/lib/python3.9/dist-packages (1.8.4)
Requirement already satisfied: numpy>=1.7 in /usr/local/lib/python3.9/dist-packages (from pyro-ppl) (1.22.4)
Requirement already satisfied: pyro-api>=0.1.1 in /usr/local/lib/python3.9/dist-packages (from pyro-ppl) (0.1.2)
Requirement already satisfied: opt-einsum>=2.3.2 in /usr/local/lib/python3.9/dist-packages (from pyro-ppl) (3.3.0)
Requirement already satisfied: torch>=1.11.0 in /usr/local/lib/python3.9/dist-packages (from pyro-ppl) (2.0.0+cu118)
Requirement already satisfied: tqdm>=4.36 in /usr/local/lib/python3.9/dist-packages (from pyro-ppl) (4.65.0)
Requirement already satisfied: networkx in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (3.1)
Requirement already satisfied: filelock in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (3.11.0)
Requirement already satisfied: sympy in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (1.11.1)
Requirement already satisfied: typing-extensions in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (4.5.0)
Requirement already satisfied: triton==2.0.0 in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (2.0.0)
Requirement already satisfied: jinja2 in /usr/local/lib/python3.9/dist-packages (from torch>=1.11.0->pyro-ppl) (3.1.2)
Requirement already satisfied: lit in /usr/local/lib/python3.9/dist-packages (from triton==2.0.0->torch>=1.11.0->pyro-ppl) (16.0.1)
Requirement already satisfied: cmake in /usr/local/lib/python3.9/dist-packages (from triton==2.0.0->torch>=1.11.0->pyro-ppl) (3.25.2)
Requirement already satisfied: MarkupSafe>=2.0 in /usr/local/lib/python3.9/dist-packages (from jinja2->torch>=1.11.0->pyro-ppl) (2.1.2)
Requirement already satisfied: mpmath>=0.19 in /usr/local/lib/python3.9/dist-packages (from sympy->torch>=1.11.0->pyro-ppl) (1.3.0)

具有高斯先验和似然的贝叶斯神经网络

我们的第一个贝叶斯神经网络对权重采用高斯先验，对数据采用高斯似然函数。该网络是具有一个隐藏层的浅层神经网络。

具体来说，我们在权重上使用以下先验θ:

p(θ)=N(0,10⋅I),在哪里I是单位矩阵。

为了训练网络，我们定义了一个似然函数，将网络的预测输出与实际数据点进行比较:

p(yi|xi,θ)=N(NNθ(xi),σ2)，有先验σ∼Γ(1,1).

这里，yi表示的实际输出i第个数据点，xi表示该数据点的输入，σ是正态分布的标准偏差参数NNθ浅层神经网络是否由参数化θ.

注意，我们使用σ2代替σ因为我们使用了高斯先验σ当执行变分推断时，希望避免标准差为负值。

[5]:

import pyro
import pyro.distributions as dist
from pyro.nn import PyroModule, PyroSample
import torch.nn as nn


class MyFirstBNN(PyroModule):
    def __init__(self, in_dim=1, out_dim=1, hid_dim=5, prior_scale=10.):
        super().__init__()

        self.activation = nn.Tanh()  # or nn.ReLU()
        self.layer1 = PyroModule[nn.Linear](in_dim, hid_dim)  # Input to hidden layer
        self.layer2 = PyroModule[nn.Linear](hid_dim, out_dim)  # Hidden to output layer

        # Set layer parameters as random variables
        self.layer1.weight = PyroSample(dist.Normal(0., prior_scale).expand([hid_dim, in_dim]).to_event(2))
        self.layer1.bias = PyroSample(dist.Normal(0., prior_scale).expand([hid_dim]).to_event(1))
        self.layer2.weight = PyroSample(dist.Normal(0., prior_scale).expand([out_dim, hid_dim]).to_event(2))
        self.layer2.bias = PyroSample(dist.Normal(0., prior_scale).expand([out_dim]).to_event(1))

    def forward(self, x, y=None):
        x = x.reshape(-1, 1)
        x = self.activation(self.layer1(x))
        mu = self.layer2(x).squeeze()
        sigma = pyro.sample("sigma", dist.Gamma(.5, 1))  # Infer the response noise

        # Sampling model
        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mu, sigma * sigma), obs=y)
        return mu

定义并运行马尔可夫链蒙特卡罗采样器

首先，我们可以使用MCMC来计算无偏估计关于p(y|x,D)=Eθ∼p(θ|D)[p(y|x,θ)]通过蒙特卡罗抽样。具体来说，我们可以近似Eθ∼p(θ|D)[p(y|x,θ)]如下所示:

Eθ∼p(θ|D)[p(y|x,θ)]≈1N∑i=1Np(y|x,θi),

在哪里θi∼p(θi|D)∝p(D|θ)p(θ)是从后验分布中抽取的样本。因为归一化常数是难以处理的，我们需要MCMC方法，如哈密尔顿蒙特卡罗，从非归一化后验样本中抽取样本。

在这里，我们使用不掉头(坚果)内核。

[6]:

from pyro.infer import MCMC, NUTS

model = MyFirstBNN()

# Set Pyro random seed
pyro.set_rng_seed(42)

# Define Hamiltonian Monte Carlo (HMC) kernel
# NUTS = "No-U-Turn Sampler" (https://arxiv.org/abs/1111.4246), gives HMC an adaptive step size
nuts_kernel = NUTS(model, jit_compile=False)  # jit_compile=True is faster but requires PyTorch 1.6+

# Define MCMC sampler, get 50 posterior samples
mcmc = MCMC(nuts_kernel, num_samples=50)

# Convert data to PyTorch tensors
x_train = torch.from_numpy(x_obs).float()
y_train = torch.from_numpy(y_obs).float()

# Run MCMC
mcmc.run(x_train, y_train)

Sample: 100%|██████████| 100/100 [04:57,  2.98s/it, step size=3.40e-04, acc. prob=0.959]

我们计算并绘制预测分布。

[7]:

from pyro.infer import Predictive

predictive = Predictive(model=model, posterior_samples=mcmc.get_samples())
x_test = torch.linspace(xlims[0], xlims[1], 3000)
preds = predictive(x_test)

[8]:

def plot_predictions(preds):
    y_pred = preds['obs'].T.detach().numpy().mean(axis=1)
    y_std = preds['obs'].T.detach().numpy().std(axis=1)

    fig, ax = plt.subplots(figsize=(10, 5))
    xlims = [-0.5, 1.5]
    ylims = [-1.5, 2.5]
    plt.xlim(xlims)
    plt.ylim(ylims)
    plt.xlabel("X", fontsize=30)
    plt.ylabel("Y", fontsize=30)

    ax.plot(x_true, y_true, 'b-', linewidth=3, label="true function")
    ax.plot(x_obs, y_obs, 'ko', markersize=4, label="observations")
    ax.plot(x_obs, y_obs, 'ko', markersize=3)
    ax.plot(x_test, y_pred, '-', linewidth=3, color="#408765", label="predictive mean")
    ax.fill_between(x_test, y_pred - 2 * y_std, y_pred + 2 * y_std, alpha=0.6, color='#86cfac', zorder=5)

    plt.legend(loc=4, fontsize=15, frameon=False)

[9]:

plot_predictions(preds)

练习1:深度贝叶斯神经网络

我们可以以类似的方式定义深度贝叶斯神经网络，在权重上具有高斯先验:

p(θ)=N(0,5⋅I).

似然函数也是高斯函数:

p(yi|xi,θ)=N(NNθ(xi),σ2)，与σ∼Γ(0.5,1).

实现深度贝叶斯神经网络并运行MCMC以获得后验样本。计算并绘制预测分布。使用以下网络架构:隐层数:5，每层隐单元数:10，激活函数:Tanh，先验尺度:5。

[10]:

class BNN(PyroModule):
    def __init__(self, in_dim=1, out_dim=1, hid_dim=10, n_hid_layers=5, prior_scale=5.):
        super().__init__()

        self.activation = nn.Tanh()  # could also be ReLU or LeakyReLU
        assert in_dim > 0 and out_dim > 0 and hid_dim > 0 and n_hid_layers > 0  # make sure the dimensions are valid

        # Define the layer sizes and the PyroModule layer list
        self.layer_sizes = [in_dim] + n_hid_layers * [hid_dim] + [out_dim]
        layer_list = [PyroModule[nn.Linear](self.layer_sizes[idx - 1], self.layer_sizes[idx]) for idx in
                      range(1, len(self.layer_sizes))]
        self.layers = PyroModule[torch.nn.ModuleList](layer_list)

        for layer_idx, layer in enumerate(self.layers):
            layer.weight = PyroSample(dist.Normal(0., prior_scale * np.sqrt(2 / self.layer_sizes[layer_idx])).expand(
                [self.layer_sizes[layer_idx + 1], self.layer_sizes[layer_idx]]).to_event(2))
            layer.bias = PyroSample(dist.Normal(0., prior_scale).expand([self.layer_sizes[layer_idx + 1]]).to_event(1))

    def forward(self, x, y=None):
        x = x.reshape(-1, 1)
        x = self.activation(self.layers[0](x))  # input --> hidden
        for layer in self.layers[1:-1]:
            x = self.activation(layer(x))  # hidden --> hidden
        mu = self.layers[-1](x).squeeze()  # hidden --> output
        sigma = pyro.sample("sigma", dist.Gamma(.5, 1))  # infer the response noise

        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mu, sigma * sigma), obs=y)
        return mu

用MCMC训练深BNN…

[11]:

# define model and data
model = BNN(hid_dim=10, n_hid_layers=5, prior_scale=5.)

# define MCMC sampler
nuts_kernel = NUTS(model, jit_compile=False)
mcmc = MCMC(nuts_kernel, num_samples=50)
mcmc.run(x_train, y_train)

Sample: 100%|██████████| 100/100 [12:04,  7.24s/it, step size=6.85e-04, acc. prob=0.960]

计算预测分布…

[12]:

predictive = Predictive(model=model, posterior_samples=mcmc.get_samples())
preds = predictive(x_test)
plot_predictions(preds)

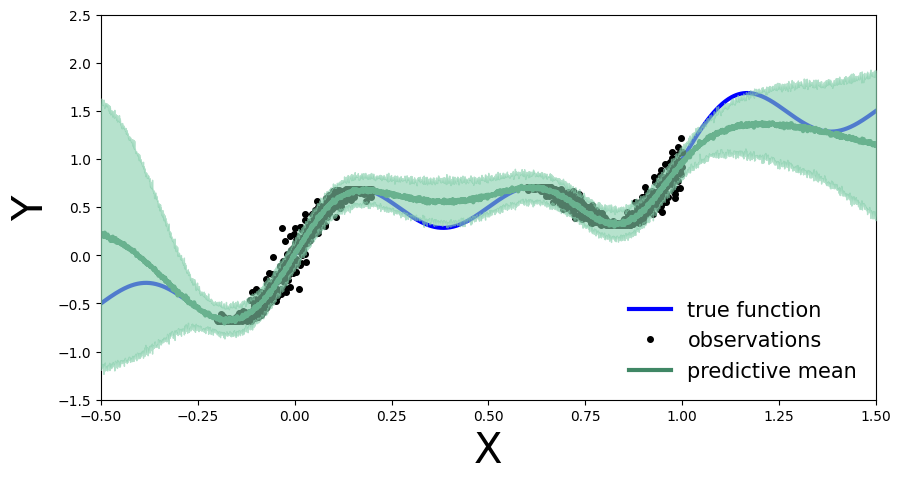
用平均场变分推理训练贝叶斯网络

我们现在将转向变分推理。因为归一化后验概率密度p(θ|D)是难以处理的，我们用一个易处理的参数化密度来近似它qϕ(θ)在概率密度家族中Q。变化的参数表示为ϕ而变化的密度在Pyro中被称为“导子”。目标是通过最小化KL散度找到最接近后验概率的变分概率密度

KL(qϕ(θ)||p(θ|D))

关于变分参数。然而，直接最小化KL散度是不容易处理的，因为我们假设后验密度是难以处理的。为了解决这个问题，我们使用贝叶斯定理来获得

原木⁡p(D|θ)=KL(qϕ(θ)||p(θ|D))+ELBO(qϕ(θ)),

在哪里ELBO(qϕ(θ))是证据下限，由提供

ELBO(qϕ(θ))=Eθ∼qϕ(θ)[原木⁡p(y|x,θ)]−KL(qϕ(θ)||p(θ)).

通过最大化ELBO，我们间接地最小化变分概率密度和后验密度之间的KL散度。

变密度随机变分推理的建立qϕ(θ)通过使用带有对角协方差矩阵的正态概率密度:

[13]:

from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import AutoDiagonalNormal
from tqdm.auto import trange
pyro.clear_param_store()

model = BNN(hid_dim=10, n_hid_layers=5, prior_scale=5.)
mean_field_guide = AutoDiagonalNormal(model)
optimizer = pyro.optim.Adam({"lr": 0.01})

svi = SVI(model, mean_field_guide, optimizer, loss=Trace_ELBO())
pyro.clear_param_store()

num_epochs = 25000
progress_bar = trange(num_epochs)

for epoch in progress_bar:
    loss = svi.step(x_train, y_train)
    progress_bar.set_postfix(loss=f"{loss / x_train.shape[0]:.3f}")

如前所述，我们从训练的变化密度计算预测分布抽样。

[14]:

predictive = Predictive(model, guide=mean_field_guide, num_samples=500)
preds = predictive(x_test)
plot_predictions(preds)

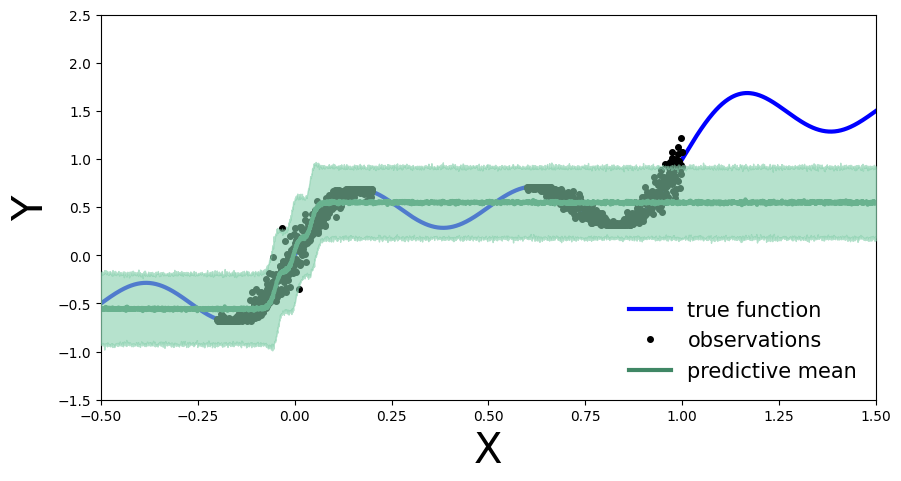
练习2:使用变分推理的贝叶斯更新

如果我们获得新的数据点，表示为D′，在使用观察值执行变分推断之后D?

[15]:

# Generate new observations
x_new = np.linspace(0.2, 0.6, 100)
noise = 0.02 * np.random.randn(x_new.shape[0])
y_new = x_new + 0.3 * np.sin(2 * np.pi * (x_new + noise)) + 0.3 * np.sin(4 * np.pi * (x_new + noise)) + noise

# Generate true function
x_true = np.linspace(-0.5, 1.5, 1000)
y_true = x_true + 0.3 * np.sin(2 * np.pi * x_true) + 0.3 * np.sin(4 * np.pi * x_true)

# Set axis limits and labels
plt.xlim(xlims)
plt.ylim(ylims)
plt.xlabel("X", fontsize=30)
plt.ylabel("Y", fontsize=30)

# Plot all datasets
plt.plot(x_true, y_true, 'b-', linewidth=3, label="True function")
plt.plot(x_new, y_new, 'ko', markersize=4, label="New observations", c="r")
plt.plot(x_obs, y_obs, 'ko', markersize=4, label="Old observations")
plt.legend(loc=4, fontsize=15, frameon=False)
plt.show()

<ipython-input-15-68b431b95167>:18: UserWarning: color is redundantly defined by the 'color' keyword argument and the fmt string "ko" (-> color='k'). The keyword argument will take precedence.
  plt.plot(x_new, y_new, 'ko', markersize=4, label="New observations", c="r")

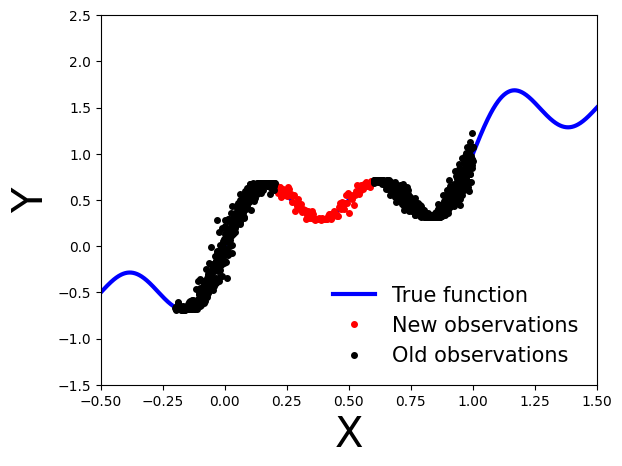
贝叶斯更新

当新的观察变得可用时，我们如何使用变分推理对模型执行贝叶斯更新？

我们可以使用先前计算的后验概率密度作为新的先验，并用新的观测值更新后验概率密度。具体地，更新后的后验概率密度由下式给出:

p(θ|D′)=p(D′|θ)qϕ(θ)∫p(D′|θ)qϕ(θ)

请注意，我们希望仅使用新的观察来更新我们的模型D′依赖于这样的事实，即用作我们的新先验的变分密度携带了关于旧观测的必要信息D.

在Pyro中实现

为了在Pyro中实现这一点，我们可以从guide并且使用它们来初始化新模型中的先验，该新模型类似于用于变分推断的原始模型。

从高斯guide我们可以将变分参数(平均值和标准偏差)提取为:

mu = guide.get_posterior().mean
sigma = guide.get_posterior().stddev

练习2.1学习旧观察的模型

首先，如前所述，我们使用高斯先验定义一个模型N(0,10⋅I).

训练模特MyFirstBNN根据旧的观察D使用变分推理AutoDiagonalNormal()作为向导。

[16]:

from pyro.optim import Adam
pyro.set_rng_seed(42)
pyro.clear_param_store()

model = MyFirstBNN()
guide = AutoDiagonalNormal(model)
optim = Adam({"lr": 0.03})
svi = pyro.infer.SVI(model, guide, optim, loss=Trace_ELBO())

num_iterations = 10000
progress_bar = trange(num_iterations)

for j in progress_bar:
    loss = svi.step(x_train, y_train)
    progress_bar.set_description("[iteration %04d] loss: %.4f" % (j + 1, loss / len(x_train)))

[17]:

predictive = Predictive(model, guide=guide, num_samples=5000)
preds = predictive(x_test)
plot_predictions(preds)

接下来，我们可以从中提取变分参数(均值和标准差)guide并且使用它们来初始化新模型中的先验，该新模型类似于用于变分推断的原始模型。

[18]:

# Extract variational parameters from guide
mu = guide.get_posterior().mean.detach()
stddev = guide.get_posterior().stddev.detach()

[19]:

for name, value in pyro.get_param_store().items():
    print(name, pyro.param(name))

AutoDiagonalNormal.loc Parameter containing:
tensor([ 4.4192,  2.0755,  2.5186,  2.9757, -2.8465, -4.5504, -0.6823,  8.6747,
         8.4490,  1.4790,  1.2583,  5.1179,  0.9285, -1.8939,  4.3386,  1.2919,
        -1.0739], requires_grad=True)
AutoDiagonalNormal.scale tensor([1.4528e-02, 2.4028e-03, 2.1688e+00, 1.6080e+00, 4.6767e-03, 1.4400e-02,
        1.4626e-03, 1.5972e+00, 8.8795e-01, 2.9016e-03, 6.1736e-03, 9.5345e-03,
        6.3799e-03, 5.4558e-03, 7.9139e-03, 5.9700e-03, 4.8264e-02],
       grad_fn=<SoftplusBackward0>)

练习2.2用变化的参数初始化第二个模型

定义一个新模型，类似于MyFirstBNN(PyroModule)，它采用变分参数并使用它们来初始化先验。

[20]:

class UpdatedBNN(PyroModule):
    def __init__(self, mu, stddev, in_dim=1, out_dim=1, hid_dim=5):
        super().__init__()
        self.mu = mu
        self.stddev = stddev

        self.activation = nn.Tanh()
        self.layer1 = PyroModule[nn.Linear](in_dim, hid_dim)
        self.layer2 = PyroModule[nn.Linear](hid_dim, out_dim)

        self.layer1.weight = PyroSample(dist.Normal(self.mu[0:5].unsqueeze(1), self.stddev[0:5].unsqueeze(1)).to_event(2))
        self.layer1.bias = PyroSample(dist.Normal(self.mu[5:10], self.stddev[5:10]).to_event(1))
        self.layer2.weight = PyroSample(dist.Normal(self.mu[10:15].unsqueeze(0), self.stddev[10:15].unsqueeze(0)).to_event(2))
        self.layer2.bias = PyroSample(dist.Normal(self.mu[15:16], self.stddev[15:16]).to_event(1))
        # 17th parameter is parameter sigma from the Gamma distribution

    def forward(self, x, y=None):
        x = x.reshape(-1, 1)
        x = self.activation(self.layer1(x))
        mu = self.layer2(x).squeeze()
        sigma = pyro.sample("sigma", dist.Gamma(.5, 1))

        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mu, sigma * sigma), obs=y)
        return mu

练习2.3对新模型进行变分推理

然后使用新的观察值对这个新模型进行变分推断，并绘制预测分布图。你观察到了什么？预测分布与练习2.1中获得的分布相比如何？

[21]:

x_train_new = torch.from_numpy(x_new).float()
y_train_new = torch.from_numpy(y_new).float()

pyro.clear_param_store()
new_model = UpdatedBNN(mu, stddev)
new_guide = AutoDiagonalNormal(new_model)
optim = Adam({"lr": 0.01})
svi = pyro.infer.SVI(new_model, new_guide, optim, loss=Trace_ELBO())

num_iterations = 1000
progress_bar = trange(num_iterations)

for j in progress_bar:
    loss = svi.step(x_train_new, y_train_new)
    progress_bar.set_description("[iteration %04d] loss: %.4f" % (j + 1, loss / len(x_train)))

[22]:

predictive = Predictive(new_model, guide=new_guide, num_samples=5000)
preds = predictive(x_test)
plot_predictions(preds)

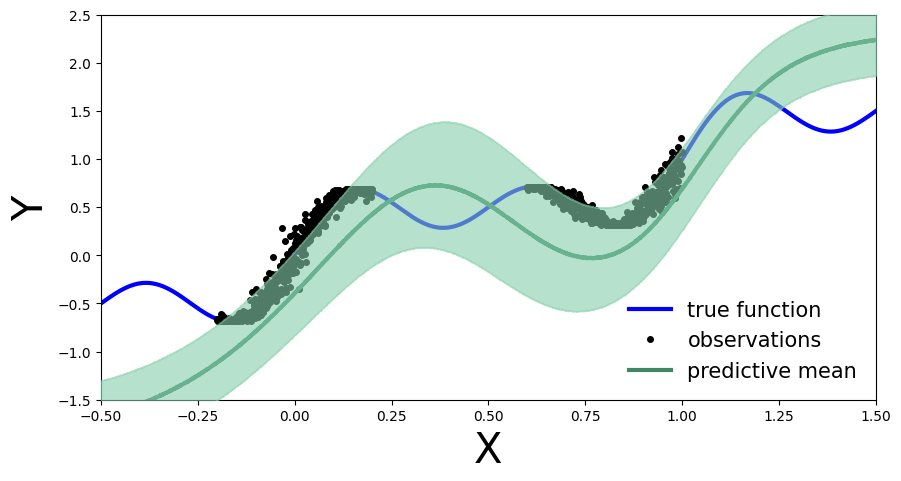
然后以前的