备战秋招60天算法挑战，Day25

news2024/11/17 15:34:20

题目链接： https://leetcode.cn/problems/combination-sum/

视频题解： https://www.bilibili.com/video/BV1xyiueHEb4/

LeetCode 39. 组合总和

题目描述

给你一个无重复元素的整数数组candidates和一个目标整数target，找出candidates中可以使数字和为目标数target的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为target的不同组合数少于150个。

举个例子：

输入： candidates = [2,3,6,7], target = 7
输出： [[2,2,3],[7]]
解释：
2和3可以形成一组候选，2 + 2 + 3 = 7。注意2可以使用多次。
7也是一个候选，7 = 7。
仅有这两种组合。

视频题解

组合总和

思路来源

知识回顾

回溯是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解组合问题、排列问题等。回溯的核心思想是通过自上而下递归的方式枚举所有可能的解，直到找到符合条件的解为止。回溯算法通常使用递归函数来实现，每次递归时都会对当前状态进行判断，如果符合条件则继续递归，否则回溯到上一层状态。

思路解析

本题是组合问题需要枚举所有可能的解，可以用回溯法来解，回溯的关键在于划分子问题和确定回溯条件。

下图是target = 7， candidates = [2, 3, 7]，自上而下枚举所有可能解的过程，叶子节点为0，说明找到一个符合条件的解，其解就是由根节点到叶子节点之间树枝上的数组成。比如[2, 2, 3]，[2, 3, 2]，[3, 2, 2]，[7]都是符合条件的解。

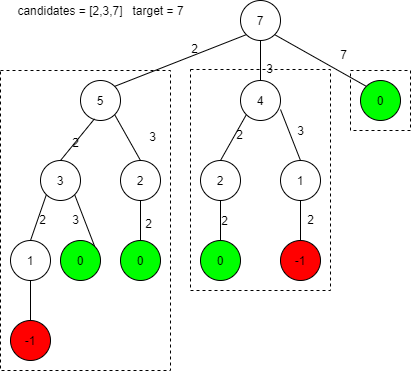
从上面的例子可以看出对于target = 7的情况可以划分为求target = 5，target = 4，target = 0三个子问题，这样就明确了子问题的划分： 对于target = n，我们可以划分成target = n - candidates[0]，...，target = n - candidates[m-1]，m个子问题，其中m为candidates的长度。

接下来就是确定回溯条件，很明显本题的回溯条件是叶子节点为0或为负数。

到这里回溯的两个关键问题都已经明确了，细心的同学应该已经看到对于上面的例子推导出了重复的解，[2, 2, 3]，[2, 3, 2]，[3, 2, 2]这三个解是重复的，这个时候就需要剪枝来剪掉重复的解。要如何剪枝呢，其实只需要在推导值为n - candidates[i]节点的子节点时，令target = n - candidates[i] - candidates[j]，i <= j < m就可以将重复的解给剪掉。

有些同学对剪枝这部分有点疑惑，还是用上面的例子，target = 7，零钱的集合为candidates=[2, 3, 7]。我们可以选择三个2、两个2、一个2、零个2，四种情况。我们把所有包含2的情况一次性选完，然后再从除去2以后的集合[3, 7]去做选择。这样就避免了重复解，如果还是有疑惑可以在纸上画一画，可以更直观的去理解。

C++代码

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> res;
        vector<int> temp;
        help(candidates, target, 0, res, temp);
        return res;
    }

    void help(vector<int>& candidates, int target, int start, vector<vector<int>>& res, vector<int>& temp) {
        //回溯条件
        if (target == 0) {
            //找到符合条件的解，保存起来
            res.push_back(temp);
            //开始回溯
            return;
        }
        //回溯条件
        if (target < 0) {
            //开始回溯
            return;
        }

        int candidates_len = candidates.size();
        //i=start是剪枝操作，如果i=0会存在重复解。
        for (int i = start; i < candidates_len; ++i) {
            if (target - candidates[i] >= 0) {
                temp.push_back(candidates[i]);
                //子问题
                help(candidates, target - candidates[i], i, res, temp);
                //回到上一个状态
                temp.pop_back();  
            }
        }

    }
};

java代码

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> temp = new ArrayList<>();
        help(candidates, target, 0, res, temp);
        return res;
    }
      private void help(int[] candidates, int target, int start, List<List<Integer>> res, List<Integer> temp) {
        // 回溯条件
        if (target == 0) {
            // 找到符合条件的解，保存起来
            res.add(new ArrayList<>(temp));
            // 开始回溯
            return;
        }
        // 回溯条件
        if (target < 0) {
            // 开始回溯
            return;
        }

        int candidates_len = candidates.length;
        // i=start是剪枝操作，如果i=0会存在重复解。
        for (int i = start; i < candidates_len; ++i) {
            if (target - candidates[i] >= 0) {
                temp.add(candidates[i]);
                // 子问题
                help(candidates, target - candidates[i], i, res, temp);
                // 回到上一个状态
                temp.remove(temp.size() - 1);
            }
        }
    }

}

python代码

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        res = []
        temp = []
        self.help(candidates, target, 0, res, temp)
        return res

    def help(self, candidates, target, start, res, temp):
        # 回溯条件
        if target == 0:
            # 找到符合条件的解，保存起来
            res.append(list(temp))
            # 开始回溯
            return
        # 回溯条件
        if target < 0:
            # 开始回溯
            return

        candidates_len = len(candidates)
        # i=start是剪枝操作，如果i=0会存在重复解。
        for i in range(start, candidates_len):
            if target - candidates[i] >= 0:
                temp.append(candidates[i])
                # 子问题
                self.help(candidates, target - candidates[i], i, res, temp)
                # 回到上一个状态
                temp.pop()