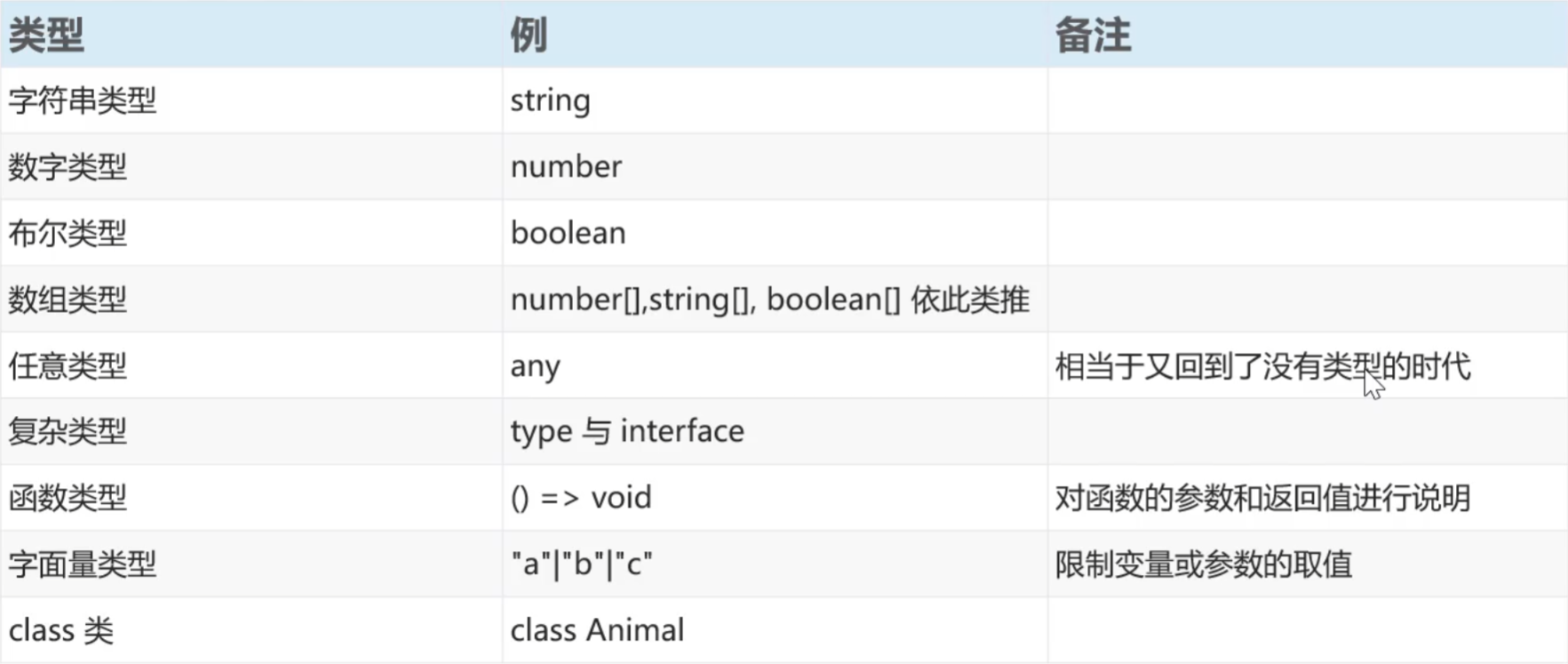
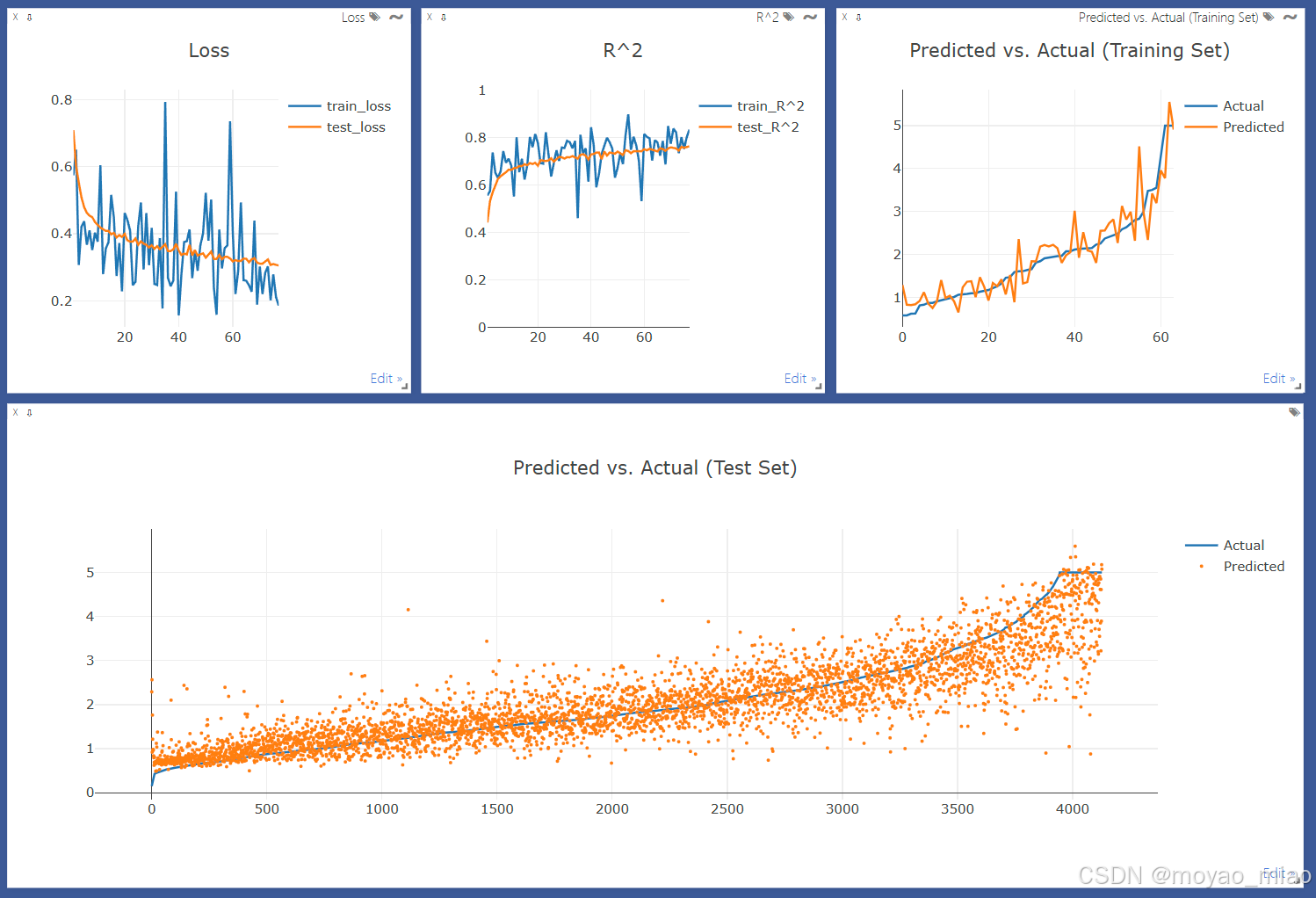
一、Held-Harp模型
海尔德和卡尔普在1970年提出景点模型,用于求解TSP问题的最优解下界·

该模型同样可以用于DCVRP问题,既有定理1成立。
定理1:根据Held-Karp模型使用向量 π = ( 0 , π 1 , π 2 , ⋯ , π n ) \pi=(0,\pi_1,\pi_2,\cdots,\pi_n) π=(0,π1,π2,⋯,πn)改造DCVRP问题中1个配送中心和n个顾客之间形成的(n+1)阶距离矩阵,不会改变DCVRP问题的最优解。
❓ 那么DCVRP-GR算法根据改造前后的距离矩阵进行求解,能够得到一致的求解结果吗?
案例说明,Held-Karp模型不会改变 DCVRP问题的最优解,但会改变DCVRP-GR的求解结果,这是因为 Held-Karp模型会改变距离矩阵中元素的大小次序关系。由此可知,在Held-Karp模型中采用不同的向量 π \pi π将会得到不同的改造后距离矩阵,从而DCVRP-GR算法的求解结果也会不同.
❓向量 π \pi π与DCVRP-GR算法的求解质量是否存在某种关联?

二、距离矩阵方差最小化方法
以向量 π \pi π做自变量,用该向量按照Held-Karp模型改造后的距离矩阵的方差为目标函数,尝试证明该目标函数存在极小值,结果发现该函数确实存在较小值,从而找到了一个最小化距离矩阵方差的方法。
2.1 证明存在性
目标函数


(3.10)改写为(3.16)

❓问题: 方差 σ ′ 2 \sigma'^2 σ′2看做n个变量( π 1 , π 2 , ⋯ , π n \pi_1,\pi_2,\cdots,\pi_n π1,π