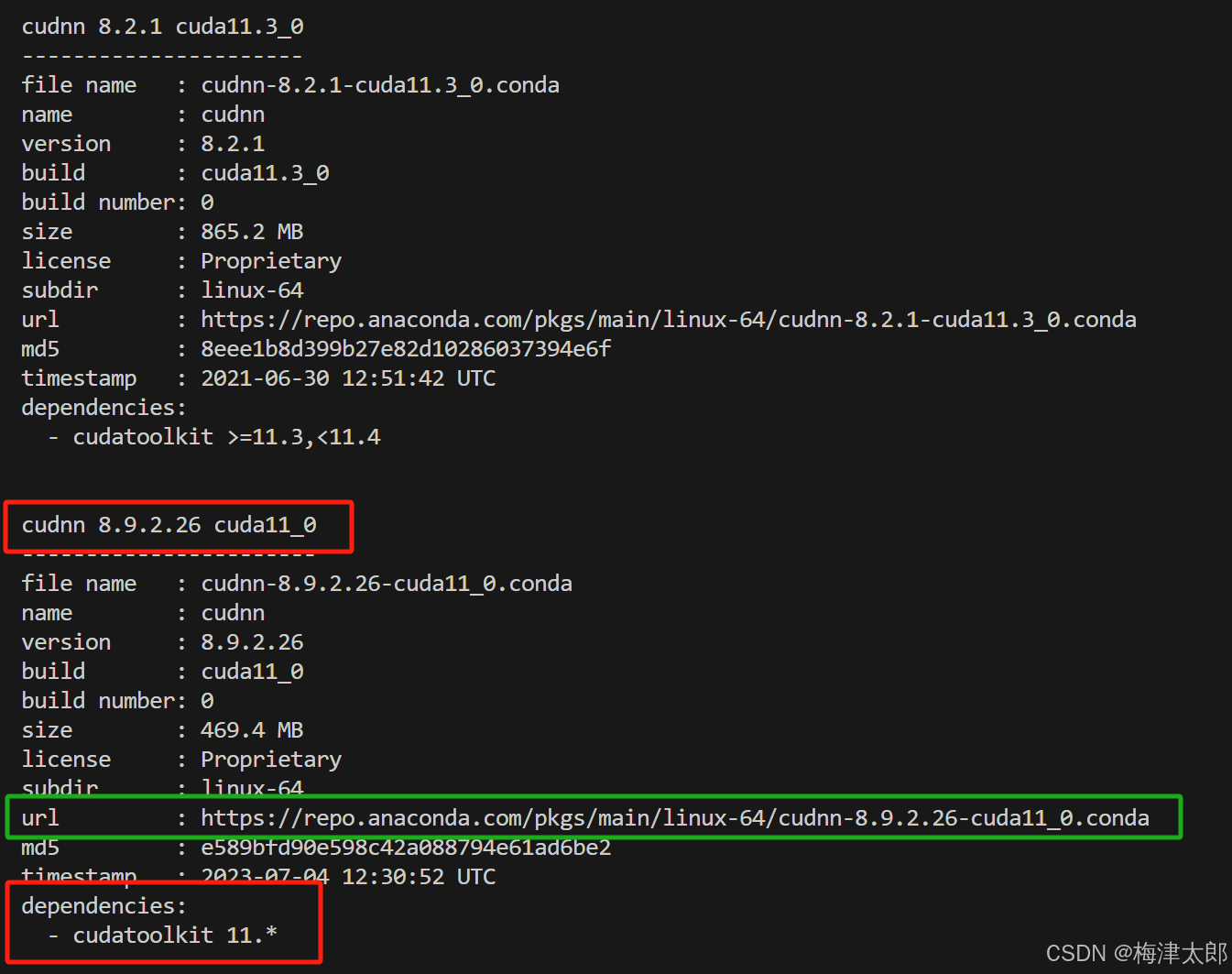
原文链接

KL散度是D(P||Q)，P和Q谁在前谁在后是有讲究的，P在前，就从P采样。
$$D_{KL}(P||Q)=E_{x-p(x)}(log(P(x)/Q(x)))$$想象一下，如果某个x的Q=0，1>P>0，则$D_{KL}$会直指∞。所以你要在这个KL形式下最小化KL，就必须遵循一个原则：P大，Q就得大，不然KL会很大。

反之，对于$D_{KL}(Q||P)$也是这个情况，Q大，P就得大。可是P是真实数据，是固定的，所以Q就得让自己大的地方正好是P大的地方。

理想情况下，这两种都能训练成功，但是训练往往是次优的。由于原则的差别，会让Q拟合P时产生两种截然不同的反应：mean-seeking和mode-seeking。
前者形容$D_{KL}(P||Q)$，后者形容$D_{KL}(Q||P)$。
看图更容易理解：红色是Q，蓝色是P。

这是$D_{KL}(P||Q)$的次优训练结果。刚才说了，Q大P小无所谓，但是P大Q就得大，因此Q在本身分布假设简单的情况下(例如是正态分布)，就只能获得这样的拟合。
这是$D_{KL}(Q||P)$的次优训练结果。刚才说了，P大Q小无所谓，但是Q大P就得大，因此Q在本身分布假设简单的情况下(例如是正态分布)，能力有限，就只能拟合P的一个高峰。

对于两种KL，$D_{KL}(P||Q)$叫forward KL，$D_{KL}(Q||P)$叫reverse KL。前者需要你采样P，后者需要你计算p(x)。

mean-seeking准备工作

在解释sft是mean-seeking，rl是mode-seeking前，对KL做个变形:

sft是mean-seeking

对于forward KL，简单把log打开就是第一个式子，H是P的熵。然后训练目标是改变策略，让forward KL最小。简化到最后就是上面那样。显然，要是停在argmin那块(倒数第二行)，这就是个P和Q的cross entropy，这就已经能联想到sft的目标函数了，这俩是一回事。

mode-seeking准备工作

reverse KL的拆解就不贴了。总之优化目标是这个。
如果我设置

即reward就是从偏好数据集分布来的，这样不犯忌讳，我偏好的肯定概率高，我偏好的肯定reward大，那我就直接拿概率当reward。log是递增函数，所以不影响上述规律。我这么一设置，reverse KL的优化目标就变成了:

这是最大熵强化学习的目标函数。要后面的-log最大，就得01分布，0去拿到∞，1拿到0。1放在reward最大的action上还能让目标函数更大。这是该目标函数工作的原理。
论证完毕。