VTK随笔四：VTK基本数据结构

news2024/11/24 6:35:55

一、可视化数据的基本特点

  • 离散性：为了让计算机能够获取、处理和分析数据，必须对无限、连续的空间体进行采样，生成有限的采样数据点，这些数据以离散点的形式存储，采样的过程是一个离散化的过程。
  • 数据具有规则或不规则的结构（结构化与非结构化）：可视化数据可以分为规则(Regular)和不规则(Irreguar)或者说结构化(Structured)和非结构化(Unstructured)。规则结构数据点之间有固定的关联关系，可以通过这些关联确定每个点的坐标，不规则结构数据之间没有固定的关联关系。
  • 数据具有维度：可视化数据具有零维、一维、二维、三维等任意维度

二、数据对象和数据集 

1、vtkDataObject

        在 VTK 中，数据一般以数据对象(Data Object，类 vtkDataObject)的形式表现，这是VTK 里可视化数据最常用的表达形式。 

 

2、vtkDataSet

        VTK里与数据集对应的类是vtkDataSet，该类从vtkDataObject直接派生。

vtkDataSet的组织结构由拓扑结构(Topology)和几何结构(Geometry)两部分组成。拓扑结构描述了对象的构成形式，几何结构描述了对象的空间位置关系。

        比如，想要在屏幕上显示一个三角形，首先必须定义三角形三个点的坐标(即Point Data，记三个点为P1、P2和P3)，然后将这三个点按照一定的顺序连接起来(P1-P2-P3，或者是P3-P2-P1的顺序)，这三个点定义了数据集的几何结构，它们的连接就构成了数据集的拓扑结构，亦即点数据定义了数据集的几何结构，单元数据定义数据集的拓扑结构，要形成完整的数据集，必须有几何和拓扑两种结构。

        拓扑结构具有几何变换不变性（旋转、平移和放缩），属性数据是对拓扑结构和几何结构信息的补充，属性数据可以是某个空间点的温度值，也可以是某个单元的质量等。

 

 示例代码：

	//创建三个坐标点
	vtkSmartPointer<vtkPoints> points = vtkSmartPointer<vtkPoints>::New();
	points->InsertNextPoint ( 1.0, 0.0, 0.0 ); //返回第一个点的ID：0
	points->InsertNextPoint ( 0.0, 0.0, 1.0 ); //返回第二个点的ID：1
	points->InsertNextPoint ( 0.0, 0.0, 0.0 ); //返回第三个点的ID：2

	//每两个坐标点之间分别创建一条线
	//SetId()的第一个参数是线段的端点ID，第二个参数是连接的点的ID
	vtkSmartPointer<vtkLine> line0 = vtkSmartPointer<vtkLine>::New();
	line0->GetPointIds()->SetId ( 0,0 ); 
	line0->GetPointIds()->SetId ( 1,1 );

	vtkSmartPointer<vtkLine> line1 = vtkSmartPointer<vtkLine>::New();
	line1->GetPointIds()->SetId ( 0,1 );
	line1->GetPointIds()->SetId ( 1,2 );

	vtkSmartPointer<vtkLine> line2 = vtkSmartPointer<vtkLine>::New();
	line2->GetPointIds()->SetId ( 0,2 );
	line2->GetPointIds()->SetId ( 1,0 );

	//创建Cell数组，用于存储以上创建的线段
	vtkSmartPointer<vtkCellArray> lines = vtkSmartPointer<vtkCellArray>::New();
	lines->InsertNextCell ( line0 );
	lines->InsertNextCell ( line1 );
	lines->InsertNextCell ( line2 );

	vtkSmartPointer<vtkPolyData> polydata = vtkSmartPointer<vtkPolyData>::New();

	//将点和线加入到数据集中，前者指定数据集的几何，后者指定其拓扑
	polydata->SetPoints ( points );
	polydata->SetLines ( lines );

	vtkSmartPointer<vtkPolyDataWriter> writer = vtkSmartPointer<vtkPolyDataWriter>::New();
	writer->SetFileName ( "TriangleLines.vtk" );
	writer->SetInputData ( polydata );
	writer->Write();

 三、单元类型

        数据集由一个或多个单元组成。一系列有序的点按指定类型连接所定义的结构就是单元(Cell)，单元是VTK可视化系统的基础。

1、线性单元
类型图示说明
VTK_VERTEX

image

顶点，由一个点定义，是零维的基本类型
VTK_POLY_VERTEX

image

多顶点，多个顶点组合而成，是零维的组合单元，其定义不受顶点顺序的限制
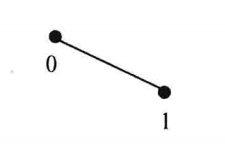
VTK_LINE

image

直线，一维的基本类型，由两个点定义，方向是从第一个点指向第二个点
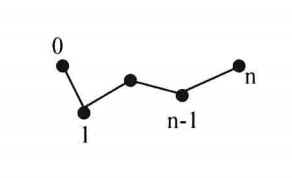
VTK_POLY_LINE

image

折线，由一个或多个线段组合成，一维的类型。由n+1个有序的点连接定义的，n表示折线的线段条数，每两个点(i, i+1)定义一条线段
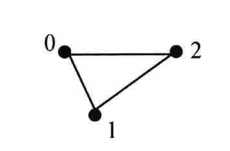
VTK_TRIANGLE

image

三角形，二维的基本类型，由三个点按逆时针的方向连接定义，点的连接方向和表面法向量符合右手法则
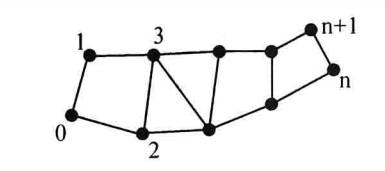
VTK_TRIANGLE_STRIP

image

三角形条带，由一个或多个三角形组合而成，二维类型。由n+2个有序的点连接定义的，n表示三角形条带里三角形的个数，定义三角形条带的点不需要共面。
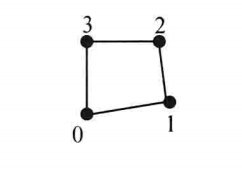
VTK_QUAD

image

四边形，二维的基本类型，是由共面的四个点按逆时针的方向连接定义的。四边形要求是非自交的凸多边形，利用右手法则可以得到改四边形的表面法向量
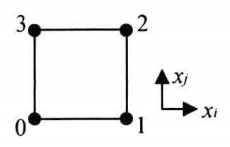
VTK_PIXEL

image

二维的基本类型，是由共面的四个点按一定的顺序连接定义的。该类型的单元与四边形的区别在拓扑结构上，Pixel类型要求相邻的两条边必须垂直，而且相对的两条边要与坐标轴平行，因此Pixel的表面法向量也与其中的一条坐标轴平行。定义Pixel的四个顶点的顺序与四边形不同，Pixel顶点的计数是先沿着X轴的方向，然后是Y轴，最后是Z轴方向。Pixel是四边形类型的特殊形式，注：Pixel是一种单元类型，与图像像素(Pixel)的概念不同
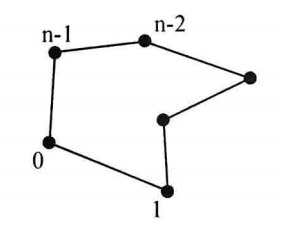
VTK_POLYGON

image

多边形，二维的基本类型，是由共面的三个或三个以上的点按逆时针方向的顺序连接定义的，多边形的表面法向量方向由右手法则确定。该类型要求多边形可以是非凸的，但是不能含有内部循环或者出现相交的边。多边形有n条边，n就是组成多边形的点的个数。
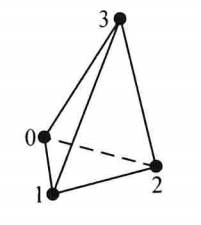
VTK_TETRA

image

四面体，三维的基本类型，是由不共面的四个点两两连接定义的，四面体有6条边4个面
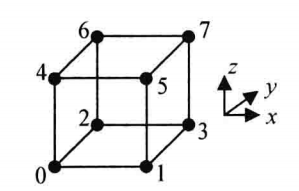
VTK_HEXAHEDRON

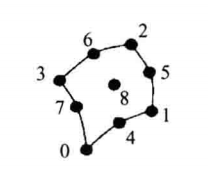
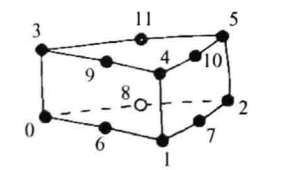
image

六面体，三维的基本类型，包含六个四边形表面、12条边和8个顶点，顶点连接顺序如图，六面体要求必须是凸的
VTK_VOXEL

image

三维的基本类型，与六面体的拓扑不一样，但几何上有所区别。Voxel要求相邻的两个面必须垂直，点的连接顺序如图。Voxel是六面体的特殊形式。与Pixel类似，Voxel与三维图像体素的概念是不同的
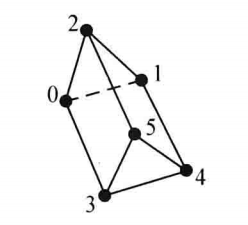
VTK_WEDGE

image

楔形，三维的基本类型，由3个四边形面、2个三角形面、9条边和6个顶点构成。六个点的连接顺序如图，要求面和边不能与其他的相交，且楔形必须是凸的
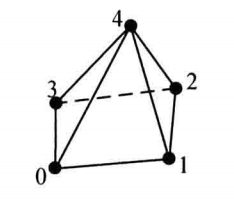
VTK_PYRAMID

image

角锥体，三维基本类型，由1个四边形面、4个三角形面、8条边和5个顶点构成。构成角锥体的点的连接顺序如图。定义四边形的点要求是共面的，且四个点构成的四边形必须是凸的，第五个点与其他四个点不在一个面上
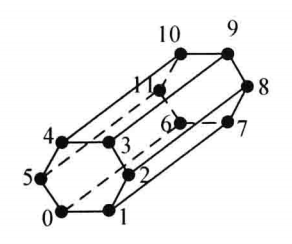
VTK_PENTAGONAL_PRISM

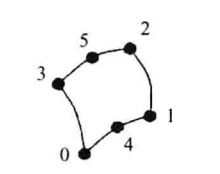
image

五棱柱，三维基本类型，由五个四边形面、两个五边形面、15条边和10个顶点构成。点的连接顺序如图，五棱柱的面和边不能与其他的相交且五棱柱必须是凸的
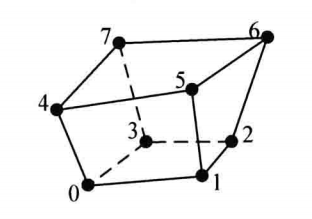
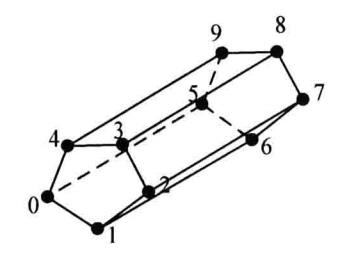
VTK_HEXAGONAL_PRISM

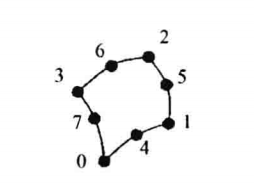
image

六角柱，三维基本类型，由6个四边形面、两个六边形面、18条边和12个顶点构成。点的连接顺序如图，六角柱的面和边不能与其他的相交且六角柱必须是凸的
2、非线性单元 
类型图示说明
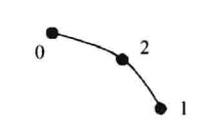
VTK_QUADRATIC_EDGE

image

二次曲线，一维基本类型，由三个点定义，其中前两个点分别对应曲线的端点，第三个点位于曲线的中间位置，曲线的方向是由第一个点指向第二个点
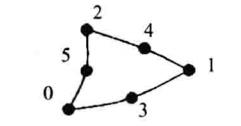
VTK_QUADRATIC_TRIANGLE

image

二次三角形，二维的基本类型之一，由六个点定义，其中前三个点对应三角形的三个顶点，另外三点分别对应三条边的中点

VTK_QUADRATIC_

LINEAR_QUAD

image

二次线性四边形，二维的基本类型之一，由六个点定义，其中前四个点对应四边形顶点，另外两个点位于第一和第三条边的中点处
VTK_QUADRATIC_QUAD

image

二次四边形，二维的基本类型之一，由八个点定义，其中前四个点对应四个顶点，后四点分别对应四条边的中点
VTK_BIQUADRATIC_QUAD

image

双二次四边形，二维的基本类型之一，由九个点定义，其中前四个点对应四个顶点，后四点分别对应四条边的中心，最后一个点位于该二次四边形的中心位置
VTK_QUADRATIC_TETRA

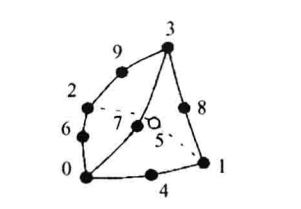
image

二次四面体，三维的基本类型之一，由10个点定义，其中前四个点对应四面体的四个顶点，其余六个点分别对应六条边的中点
VTK_QUADRATIC_PYRAMID

image

二次角锥体，三维的基本类型之一，由13个点定义，其中前五个点对应角锥体的五个顶点，其余八个点分别对应八条边的中点

VTK_QUADRATIC_

HEXAHEDRON

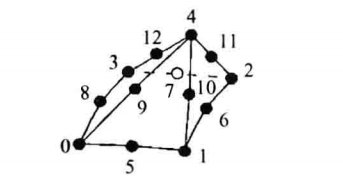
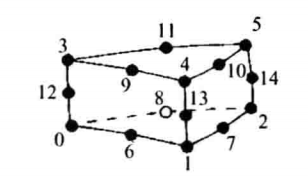
image

二次六面体，三维的基本类型之一，由20个点定义，其中前八个点对应六面体的八个顶点，其余12个点分别对应12条边的中点

VTK_BIQUADRATIC_

QUADRATIC_HEXAHEDRON

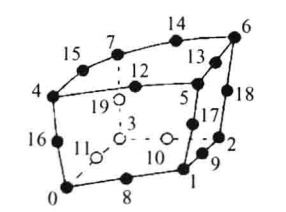
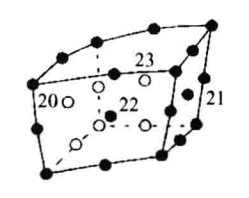
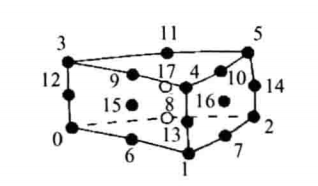
image

双二次六面体，三维的基本类型之一，由24个点定义，其中前八个点对应六面体的八个顶点，其余12个点分别对应12条边的中点，最后4个点位于前4面的中心位置

VTK_TRIQUADRATIC_

HEXAHEDRON

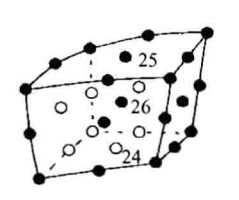
image

三次六面体，三维的基本类型之一，由27个点定义，其中前八个点对应六面体的八个顶点，其余12个点分别对应12条边的中点，另外6个点位于6个面的中心位置，最后一个点位于六面体的中心

VTK_QUADRATIC_

LINEAR_WEDGE

image

二次线性楔形体，三维的基本类型之一，由12个点定义，其中前六个点对应楔形体的六个顶点，其余六个点分别对应组成上下面两个面的三角形边的中点
VTK_QUADRATIC_WEDGE

image

二次楔形体，三维的基本类型之一，由15个点定义，其中前六个点对应楔形体的六个顶点，其余九个点分别对应九条边的中点

VTK_BIQUADRATIC_

QUADRATIC_WEDGE

image

双二次楔形体，三维的基本类型之一，由18个点定义，其中前六个点对应楔形体的六个顶点，九个点分别对应九条边的中点，最后三个点位于每个二次曲面的中心位置

四、数据属性

 属性数据(Attribute Data)是与数据集组织结构相关联的信息。

1、标量数据

        标量数据是数据集里的每个位置具有单值的数据，它只表示数据的大小，例如温度、压力、密度、高度等。标量数据是最简单也是最普遍的可视化数据。 

2、矢量数据

        与物理学的矢量概念一样，VTK的矢量数据也是指既有大小也有方向的量，三维方向上用三元组(Triple)表示为(u,v,w)，如速度、应力、位移等。 

3、纹理坐标

        为了使物体看起来更加真实，计算机图形学通常对显示的三维物体采用纹理映射。纹理坐标可以将点从笛卡儿坐标空间映射到一维、二维或三维的纹理空间中。 

4、张量数据

        张量是矢量和矩阵通过复杂的数学算法得到的，一个k阶的张量可当作一个k维的表格。零阶的张量是标量，一阶的张量是矢量，二阶的张量是纹理坐标，三阶的张量是一个三维阵列 。

五、不同类型的数据集 

1、vtklmageData

        vtkImageData 类型的数据是按规则排列在矩形方格中的点和单元的集合。

2、vtkPolyData

         多边形数据集 vtkPolyData由顶点(Vertex)、多顶点(Polyvertex)、线(Line)、折线(Polyline)和三角形条带(Triangle Strip)等单元构成，多边形数据是不规则结构的，并且多边形数据集的单元在拓扑维度上有多种类型。

3、vtkRectilinearGrid

         vtkRectilinearGrid 类型的数据是排列在矩形方格中的点和单元的集合。

4、vtkStructuredGrid

         vtkStructuredGrid 是结构化网格数据，具有规则的拓扑结构和不规则的几何结构，但是单元没有重叠或交叉。

5、vtkUnstructuredGrid

        vtkUnstructuredGrid 是非结构化网格，是最常见的数据集类型，它的拓扑结构和几何结构都是非结构化的，在此数据集中，所有单元类型都可以组成任意组合，所有单元的拓扑结构从零维延伸至三维。

 6、vtkUnstructuredPoints

         vtkUnstructuredPoints 为非结构化点集，是指不规则地分布在空间的点集。非结构化点集具有不规则的几何结构，不具有拓扑结构，非结构化点集用离散点来表达。

六、数据的存储与表达 

 1、vtkDataArray

         VTK 中的内存分配采用连续内存，可以快速地创建、删除和遍历，称之为数据数组(DataArray)，用类 vtkDataArray 实现。数组数据的访问是基于索引的，与C++一样，从零开始计数。

 

2、数据对象的表达

        VTK 里的数据对象是作为vtkDataArray的数组(即数据数组的数组)实现的。vtkDataObiect是一种通用的可视化数据的表达，可视化算法基本都没有直接处理vtkDataObiect 类型的数据，在处理某一类数据时，一般都要求数据内部具有某种组织结构。vtkDataObiect 内部封装了与可视化管线的执行相关的变量和方法，包括表达数据。在vtkDataObiect 内部有一个 vkFieldData(场数据)的实例，负责对数据的表达。场数据可以看作数据数组的数组，数组里的每一个元素都是一个数组，数组的类型、长度、元组的大小和名称等都可以各不相同。 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2072425.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

东南大学和东北大学

东南大学和东北大学

其实我五点多就醒了&#xff0c;生物钟天生如此&#xff0c;没办法。 只是在人家家里&#xff0c;不方便过早地有动静&#xff0c;而我的脑子&#xff0c;也还在酒力影响之下&#xff0c;并没有完全清楚&#xff0c;所以又闭目养神了一会儿。 看了几次时间&#xff0c;终于6点了…
阅读更多...
高仿115资源网dz论坛模板

高仿115资源网dz论坛模板

源码介绍 高仿115资源网dz论坛模板&#xff0c;首先去DZ论坛下个PHP版本安装好&#xff0c;把我们提供的模版上传到[template]目录。 本套模板是dz论坛仿115资源网开发的模板&#xff0c;dz论坛是腾讯旗下的论坛系统&#xff0c;非常的好用。 源码下载 高仿115资源网dz论坛模…
阅读更多...
C++ STL 关联容器

C++ STL 关联容器

系列文章目录 CSTL迭代器iterator设计 https://blog.csdn.net/surfaceyan/article/details/126772555 C STL 序列式容器(一 vector list) https://blog.csdn.net/surfaceyan/article/details/126860166 C STL 序列式容器(二 deque slist) https://blog.csdn.net/surfaceyan/ar…
阅读更多...
Vue中的methods方法与computed计算属性的区别

Vue中的methods方法与computed计算属性的区别

在创建的 Vue 应用程序实例中&#xff0c;可以通过 methods 选项定义方法。应用程序实例本身会代理 methods 选项中的所有方法&#xff0c;因此可以像访问 data 数据那样来调用方法。在模板中绑定表达式只能用于简单的运算。如果运算比较复杂&#xff0c;可以使用 Vue.js 提供的…
阅读更多...
求解向量中连续子向量的最大和

求解向量中连续子向量的最大和

开篇 本篇文章旨在求解向量中n个连续子向量的最大和。题目来源是《编程珠玑》第8章《算法设计技术》。 问题描述 输入:具有n个浮点数的向量x; 输出:输入向量的任何连续子向量中的最大和; 例如&#xff1a;输入向量为31,-41,59,26,-53,58,97,-93,-23,84; 那么输出就是从59到97五…
阅读更多...
基于java+springboot+mysql校园预约自习室网站43642-计算机毕业设计项目选题推荐（免费领源码）

基于java+springboot+mysql校园预约自习室网站43642-计算机毕业设计项目选题推荐（免费领源码）

摘要 在社会快速发展的影响下&#xff0c;教育事业蓬勃发展&#xff0c;大大增加了学校的数量、多样性、教育质量等要求&#xff0c;使教育的管理和运营比过去更加困难。依照这一现实为基础&#xff0c;设计一个快捷而又方便的校园预约自习室网站是一项十分重要并且有价值的事情…
阅读更多...
回归预测|基于北方苍鹰优化最小二乘支持向量机的数据预测Matlab程序NGO-LSSVM 多特征输入单输出 含基础程序

回归预测|基于北方苍鹰优化最小二乘支持向量机的数据预测Matlab程序NGO-LSSVM 多特征输入单输出 含基础程序

回归预测|基于北方苍鹰优化最小二乘支持向量机的数据预测Matlab程序NGO-LSSVM 多特征输入单输出 含基础程序 文章目录 前言回归预测|基于北方苍鹰优化最小二乘支持向量机的数据预测Matlab程序NGO-LSSVM 多特征输入单输出 含基础程序 一、NGO-LSSVM模型1. LSSVM&#xff08;最小…
阅读更多...
联网可视化：引领智能出行新时代

联网可视化：引领智能出行新时代

图扑车联网可视化系统整合数据监测与分析&#xff0c;提升交通管理效率&#xff0c;优化车辆调度&#xff0c;提高道路安全&#xff0c;为用户提供智能化、便捷的出行体验。
阅读更多...
使用Python实现方波信号傅里叶变换

使用Python实现方波信号傅里叶变换

目录 概述 1 方波信号 1.1 问题描述 1.2 傅里叶级数的数学实现 2 函数实现 2.1 方波信号实现 2.2 方波信号的傅里叶函数 3 测试函数 3.1 测试原理 3.2 改变K值的波形变化 概述 本文主要介绍使用使用Python实现方波信号傅里叶变换的方法&#xff0c;笔者首先介绍了方…
阅读更多...
如何使用ssm实现基于java的奶茶店管理系统的设计与实现

如何使用ssm实现基于java的奶茶店管理系统的设计与实现

TOC ssm140基于java的奶茶店管理系统的设计与实现jsp 第一章 绪 论 1.1背景及意义 系统管理也都将通过计算机进行整体智能化操作&#xff0c;对于奶茶店管理系统所牵扯的管理及数据保存都是非常多的&#xff0c;例如管理员&#xff1b;主页、个人中心、用户管理、奶茶分类管…
阅读更多...
Kubectl基础命令使用

Kubectl基础命令使用

一.Kubectl 基础命令 格式&#xff1a; kubectl [command] [TYPE] [NAME] [FLAGS] kubectl 是 Kubernetes 的命令行工具&#xff0c;用于管理 Kubernetes 集群。以下是一些常用的 kubectl 命令及其选项&#xff1a; 常用命令 获取资源 列出所有资源类型&#xff08;Pods、De…
阅读更多...
【C++】OJ习题 篇1

【C++】OJ习题 篇1

&#x1f680;个人主页&#xff1a;奋斗的小羊 &#x1f680;所属专栏&#xff1a;C 很荣幸您能阅读我的文章&#xff0c;诚请评论指点&#xff0c;欢迎欢迎 ~ 目录 &#x1f4a5;1、string&#x1f4a5;1.1 字符串相加&#x1f4a5;1.2 验证回文字符串&#x1f4a5;1.3 反转…
阅读更多...
【奇某信-注册/登录安全分析报告】

【奇某信-注册/登录安全分析报告】

前言 由于网站注册入口容易被黑客攻击&#xff0c;存在如下安全问题&#xff1a; 暴力破解密码&#xff0c;造成用户信息泄露短信盗刷的安全问题&#xff0c;影响业务及导致用户投诉带来经济损失&#xff0c;尤其是后付费客户&#xff0c;风险巨大&#xff0c;造成亏损无底洞…
阅读更多...
(论文解读)Domain Adaptation via Prompt Learning

(论文解读)Domain Adaptation via Prompt Learning

摘要 无监督域适应( UDA )旨在将从带有标签的源域数据中学习到的模型适应到未标注的目标域数据集。现有的UDA方法通过对齐源域和目标域特征空间来学习领域不变特征。这种对齐是通过约束实现的&#xff0c;例如统计差异最小化或对抗学习。 然而&#xff0c;这些约束会导致语义…
阅读更多...
【自动驾驶】控制算法（四）坐标变换与横向误差微分方程

【自动驾驶】控制算法（四）坐标变换与横向误差微分方程

写在前面&#xff1a; &#x1f31f; 欢迎光临 清流君 的博客小天地&#xff0c;这里是我分享技术与心得的温馨角落。&#x1f4dd; 个人主页&#xff1a;清流君_CSDN博客&#xff0c;期待与您一同探索 移动机器人 领域的无限可能。 &#x1f50d; 本文系 清流君 原创之作&…
阅读更多...
浙大版循环结构程序设计 7-6-1 贪心法-找零钱

浙大版循环结构程序设计 7-6-1 贪心法-找零钱

7-6-1 贪心法-找零钱 #include <stdio.h>int main(){int n5,n2,n1,money,total;int flag 1; //判断是否符合条件然后跳出循环scanf("%d",&money);if(money>100){printf("Invalid.");}for(n5money/5;(flag1)&&(n5>0);n5--){for(n2…
阅读更多...
2-75 基于matlab的多尺度小波核svm预测

2-75 基于matlab的多尺度小波核svm预测

基于matlab的多尺度小波核svm预测&#xff0c;数据归一化操作&#xff0c;尺度小波核函数作为核函数进行训练&#xff0c;训练后的模型进行预测。程序已调通&#xff0c;可直接运行。 2-75 多尺度小波核 SVM预测 - 小红书 (xiaohongshu.com)
阅读更多...
Java 认识String类

Java 认识String类

1. 创建字符串 常见的构造 String 的方式 //方式一&#xff1a;String str "hello world";//方式二&#xff1a;String str2 new String("Hello world");//方式三&#xff1a;char[] array {a,b,c};String str3 new String(array);注意事项&#xff1…
阅读更多...
Promise学习之初步认识Promise

Promise学习之初步认识Promise

目录 前言 一、认识Promise (一) 含义 (二) 代码演示 二、Promise状态 三、总结 前言 在上一篇的学习中&#xff0c;我们已经认识到了同步与异步&#xff0c;异步代码在解决同步代码问题的同时&#xff0c;也会产生一些新的问题&#xff0c;比如常说的回调地狱&#xff0…
阅读更多...
DBSCAN算法及Python实践

DBSCAN算法及Python实践

DBSCAN&#xff08;Density-Based Spatial Clustering of Applications with Noise&#xff0c;具有噪声的基于密度的空间聚类应用&#xff09;算法是一种基于密度的聚类算法&#xff0c;它在机器学习和数据挖掘领域有广泛的应用。以下是DBSCAN算法的主要原理和特点&#xff1a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023