1.1.1 线性dp
2.1.1 区间dp
3.1.1 背包dp
动态规划理论
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中, 可能会有很多可行解。没一个解都对应于一个值,我们希望找到具有最优值的解。胎动规划算法与分治法类似,其基本思想也是将待求解问题分解为若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适用于动态规划算法求解的问题,经分解得到的子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算很多次。如果我们能保存已解决子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划算法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
与分治法最大的差别是:适用于动态规划求解的问题,经分解后得到的子问题往往不是互相独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)
应用场景:
适用于动态规划的问题必须满足最优化原理、无后效性和重叠性。
(1) 最优化原理(最优子结构性质):一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
(2) 无后效性:将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称无后效性。
(3) 子问题的重叠性:动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这就是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他算法。
1.1.1线性DP
理论
线性动态规划,是较常见的一类动态规划问题,其是在线性结构上进行状态转移
不像背包问题、区间DP等有固定的模板(但是模版也相对固定,更多的是要通过题目来思考)
线性动态规划的目标函数为特定变量的线性函数,约束是这些变量的线性不等式或等式
目的是求目标函数的最大值或最小值
(直观理解来看,只要状态转移方程能写成分段函数的,在某种意义上都能说他是线性DP,但本质仍是需要去探究信息流动的过程)
因此,除了少量问题(如:LIS、LCS、LCIS等)有固定的模板外,大部分都要根据实际问题来推导得出答案
顾名思义,线性DP就是在一条线上进行DP,这里举一些典型的例子。
LIS问题(最长上升子序列问题)
题目
给定一个长度为N的序列A,求最长的数值单调递增的子序列的长度。
上升子序列B可表示为B={Ak1,Ak2,···,Akp},其中k1<k2<···<kp。
解析
状态:F[i]表示以A[i]为结尾的最长上升子序列的长度,边界为f[0]=0。
状态转移方程:F[i]=max{F[j]+1}(0≤j<i,A[j]<A[i])。
答案显然为max{F[i]}(1≤i≤N)。
事实上,无论是上升、下降还是不上升等等此类问题,代码都是相似的,唯一的区别只是判断的符号更改罢了。
Code
#include <iostream>
using namespace std;
int n,a[100],f[100],maxn;
int main()
{
f[0]=0;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
for(int j=1;j<n;j++)
if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
maxn=max(maxn,f[i]);
}
cout<<maxn;
return 0;
}LCS问题(最长公共子序列)
题目
给定两个长度分别为N、M的字符串A和B,求最长的既是A的子序列又是B的子序列的字符串的长度。
解析
状态:F[i][j]表示A的前i个字符与B的前j个字符中的最长公共子序列,边界为F[i][0]=F[0][j]=0。
状态转移方程:F[i][j]=max{F[i-1][j],F[i][j-1],F[i-1][j-1]+1(if A[i]=B[j])}。
答案为F[N][M]。
Code
#include <iostream>
using namespace std;
int n,a[100][100],f[100][100],maxn;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++) cin>>a[i][j];
f[1][1]=a[1][1];
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
{
f[i][j]=a[i][j]+f[i-1][j];
if(j>1) f[i][j]=max(f[i][j],a[i][j]+f[i-1][j-1]);
}
for(int i=1;i<=n;i++) maxn=max(maxn,f[n][i]);
cout<<maxn;
return 0;
}数字三角形
题目
给定一个N行的三角矩阵A,其中第i行有i列,从左上角出发,每次可以向下方或向右下方走一步,最终到达底部。
求把经过的所有位置上的数加起来,和最大是多少。
解析
状态:F[i][j]表示走到第i行第j列,和最大是多少,边界为F[1][1]=A[1][1]。
状态转移方程:F[i][j]=A[i][j]+max{F[i-1][j],F[i-1][j-1](if j>1)}。
答案为max{F[N][j]}(1≤j≤N)。
Code
#include <iostream>
using namespace std;
int n,a[100][100],f[100][100],maxn;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++) cin>>a[i][j];
f[1][1]=a[1][1];
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
{
f[i][j]=a[i][j]+f[i-1][j];
if(j>1) f[i][j]=max(f[i][j],a[i][j]+f[i-1][j-1]);
}
for(int i=1;i<=n;i++) maxn=max(maxn,f[n][i]);
cout<<maxn;
return 0;
}例题一:合唱队
题目
【题目描述】
N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2,…,K,他们的身高分别为T1,T2,…,TK, 则他们的身高满足T1<...<Ti>Ti+1>…>TK(1≤i≤K)。
你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
【输入格式】
共二行。
第一行是一个整数N(2≤N≤100),表示同学的总数。
第二行有n个整数,用空格分隔,第i个整数Ti(130≤Ti≤230)是第i位同学的身高(厘米)。
【输出格式】
一个整数,最少需要几位同学出列。
【输入样例】
8 186 186 150 200 160 130 197 220
【输出样例】
4
【数据规模】
对于50%的数据,保证有n≤20;
对于全部的数据,保证有n≤100。
解析
最少出列,就是最多留下。
分析一下队形,其实质便是先上升再下降,不难联想到最长上升子序列与最长下降子序列。
定义状态F[i][0/1],F[i][0]表示以第i个人为结尾的最长上升子序列,F[i][1]表示以第i个人为结尾的最长合唱队形,F数组初值都为1,。
所以前i个人的最长合唱队形为max(F[i][0],F[i][1])。
状态转移方程:
F[i][0]=max(F[i][0],F[j][0]+1(if T[i]>T[j]));(T[i]如题所述,j<i)
F[i][1]=max(F[i][1],a[j][0],a[j][1]+1(if T[i]<T[j]);
最后的答案为n-max(F[i][0],F[i][1])。
Code
#include <bits/stdc++.h>
using namespace std;
int n,t[101],f[101][2],ans;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>t[i];
for(int i=1;i<=n;i++)
{
f[i][0]=1;
for(int j=1;j<i;j++)
if(t[i]>t[j]) f[i][0]=max(f[i][0],f[j][0]+1);
}
for(int i=1;i<=n;i++)
{
f[i][1]=1;//初始值
for(int j=1;j<i;j++)
if(t[i]<t[j]) f[i][1]=max(f[i][1],max(f[j][0],f[j][1])+1);//动态转移方程
}
for(int i=1;i<=n;i++) ans=max(ans,max(f[i][0],f[i][1]));//寻找答案
cout<<n-ans;
return 0;
}![]()
View Code
例题二:导弹拦截
题目
【题目描述】
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
【输入格式】
1行,若干个整数。
【输出格式】
2行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
【输入样例】
389 207 155 300 299 170 158 65
【输出样例】
6 2
【数据规模】
导弹高度是≤50000的正整数,导弹个数≤100000。
注:O(n2) 100分,O(nlogn) 200分。
解析
非常经典的一道线性DP题目。
先来说说O(n2)的做法:
第一问显然是在求最长不上升子序列,定义状态F[i]表示以第i个数为结尾的最长不下降子序列。
状态转移方程:F[i]=max(F[i],F[j]+1(if a[i]<=a[j]))(a[i]表示第i个导弹的高度,j<i)。
第二问实际上是在求最长上升子序列,证明比较麻烦,这里便不给出了,自行理解一下。
与第一问求法相同,只需要把<=改成>即可。
这种做法只有100分,考虑一下优化。
以第一问为例,观察样例,不难发现,当F的值相同时,越后面的导弹高度越高。
所以我们可以用一个d[i]维护F值为i的序列的最后一个导弹的值,t记录当前求出的最长不上升子序列的长度,
然后在递推时判断a[d[i]](1≤i≤t)的值,若大于等于当前导弹高度,就更新F。
第二问同理。
优化之后,虽然依旧是O(n2)的做法,但其时间复杂度却很小,足以拿到200分。
O(nlogn)的做法有很多,例如二分、线段树什么的,这里便不再给出(懒),有兴趣的可以自己尝试做做。
Code
优化前O(N^2)(100分做法)
#include<bits/stdc++.h>
using namespace std;
int a[100001],f[100001],n,maxn=-1;
int main()
{
while(scanf("%d",&a[++n])==1) ;
n--;
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
if(a[i]<=a[j]) f[i]=max(f[i],f[j]+1);
maxn=max(maxn,f[i]);
}
printf("%d\n",maxn);
maxn=-1;
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
if(a[i]>a[j]) f[i]=max(f[i],f[j]+1);
maxn=max(maxn,f[i]);
}
printf("%d",maxn);
return 0;
}优化后二分做法O(N^2)200分做法:
#include<bits/stdc++.h>
using namespace std;
long long f[1000010],a[1000010],tot=0,s=1,d[1000010],t=0;
int main()
{
memset(d,0,sizeof(d));
while(scanf("%lld",&a[++tot])==1);
tot--;
for(int i=1;i<=tot;i++)
{
f[i]=1;
for(int j=t;j>=1;j--)
if(a[i]<=a[d[j]])
f[i]=max(f[i],f[d[j]]+1);
t=max(f[i],t);
d[f[i]]=i;
}
cout<<t<<endl;
t=0;
for(int i=1;i<=tot;i++)
{
f[i]=1;
for(int j=t;j>=1;j--)
if(a[i]>a[d[j]])
f[i]=max(f[i],f[d[j]]+1);
t=max(f[i],t);
d[f[i]]=i;
}
cout<<t;
return 0;
}2.1.1区间DP
一、问题
给定长为n的序列a[i],每次可以将连续一段回文序列消去,消去后左右两边会接到一起,求最少消几次能消完整个序列,n≤500。
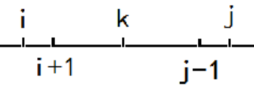
f[i][j]表示消去区间[i,j]需要的最少次数。
则
![]()
;
若a[i]=a[j],则还有
![]()
。
这里实际上是以区间长度为阶段的,这种DP我们通常称为区间DP。
区间DP的做法较为固定,即枚举区间长度,再枚举左端点,之后枚举区间的断点进行转移。
二、概念
区间类型动态规划是线性动态规划的拓展,它在分阶段划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。(例:f[i][j]=f[i][k]+f[k+1][j])
区间类动态规划的特点:
- 合并:即将两个或多个部分进行整合。
- 特征:能将问题分解成为两两合并的形式。
- 求解:对整个问题设最优值,枚举合并点,将问题分解成为左右两个部分,最后将左右两个部分的最优值进行合并得到原问题的最优值。
三、例题
【例题一】石子合并:
【问题描述】
将n(1≤n≤200)堆石子绕圆形操场摆放,现要将石子有次序地合并成一堆。规定每次只能选相邻的两堆石子合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 (1)选择一种合并石子的方案,使得做n-1次合并,得分的总和最小。 (2)选择一种合并石子的方案,使得做n-1次合并,得分的总和最大。
【样例输入】
4
4 5 9 4
【样例输出】
43
54
贪心解法:
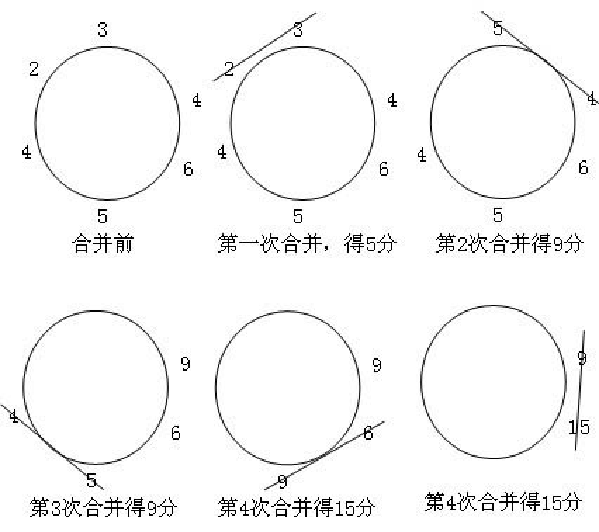
贪心共62分☝
正解共61分☟
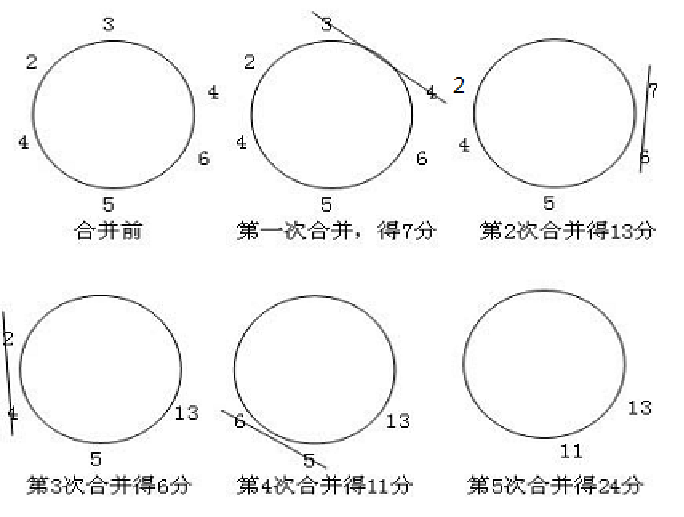
【思路点拨】
无环正解: 对应到动态规划中,就是两个长度较小的区间上的信息向一个更长的区间发生了转移,划分点k就是转移的决策,区间长度len就是DP的阶段。根据动态规划“选择最小的能覆盖状态空间的维度集合”的思想,可以只用左、右端点表示DP的状态。
sum[i]:从第1堆到第i堆石子数总和。
Fmax[i][j]:将从第i堆石子合并到第j堆石子的最大得分;
Fmin[i][j]:将从第i堆石子合并到第j堆石子的最小得分;
初始条件:Fmax[i][i]=0,Fmin[i][i]=INF
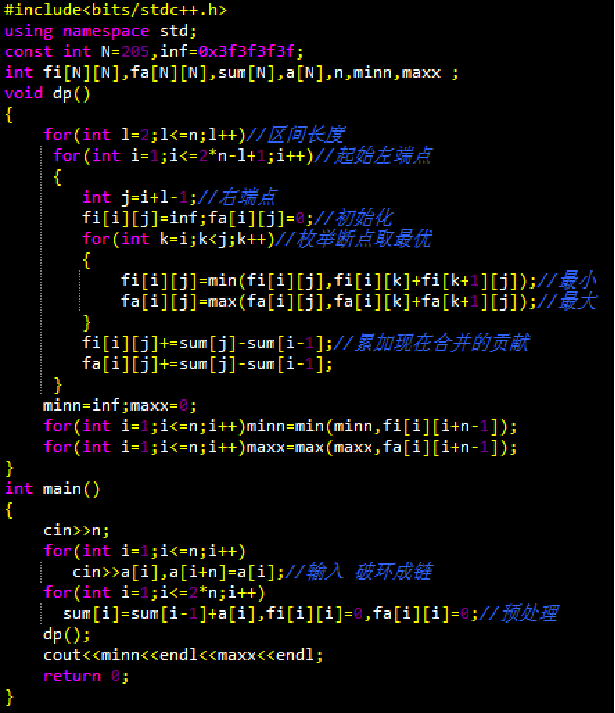
则状态转移方程为:(其中i<=k<j)
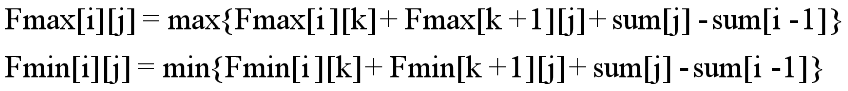
时间复杂度为

。
【环的处理】破环成链
注意到:题目中石子是围成一个圈,而不是一条线。
- 方法1:由于石子堆是围成一个圈,因此我们可以枚举分开的位置,首先将这个圈转化为链,因此要做n次,这样时间复杂度为 。
- 方法2:将这条链延长2倍,扩展成2n-1堆,其中第1堆与n+1堆完全相同,第i堆与n+i堆完全相同,这样只要对这2n堆动态规划后,枚举f(1,n),f(2,n+1),…,f(n,2n-1)取最优值即可。时间复杂度为 ,如下图:

【例题二】凸多边形的划分:
【问题描述】
给定一个具有N(N≤50)个顶点(从1到N编号)的凸多边形,每个顶点的权均是一个正整数。问:如何把这个凸多边形划分成N-2个互不相交的三角形,使得这些三角形顶点的权的乘积之和最小?
【输入示例】
5
121 122 123 245 231
【输出示例】
12214884
【题目分析】
如果我们按顺时针将顶点编号,从顶点i到顶点j的凸多边形表示为如下图:
设f[i][j](i<j)表示从顶点i到顶点j的 凸多边形三角剖分后所得到的最大乘积,当 前我们可以枚举点k,考虑凸多边形(i,j)中 剖出三角形(i,j,k),凸多边形(i,k), 凸多边形(k,j)的最大乘积和。我们可以得到 动态转移方程:(1<=i<k<j<=n)
![]()
初始条件:f[i][i+1]=0; 目标状态:f[1][n];
时间复杂度为:
![]()
。
但我们可以发现,由于这里为乘积之和,在输入数据较大时有可能超过长整形范围,所以还需用高精度计算
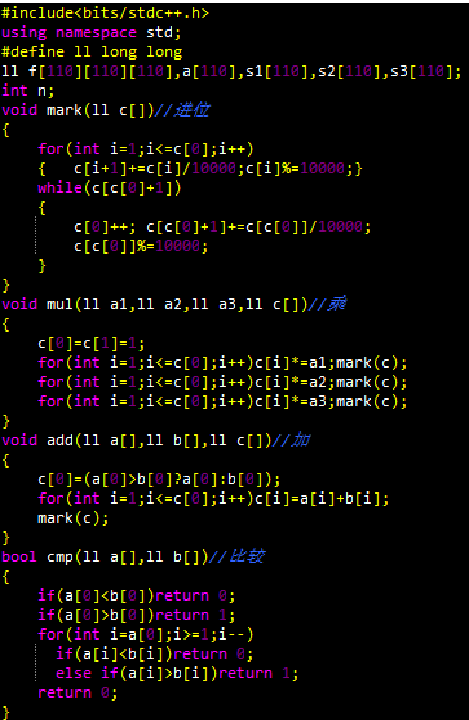
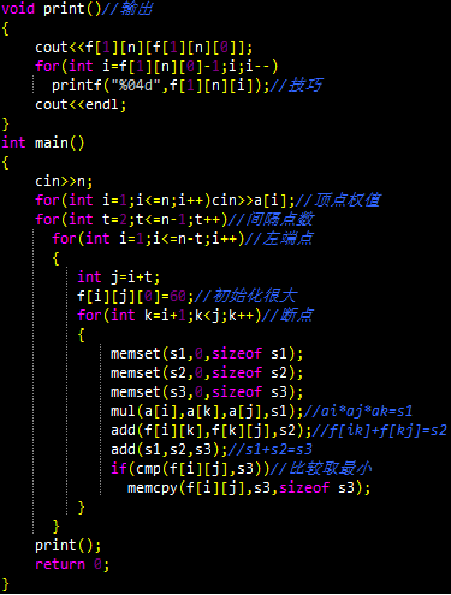
【总结】
基本特征:将问题分解成为两两合并的形式。
解决方法:对整个问题设最优值,枚举合并点,将问题分解成为左右两个部分,再将左右两个部分的最优值进行合并得到原问题的最优值。
设i到j的最优值,枚举剖分(合并)点,将(i,j)分成左右两区间,分别求左右两边最优值,如下图:

状态转移方程的一般形式如下:
![]()
3.1.1背包DP
01背包
给定 n 种物品和一个容量为 C 的背包,物品 i 的重量是 wi,其价值为 vi 。
问:应该如何选择装入背包的物品,使得装入背包中的物品的总价值最大?
分析一波,面对每个物品,我们只有选择拿取或者不拿两种选择,不能选择装入某物品的一部分,也不能装入同一物品多次。
解决办法:声明一个 大小为 m[n][c] 的二维数组,m[ i ][ j ] 表示 在面对第 i 件物品,且背包容量为 j 时所能获得的最大价值 ,那么我们可以很容易分析得出 m[i][j] 的计算方法,
(1). j < w[i] 的情况,这时候背包容量不足以放下第 i 件物品,只能选择不拿
m[ i ][ j ] = m[ i-1 ][ j ]
(2). j>=w[i] 的情况,这时背包容量可以放下第 i 件物品,我们就要考虑拿这件物品是否能获取更大的价值。
如果拿取,m[ i ][ j ]=m[ i-1 ][ j-w[ i ] ] + v[ i ]。 这里的m[ i-1 ][ j-w[ i ] ]指的就是考虑了i-1件物品,背包容量为j-w[i]时的最大价值,也是相当于为第i件物品腾出了w[i]的空间。
如果不拿,m[ i ][ j ] = m[ i-1 ][ j ] , 同(1)
究竟是拿还是不拿,自然是比较这两种情况那种价值最大。
由此可以得到状态转移方程:
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];例:0-1背包问题。在使用动态规划算法求解0-1背包问题时,使用二维数组m[i][j]存储背包剩余容量为j,可选物品为i、i+1、……、n时0-1背包问题的最优值。绘制
价值数组v = {8, 10, 6, 3, 7, 2},
重量数组w = {4, 6, 2, 2, 5, 1},
背包容量C = 12时对应的m[i][j]数组。

(第一行和第一列为序号,其数值为0)
如m[2][6],在面对第二件物品,背包容量为6时我们可以选择不拿,那么获得价值仅为第一件物品的价值8,如果拿,就要把第一件物品拿出来,放第二件物品,价值10,那我们当然是选择拿。m[2][6]=m[1][0]+10=0+10=10;依次类推,得到m[6][12]就是考虑所有物品,背包容量为C时的最大价值。
#include <iostream>
#include <cstring>
using namespace std;
const int N=15;
int main()
{
int v[N]={0,8,10,6,3,7,2};
int w[N]={0,4,6,2,2,5,1};
int m[N][N];
int n=6,c=12;
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
return 0;
}到这一步,可以确定的是可能获得的最大价值,但是我们并不清楚具体选择哪几样物品能获得最大价值。
另起一个 x[ ] 数组,x[i]=0表示不拿,x[i]=1表示拿。
m[n][c]为最优值,如果m[n][c]=m[n-1][c] ,说明有没有第n件物品都一样,则x[n]=0 ; 否则 x[n]=1。当x[n]=0时,由x[n-1][c]继续构造最优解;当x[n]=1时,则由x[n-1][c-w[i]]继续构造最优解。以此类推,可构造出所有的最优解。(这段全抄算法书,实在不知道咋解释啊。。)
void traceback()
{
for(int i=n;i>1;i--)
{
if(m[i][c]==m[i-1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
}
x[1]=(m[1][c]>0)?1:0;
}例:
某工厂预计明年有A、B、C、D四个新建项目,每个项目的投资额Wk及其投资后的收益Vk如下表所示,投资总额为30万元,如何选择项目才能使总收益最大?

结合前面两段代码
#include <iostream>
#include <cstring>
using namespace std;
const int N=150;
int v[N]={0,12,8,9,5};
int w[N]={0,15,10,12,8};
int x[N];
int m[N][N];
int c=30;
int n=4;
void traceback()
{
for(int i=n;i>1;i--)
{
if(m[i][c]==m[i-1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
}
x[1]=(m[1][c]>0)?1:0;
}
int main()
{
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];
}
}/*
for(int i=1;i<=6;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
*/
traceback();
for(int i=1;i<=n;i++)
cout<<x[i];
return 0;
}完全背包
问题
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
基本思路
这个问题非常类似于01背包问题,所 不同的是每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很多种。如果仍然按照解 01背包时的思路,令f[i][j]表示前i种物品恰放入一个容量为c的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样:
f[i][j]=max{f[i-1][j-k*w[i]]+k*v[i]|0<=k*c[i]<=v}
这跟01背包问题一样有O(VN)个状态需要求解,但求解每个状态的时间已经不是常数了,求解状态f[i][v]的时间是O(v/c[i]),总的复杂度可以认为是O(V*Σ(V/c[i])),是比较大的。
将01背包问题的基本思路加以改进,得到了这样一个清晰的方法。这说明01背包问题的方程的确是很重要,可以推及其它类型的背包问题。但我们还是试图改进这个复杂度。
其中F[i-1][j-k*w[i]]+k*v[i]表示前i-1种物品中选取若干件物品放入剩余空间为j-k*w[i]的背包中所能得到的最大价值加上k件第i种物品的总价值;
设物品种数为n,背包容量为c,第i种物品体积为w[i],第i种物品价值为v[i]。
代码1:
#include<bits/stdc++.h>
using namespace std;
int dp[1001][1001];
int w[1001];
int v[1001];
int main()
{
int n,c;
while(scanf("%d%d",&n,&c)!=EOF)
{
int i,j;
memset(dp,0,sizeof(dp));
for(i=1; i<=n; i++)
scanf("%d",&w[i]);
for(i=1; i<=n; i++)
scanf("%d",&v[i]);
for(i=1; i<=n; i++)
{
for(j=0; j<=c; j++)
{
for(int k=0; k*w[i]<=j; k++)
dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);//表示前i-1种物品中选取若干件物品放入剩余空间为j-k*w[i]的背包中所能得到的最大价值加上k件第i种物品的总价值;
}
}
printf("%d\n",dp[n][c]);
}
return 0;
}简单优化:筛选
这个筛选过程如下:先找出体积大于背包的物品直接筛掉一部分(也可能一种都筛不掉),然后筛选出同体积但价值大的物品,其余的都筛掉(这也可能一件都筛不掉)即若两件物品满足w[i] ≤w[j]&&v[i] ≥v[j]时将第j种物品直接筛选掉。因为第i种物品比第j种物品物美价廉,用i替换j得到至少不会更差的方案。
转化为01背包:
因为同种物品可以多次选取,那么第i种物品最多可以选取c/w[i]件价值不变的物品,然后就转化为01背包问题。整个过程的时间复杂度并未减少。
如果把第i种物品拆成体积为w[i]×2k价值v[i]×2k的物品,其中满足w[i]×2k≤V。那么在求状态F[i][j]时复杂度就变为O(log2(V/C[i]))。整个时间复杂度就
变为O(NVlog2(c/w[i]))
将原始算法的DP思想转变一下。
设F[i][j]表示出在前i种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现,我们对第i种物品放不放入背包
进行决策。如果不放那么F[i][j]=F[i-1][j];如果确定放,背包中应该出现至少一件第i种物品,所以F[i][j]种至少应该出现一件第i种物品,
即F[i][j]=F[i][j-w[i]]+v[i]。为什么会是F[i][j-w[i]]+v[i]?因为我们前面已经最大限度的放了第i件物品,如果能放就放这最后的一件,
(或者理解为前面已经往背包中放入了第i件物品,我们每一次只增加一件的往背包里放,而且只能增加一件,多了放不下)
代码2:
#include<bits/stdc++.h>
using namespace std;
int dp[1010][1010];
int w[1010];
int v[1010];
int main()
{
int n,c;
while(scanf("%d%d",&n,&c)!=EOF)
{
memset(dp,0,sizeof(dp));
int i,j;
for(i=1; i<=n; i++)
scanf("%d",&w[i]);
for(i=1; i<=n; i++)
scanf("%d",&v[i]);
for(i=1; i<=n; i++)
{
for(j=0; j<=c; j++)
{
if(j>=w[i])
dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);//注意此处与0-1背包的不同,0-1背包:max(dp[i-1][j],dp[i-1][j-w[i]+v[i])
else
dp[i][j]=dp[i-1][j];
}
}
printf("%d\n",dp[n][c]);
}
return 0;
}
一维解法:
和01背包问题一样,完全背包也可以用一维数组来保存数据。算法样式和01背包的很相似,唯一不同的是对V遍历时变为正序,而01背包为逆序
。01背包中逆序是因为F[i][]只和F[i-1][]有关,且第i件的物品加入不会对F[i-1][]状态造成影响。而完全背包则考虑的是第i种物品的出现的问题,
第i种物品一旦出现它势必应该对第i种物品还没出现的各状态造成影响。也就是说,原来没有第i种物品的情况下可能有一个最优解,现在第i种物品
出现了,而它的加入有可能得到更优解,所以之前的状态需要进行改变,故需要正序。
代码:
#include<bits/stdc++.h>
using namespace std;
int dp[1010];
int w[1010];
int v[1010];
int main()
{
int n,c;
while(scanf("%d%d",&n,&c)!=EOF)
{
int i,j,k;
memset(dp,0,sizeof(dp));
for(i=1;i<=n;i++)
scanf("%d",&w[i]);
for(i=1;i<=n;i++)
scanf("%d",&v[i]);
for(i=1;i<=n;i++)
{
for(j=w[i];j<=c;j++)//注意此处与0-1背包的不同,0-1为倒序(j=c;j>=w[i];j--)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
printf("%d\n",dp[c]);
}
return 0;
}
}分组背包
分组背包,即一开始选取的物品以及分成几个组,在选取时,可以从一个分组中选取一件物品或者一件物品也不选取,以此到达最大价值的选取目的。其方程也可以写成类似于“01背包”的方程,如下:
c[k][j] = max(c[k-1][j], c[k-1][j-w[k-1][i]]+v[k-1][i])
其中,k表示当前分组号,i表示当前分组中的第i件物品。以下为具体题目示例。
假设:有一个容量为10 Kg的背包,现有3个分组,其中每个分组的信息如下表,求如何选取可获最大价值。

具体题目:
可能会出现的情况:

上述表格从上至下、从左到右生成。以下为实现该算法的Java代码:
//一维数组,要注意组别和组中元素循环的位置
private static int[] BP_method06_1D(int m,int n,int[][] w,int[][] v){
int c[] = new int[m+1];
for (int i = 0; i < n; i++) {
c[i] = 0;//不必完全装满,则全部初始化为0
}
List<Integer> list = new ArrayList<>();
for (int k = 0; k < n; k++) {//组别
for (int j = m; j >= 1; j--) {//限定总重量
for (int i = 0; i < w[i].length; i++) {
if (j >= w[k][i]) {
c[j] = Math.max(c[j-w[k][i]] + v[k][i], c[j]);
}else {
c[j] = c[j];
}
}
}
}
return c;
}
//二维数组实现该算法,从理解上更为容易,但是要注意在可能出现的情况中要选择的是最大值还是最小值
private static int[][] BP_method06_2D(int m,int n,int[][] w,int[][] v){
int c[][] = new int[n+1][m+1];
for (int i = 0; i < n+1; i++) {
c[i][0] = 0;
}
for (int i = 0; i < m+1; i++) {
c[0][i] = 0;
}
List<Integer> list = new ArrayList<>();
for (int k = 1; k <= n; k++) {//组别
for (int j = 0; j <= m; j++) {//限定总重量
list.clear();
for (int i = 0; i < w[k-1].length; i++) {
if (j >= w[k-1][i]) {
list.add(Math.max(c[k-1][j], c[k-1][j-w[k-1][i]]+v[k-1][i]));
}else {
list.add(c[k-1][j]);
}
c[k][j] = Collections.max(list);
}
}
}
return c;
}
其输出结果如下: