行列式是什么-运算规则
-
排列:不同的 n 元排列共有 n! 个
-
逆序:小数排在大数后面,叫逆序;一个排列中逆序的总和叫做这个排列的逆序数,记为 τ ( j 1 , . . . , j n ) \tau(j_1,...,j_n) τ(j1,...,jn)
-
逆序数的计算方法:

-
奇排列和偶排列:逆序数为偶数的排列为偶排列,逆序数为奇数的排列为奇排列
【举例】求排列 n(n-1) … 321 的逆序数
最终计算借助等差数列求和公式: S n = ( n ( a 1 + a n ) ) / 2 S_n=(n(a_1+a_n))/2 Sn=(n(a1+an))/2
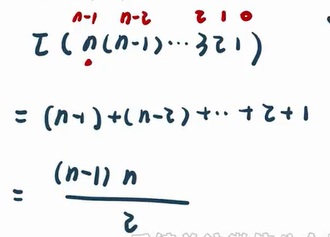
【注🧨】 记住公式:
(
(
n
−
1
)
n
)
/
2
((n-1)n)/2
((n−1)n)/2
行列式的定义
- 行列式是一个 n 行 n 列的方阵
- 行列式的计算结果是一个数,称为行列式值
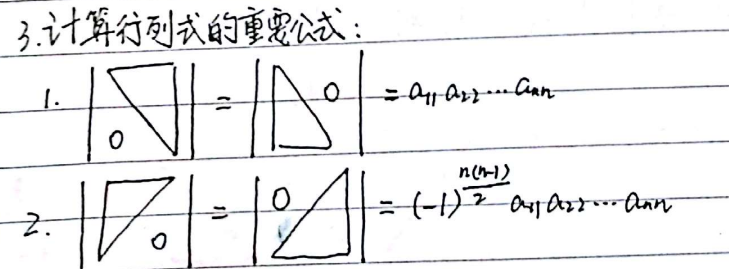
- 二阶和三阶行列式的计算遵循对角线法则,且对角线法则只适用于二阶行列式和三阶行列式
- 三阶行列式的计算公式:①主对角线同方向的元素相加,减去副对角线同方向的元素,几阶同方向划线的元素就有几个
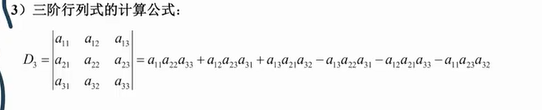
②加项的逆序数是偶数,减项的逆序数是奇数,列标是 j 1 , j 2 , j 3 j_1,j_2,j_3 j1,j2,j3 的某种排列组合(是看列标的逆序数),行标顺排 - n 阶行列式的计算:行标顺排,加项的逆序数是偶数,减项的逆序数是奇数,列标是 j 1 , j 2 , j 3 j_1,j_2,j_3 j1,j2,j3 的某种排列组合,取过的列不要取了,一共有 n! 项
【例题】
5 阶行列式 D 5 D_5 D5 展开式中有一项 a 15 a 52 a 44 a 31 a 23 a_{15}a_{52}a_{44}a_{31}a_{23} a15a52a44a31a23,此项的符号为:负号,逆序数为 7
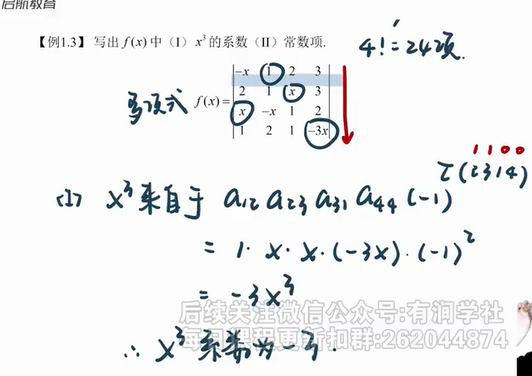
【题型🔴】问几次方的系数和常数项
系数:从行开始,从 a 11 a_{11} a11 开始, a 11 a_{11} a11 所在行列元素不看,看剩下元素与 a 11 a_{11} a11 相乘是否能得到题设的次方项,能得到写出元素顺序,并乘以(-1)的列表的逆序数次方
常数项:常数项其实是当所有的未知数地方都得 0,计算行列式的结果
真题:2021 数三 15 题

行列式的性质
- 行列式的行与列(按原顺序)互换(转置),行列式的值不变
- 行列式的两行(列)互换,行列式的值反号(添负号)–(对换)
- 【推论:】如果行列式中有两行(列)完全相同,则行列式的值为零
- 行列式的某行(列)每个元素都乘常数 k,则等于用 k 乘此行列式的值–(提公因子)
- 【推论:】
- 若行列式中某行(列)元素全为零,则行列式的值为零
- 若行列式中某行(列)有公因子 k,则可将 k 提到行列式外
- 若行列式中两行(列)对应元素成比例,其值为零
- 如果行列式某行(列)元素都写成两数之和,则该行列式可以写成两个行列式之和–(行列式的拆分)
⭐5. 将行列式的某行(列)的每个元素都乘常数 k,再加到另一行(列)的对应元素上,行列式的值不变 --(恒等变形【倍加】)符号表示:
r
j
+
k
r
i
r_j+kr_i
rj+kri,被操作行/列写在前面,只动第 j 行(固定写法)
【应用】适用于任何 n 阶行列式化三角形
⭐拉普拉斯公式(分块三角行列式)

- C 不一定是方阵也可以使用拉普拉斯公式
行列式按行/列展开定理
- 余子式和代数余子式
【注】
- 余子式和代数余子式都是行列式,结果都是一个数值
- 余子式和代数余子式值与 a i j a_{ij} aij 的具体取值无关,只与 a i j a_{ij} aij 的位置有关
-
余子式 M i j M_{ij} Mij:在 n 阶行列式中,把元素 a i j a_{ij} aij 所在的第 i 行第 j 列划去后,由剩余的元素按原位置顺序所构成的 n-1 阶行列式,称为元素 a i j a_{ij} aij 的余子式,记作 M i j M_{ij} Mij
-
代数余子式 A i j A_{ij} Aij: ( − 1 ) i + j M i j (-1)^{i+j}M_{ij} (−1)i+jMij 称为元素 a i j a_{ij} aij 的代数余子式,记为 A i j A_{ij} Aij,即 A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
-
应用:行列式计算

- 行列式按行/列展开定理(目的:降阶)
【定理】:行列式的值等于其任一行/列的各元素与其对应代数余子式的乘积之和
【适用】:选 0 多的行/列展开,0 不够多,就先化零,然后再展开
按行还是按列,看哪个不动,另一个递增
行列式的计算
常见行列式计算
计算行列式的常见题型和方法
- 化零降解法 (坚守原则:“打洞”,“降阶”)
【方法】:先利用性质将行列式的某一行或某一列化到只有一个元素不为 0,再用行列式展开定理化为低一阶的行列式(化零降阶法是计算行列式的主要方法)
【题型🔴】一点两斜—方法:按“.”所在行/列展开

【例题】

⭐2. 化三角形行列式
⭐⭐【类型 1】各行/列元素之和相等的行列式(各行全部加到第一行/列)
【例题】
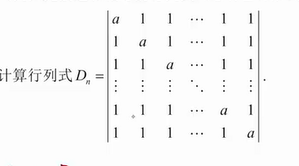
【固定解题流程】
①各行加至第一行
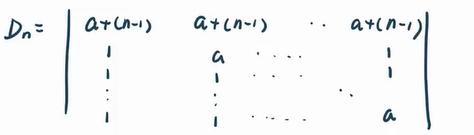
②提公因子
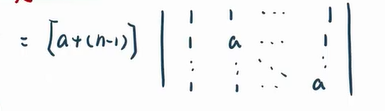
③各行减第一行
r
1
r_1
r1,化三角形

【类型 2】爪型行列式(各行倍加到第一行,“消去平爪”)
【例题】
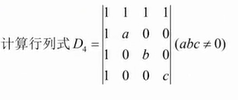
【固定解题流程】第二个非零,用第二行乘一个倍数加到第一行,第三个非零用第三行…,依此类推,第一个元素承受所有
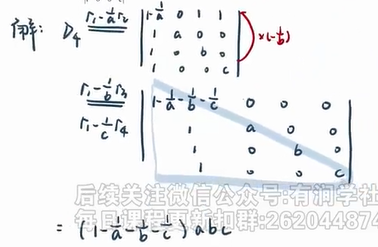
【类型 3】三对角行列式(逐行相减,化三角行列式)–主/副对角线有非零元,最近的平行线有非零元,其余部分均为 0
常见方法有:化三角形(低阶)、递推法(n 阶)、数学归纳法(n 阶)
【例题】
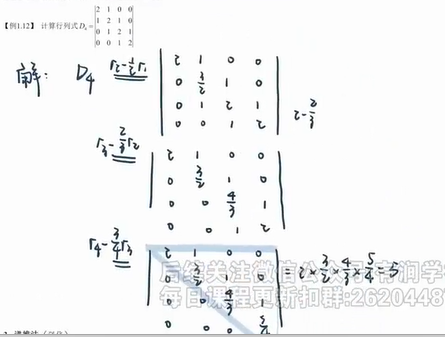
【方法】递推法
#todo待补充
【方法】数学归纳法
数学归纳法是证明(计算)行列式常用的方法,首先建立递推关系,当递推关系仅涉及相邻两阶行列式时 D n = 2 D n − 1 + 1 D_n=2D_{n-1}+1 Dn=2Dn−1+1,采用第一归纳法;当递推关系涉及相邻三阶行列式时 D n = 2 D n − 1 − D n − 2 D_n=2D_{n-1}-D_{n-2} Dn=2Dn−1−Dn−2,采用第二归纳法
第一数学归纳法
①设有一个与自然数 n 有关的命题,若当 n=1 时命题成立(
D
1
D_1
D1)
②假设当 n=k 时命题成立,可以推出当
n
=
k
+
1
n=k+1
n=k+1 时命题成立
那么命题对一切自然数 n 都成立
第二数学归纳法
设有一个与自然数 n 有关的命题,若
①当 n=1 和 n=2 时命题成立
②假设对
n
<
k
n<k
n<k 的一切自然数都成立,则 n=k 时命题也成立
那么命题对一切自然数 n 都成立
⭐【类型 4】范德蒙行列式
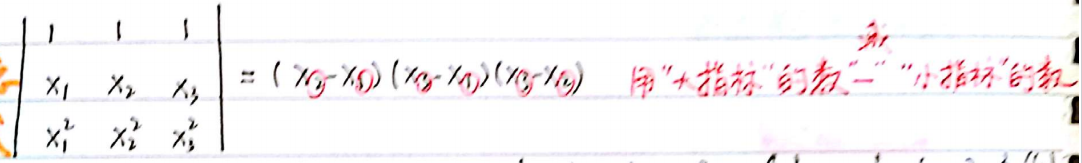
后减前
【识别】范德蒙行列式特点
1)第一行全为 1
2)第二行随便写
3)第三行往下的行依次升幂排列 (2,3 总结:构成一个以
x
i
x_i
xi 为公比的等比数列)
【应用】例题:

- 将最后一行换到第一行,其他行顺序不变,方法:逐行对换,注意负号(最后一行 n,然后 n-1, 然后 n-2 直到第一行)
- 此时新行列式的值 ( − 1 ) n − 1 D n (-1)^{n-1}D_n (−1)n−1Dn,与原行列式的值 D n D_n Dn,注意符号
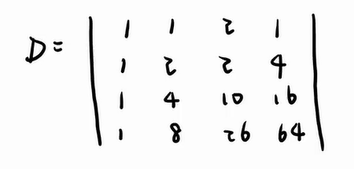
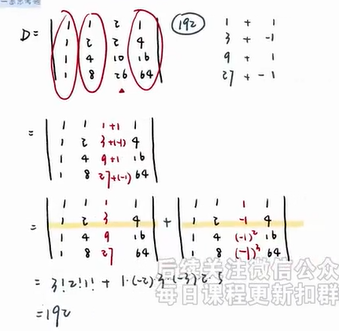
行列式按行/列展开定理的推论


⭐【原行列式将第 i 行元素替换为系数 x i x_i xi 之后,计算得到的新行列式】–直接作为套路
按照第几行展开,直接将第几行的数换成代数余子式的系数,进行计算,看第几行的时候直接看代数余子式的行标 A 即可
【例题】


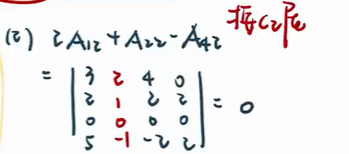
行列式的应用-克拉默法则
- 方程组解,在第四章学习