打饭
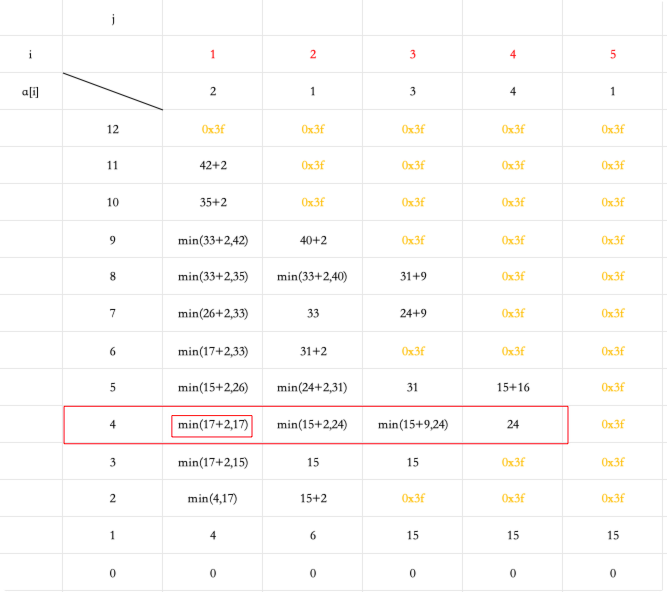
我还不信了,手动模拟一遍
再来了好看一点的图
| j | ||||||
|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | |
| a[i] | 2 | 1 | 3 | 4 | 1 | |
| 12 | 0x3f | 0x3f | 0x3f | 0x3f | 0x3f | |
| 11 | 42+2 | 0x3f | 0x3f | 0x3f | 0x3f | |
| 10 | 35+2 | 0x3f | 0x3f | 0x3f | 0x3f | |
| 9 | min(33+2,42) | 40+2 | 0x3f | 0x3f | 0x3f | |
| 8 | min(33+2,35) | min(33+2,40) | 31+9 | 0x3f | 0x3f | |
| 7 | min(26+2,33) | 33 | 24+9 | 0x3f | 0x3f | |
| 6 | min(17+2,33) | 31+2 | 0x3f | 0x3f | 0x3f | |
| 5 | min(15+2,26) | min(24+2,31) | 31 | 15+16 | 0x3f | |
| 4 | min(17+2,17) | min(15+2,24) | min(15+9,24) | 24 | 0x3f | |
| 3 | min(6+2,15) | 15 | 15 | 0x3f | 0x3f | |
| 2 | min(4,17) | 15+2 | 0x3f | 0x3f | 0x3f | |
| 1 | 4 | 6 | 15 | 15 | 15 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
前台样例整理结果如下
| j | ||||||
|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | |
| a[i] | 2 | 1 | 3 | 4 | 1 | |
| 12 | 0x3f | 0x3f | 0x3f | 0x3f | 0x3f | |
| 11 | 44 | 0x3f | 0x3f | 0x3f | 0x3f | |
| 10 | 37 | 0x3f | 0x3f | 0x3f | 0x3f | |
| 9 | 35 | 42 | 0x3f | 0x3f | 0x3f | |
| 8 | 35 | 35 | 40 | 0x3f | 0x3f | |
| 7 | 28 | 33 | 33 | 0x3f | 0x3f | |
| 6 | 19 | 33 | 0x3f | 0x3f | 0x3f | |
| 5 | 17 | 26 | 31 | 31 | 0x3f | |
| 4 | 17 | 17 | 24 | 24 | 0x3f | |
| 3 | 8 | 15 | 15 | 0x3f | 0x3f | |
| 2 | 4 | 17 | 0x3f | 0x3f | 0x3f | |
| 1 | 4 | 6 | 15 | 15 | 15 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
第二层循环中的 N / i N / i N/i的优化,因为a[i]克数的粮食要运回,应该尽可能少的让离得远又重的的窗口能打,应该让离得远但是量很少足够在到前面窗口的时候由于前面窗口a[i]很大即使离起点近也可能会产生大花费,而被选中
比如下图
所以,即使当离得远的很大时,其实可以直接不用考虑在第二层循环里的离得远的又重的,如果走到前面有可替代方案,自然会自动取最小。
数学证明还不会,感觉需要用到累加求和➕放缩
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define int long long
const int N=1e6+10;
int a[N],w[N];
int f[N];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,q;
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=n;i>=1;i--)
{
for(int j=N/i;j>a[i];j--)
{
f[j]=min(f[j],f[j-a[i]]+a[i]*i);
}
int val=(a[i]+2)*i;
f[a[i]]=min(f[a[i]],val);
}
//如果离得远的窗口能用更少的费用应该传递到靠得近的窗口那去
for(int i=N-2;i;i--) f[i]=min(f[i],f[i+1]);
for(int i=1;i<=q;i++)
{
int x;
cin>>x;
//upper_bound是找到等于x的那一位的下一位
int res=upper_bound(f,f+N,x)-f;
cout<<res-1<<endl;
}
//for(int i=0;i<=12;i++) cout<<f[i]<<' ';
//cout<<endl;
return 0;
}