论文地址:https://aclanthology.org/2022.acl-short.75.pdf
1. 摘要
多标签文本分类(MLTC)是自然语言处理中的一项基本且具有挑战性的任务。以往的研究主要集中在学习文本表示和建模标签相关性上。然而,在预测特定文本的标签时,通常忽略了现有的类似实例中的丰富知识。为了解决这一问题,作者提出了一个k最近邻(kNN)机制,该机制检索几个相邻实例并用它们的标签值作为模型的输出。此外,作者设计了一个多标签对比学习目标,使模型学习到kNN的分类过程,并提高了在推理过程中检索到的相邻实例的质量。实验表明,该方法可以为多个MLTC模型带来一致的和可观的性能改进,包括SOTA的预训练和非预训练模型。
2. 方案介绍
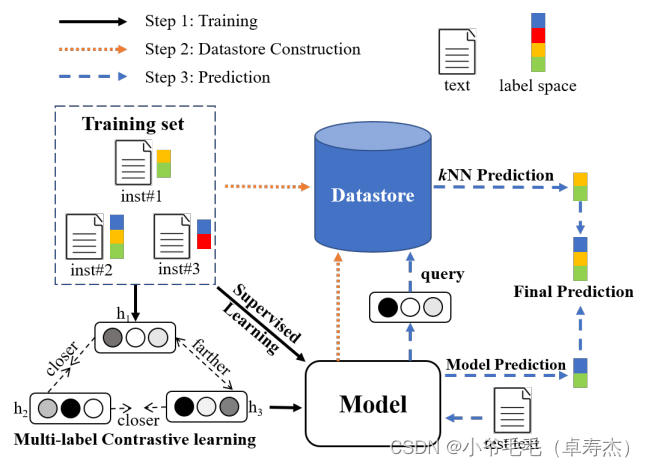
如上图所示,作者为MLTC设计了一个k个最近邻机制(步骤2,3),并通过使用多标签对比学习目标训练模型(步骤1)对其进行增强。
2.1 问题定义
设 D = { ( x i , y i ) } i = 1 N D = \{(x_i,y_i)\} ^N_{i=1} D={(xi,yi)}i=1N是由N个实例组成的MLTC训练集。每个 x i x_i xi都是一个文本, y i ∈ 0 , 1 L y_i∈{0,1}^ L yi∈0,1L为对应的 multi-hot 标签向量,其中L为标签总数。MLTC的目标是学习从输入文本到相关标签的映射。
2.2 最近邻MLTC
为了在推理过程中从现有实例中获取知识,作者提出了一个MLTC的k个最近邻机制,包括两个步骤:
- 构建训练实例的数据存储(步骤2):给定来自训练集 ( x i , y i ) ∈ D (x_i,y_i)∈D (xi,yi)∈D的一个实例,其文本表示向量 h i = f ( x i ) h_i = f(x_i) hi=f(xi)由一个MLTC模型生成。那么,训练实例的数据存储 D ‘ D` D‘可以通过通过每个训练实例离线构造: D ‘ = { ( h i , y i ) } i = 1 N D‘=\{(h_i,yi)\}^N_{i=1} D‘={(hi,yi)}i=1N。
- 基于训练实例的数据存储进行kNN预测(步骤3): 在推理阶段,给定一个输入文本x,模型输出预测向量
y
ˆ
M
o
∈
{
p
∣
p
∈
[
0
,
1
]
}
L
yˆ_{Mo}∈\{p|p∈[0,1]\} ^L
yˆMo∈{p∣p∈[0,1]}L。模型还输出文本表示
f
(
x
)
f (x)
f(x),用来查询数据存储D‘,根据欧氏距离获得k最近邻
N
=
(
h
i
,
y
i
)
i
=
1
k
N = {(h_i, y_i)}^k_{i=1}
N=(hi,yi)i=1k。然后可以进行kNN预测:
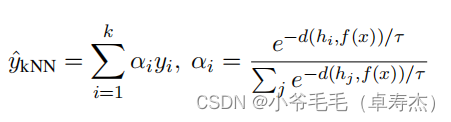
式中, d ( ⋅ , ⋅ ) d(·,·) d(⋅,⋅)为欧氏距离,τ为kNN温度, α i α_i αi为第i个相邻实例的权重。直观地说,一个相邻实例越接近测试实例,它的权重就越大。最终的预测是基础模型输出和kNN预测的组合: y ˆ = λ y ˆ k N N + ( 1 − λ ) y ˆ M o yˆ=λyˆ_{kNN}+(1−λ)yˆ_{Mo} yˆ=λyˆkNN+(1−λ)yˆMo,其中λ为比例参数。
笔者理解,在标签时常变更(下线、新增)的业务场景下,可以将λ设置为1.0,用单纯的kNN检索的方案。该方案好处在于,算对于标签的变更不能及时训练模型,也能支持在新标签体系下的预测。
2.3 多标签对比学习
在MLTC中,模型通常是通过二元交叉熵(BCE)损失的监督学习训练,而不知道kNN检索过程。因此,检索到的相邻实例可能没有与测试实例相似的标签,并且对预测几乎没有什么帮助。为了填补这一空白,作者提出用多标签对比学习目标来训练模型。
现有的监督对比学习方法试图缩小来自同一类的实例之间的距离,并将来自不同类的实例推开。然而,在MLTC中,有两个实例可能共享一些共同的标签,但也可能有一些对每个实例都是唯一的标签。如何处理这些案例是在MLTC中利用对比性学习的关键。因此,为了建模多标签实例之间的复杂相关性,作者设计了一个基于标签相似度的动态系数。
考虑一个大小为b的minibatch,作者定义一个函数来输出特定实例的所有其他实例:
g
(
i
)
=
{
k
∣
k
∈
{
1
,
2
,
⋅
⋅
⋅
,
b
}
,
k
=
i
}
g (i) = \{k|k∈\{1,2,···,b\},k = i\}
g(i)={k∣k∈{1,2,⋅⋅⋅,b},k=i} 。每个实例对
(
i
、
j
)
(i、j)
(i、j)的对比损失可以计算为:
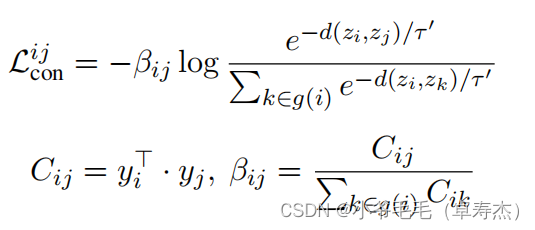
其中,
d
(
⋅
,
⋅
)
d(·,·)
d(⋅,⋅)为欧氏距离,τ‘为对比学习温度,
z
i
=
f
(
x
i
)
z_i = f(x_i)
zi=f(xi)表示文本表示。
C
i
j
C_{ij}
Cij表示i,j之间的标签相似度,由它们的标签向量的点积计算出来。动态系数
β
i
j
β_{ij}
βij是
C
i
j
C_{ij}
Cij的归一化处理。
对于一对实例 ( i , j ) (i,j) (i,j),标签相似度越大, C i j C_{ij} Cij的系数 β i j β_{ij} βij就越大,从而增加其损失项 L c o n i j L^{ij}_{con} Lconij的值。因此,它们的距离 d ( z i , z j ) d(z_i,z_j) d(zi,zj)将被优化为更接近。同时,如果它们没有共享的标签 ( β i j = C i j = 0 ) (β_{ij} = C_{ij} = 0) (βij=Cij=0),那么 L c o n i j L^{ij}_{con} Lconij的值也为零,它们的距离 d ( z i , z j ) d(z_i,z_j) d(zi,zj)将只出现在其他项的分母中。因此,它们的距离将有负的梯度,并被优化到更远。
将BCE损失表示为 L B C E L_{BCE} LBCE,作者的方法的总体训练损失为: L = L B C E + γ L c o n L = L_{BCE}+ γL_{con} L=LBCE+γLcon。参数γ控制了损失之间的权衡。
3. 实验效果

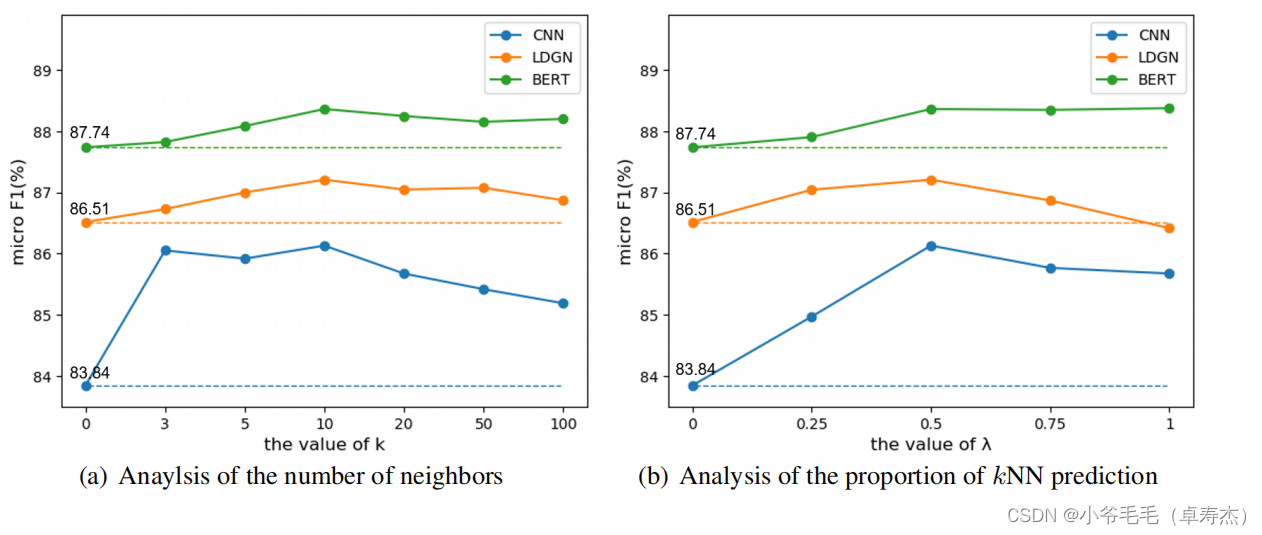
如上图所示,看到在不同的模型基础上该方案都有所提升。但如果是只做了对比学习,可能效果反而会下降。







![[iOS]UI分析工具Reveal](https://img-blog.csdnimg.cn/a6f8a08263a14d078cf050adb2aab1f8.png)