可上 欧弟OJ系统 练习华子OD、大厂真题
绿色聊天软件戳od1441了解算法冲刺训练(备注【CSDN】否则不通过)
文章目录
- 相关推荐阅读
- 一、题目描述
- 二、题目解析
- 三、参考代码
- Python
- Java
- C++
- 时空复杂度
- 华为OD算法/大厂面试高频题算法练习冲刺训练
相关推荐阅读
- Dijkstra算法的具体介绍详见单源最短路问题:Dijkstra算法详解【经典算法,限时免费】)
一、题目描述
题目链接:https://leetcode.cn/problems/network-delay-time/description/
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (u(i), v(i), w(i)),其中 u(i) 是源节点,v(i) 是目标节点, w(i) 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
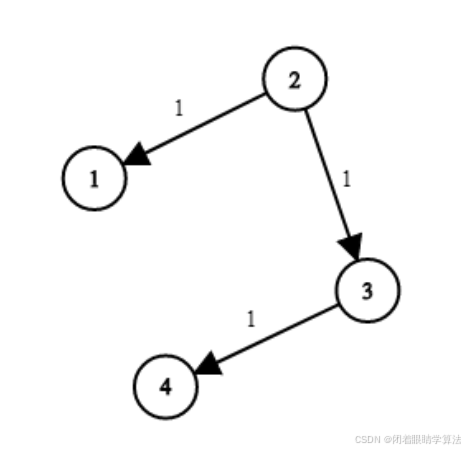
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= u(i), v(i) <= nu(i) != v(i)0 <= w(i) <= 100- 所有
(u(i), v(i))对都 互不相同(即,不含重复边)
二、题目解析
题目要求计算从源点出发到达所有其他节点的最短路径,在所有最短路径中找到最大值。
所以这是一个单源最短路问题,可以使用Dijkstra算法来解决,计算出dist数组之后取最大值即可。
Dijkstra算法的具体介绍详见单源最短路问题:Dijkstra算法详解【经典算法,限时免费】)
三、参考代码
Python
INF = 100000 # 用于表示一个非常大的数,作为初始的最短距离
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重
neighbor_dic = defaultdict(list)
for a, b, w in times:
# 将边 (a -> b) 和对应的权重 w 加入邻接表
neighbor_dic[a].append((b, w))
# 初始化一个列表 dist,用于记录从源节点 k 到每个节点的最短距离
# 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)
dist = [INF] * (n+1)
# 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点
# 堆中元素是 (当前时间, 当前节点) 元组
heap = [(0, k)]
# 进行Dijkstra(类似BFS)
while heap:
# 从堆中弹出当前时间最小的节点
cur_time, cur_node = heappop(heap)
# 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径
# 因此可以跳过当前节点
if cur_time > dist[cur_node]:
continue
# 更新从源节点 k 到当前节点的最短时间
dist[cur_node] = cur_time
# 遍历当前节点的所有相邻节点
for next_node, next_weight in neighbor_dic[cur_node]:
# 计算通过当前节点到达相邻节点所需的时间
next_time = cur_time + next_weight
# 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短
# 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索
if next_time < dist[next_node]:
heappush(heap, (next_time, next_node))
# 找到从源节点 k 到所有节点的最短路径中的最大值
ans = max(dist[1:])
# 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间
# 否则返回 -1,表示有节点无法到达
return ans if ans < INF else -1
Java
import java.util.*;
class Solution {
static final int INF = 100000; // 用于表示一个非常大的数,作为初始的最短距离
public int networkDelayTime(int[][] times, int n, int k) {
// 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重
Map<Integer, List<int[]>> neighbor_dic = new HashMap<>();
for (int i = 1; i <= n; i++) {
neighbor_dic.put(i, new ArrayList<>());
}
for (int[] time : times) {
int a = time[0], b = time[1], w = time[2];
// 将边 (a -> b) 和对应的权重 w 加入邻接表
neighbor_dic.get(a).add(new int[]{b, w});
}
// 初始化一个数组 dist,用于记录从源节点 k 到每个节点的最短距离
// 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[k] = 0; // 源节点到自己的距离为0
// 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点
// 堆中元素是 (当前时间, 当前节点) 元组
PriorityQueue<int[]> heap = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
heap.offer(new int[]{0, k});
// 进行Dijkstra(类似BFS)
while (!heap.isEmpty()) {
// 从堆中弹出当前时间最小的节点
int[] cur = heap.poll();
int cur_time = cur[0], cur_node = cur[1];
// 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径
// 因此可以跳过当前节点
if (cur_time > dist[cur_node]) {
continue;
}
// 遍历当前节点的所有相邻节点
for (int[] neighbor : neighbor_dic.getOrDefault(cur_node, new ArrayList<>())) {
int next_node = neighbor[0], next_weight = neighbor[1];
// 计算通过当前节点到达相邻节点所需的时间
int next_time = cur_time + next_weight;
// 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短
// 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索
if (next_time < dist[next_node]) {
dist[next_node] = next_time;
heap.offer(new int[]{next_time, next_node});
}
}
}
// 找到从源节点 k 到所有节点的最短路径中的最大值
int ans = Arrays.stream(dist).skip(1).max().getAsInt();
// 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间
// 否则返回 -1,表示有节点无法到达
return ans < INF ? ans : -1;
}
}
C++
int INF = 100000; // 用于表示一个非常大的数,作为初始的最短距离
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
// 创建一个邻接表,用于存储每个节点的相邻节点及对应的路径权重
unordered_map<int, vector<pair<int, int>>> neighbor_dic;
for (const auto& time : times) {
int a = time[0], b = time[1], w = time[2];
// 将边 (a -> b) 和对应的权重 w 加入邻接表
neighbor_dic[a].push_back({b, w});
}
// 初始化一个列表 dist,用于记录从源节点 k 到每个节点的最短距离
// 初始时,所有节点的距离都设置为 INF(表示尚未访问或不可达)
vector<int> dist(n + 1, INF);
dist[k] = 0; // 起点距离为0
// 初始化一个最小堆,用于在Dijkstra算法中提取当前已知最短路径的节点
// 堆中元素是 (当前时间, 当前节点) 元组
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
heap.push({0, k});
// 进行Dijkstra算法(类似BFS)
while (!heap.empty()) {
// 从堆中弹出当前时间最小的节点
auto [cur_time, cur_node] = heap.top();
heap.pop();
// 如果当前节点的已记录最短时间比当前时间更小,说明已经找到更优的路径
// 因此可以跳过当前节点
if (cur_time > dist[cur_node]) {
continue;
}
// 遍历当前节点的所有相邻节点
for (auto& [next_node, next_weight] : neighbor_dic[cur_node]) {
// 计算通过当前节点到达相邻节点所需的时间
int next_time = cur_time + next_weight;
// 如果通过当前节点到达相邻节点的时间比之前记录的最短时间更短
// 则更新相邻节点的最短时间,并将其加入堆中以便进一步探索
if (next_time < dist[next_node]) {
dist[next_node] = next_time;
heap.push({next_time, next_node});
}
}
}
// 找到从源节点 k 到所有节点的最短路径中的最大值
int ans = *max_element(dist.begin() + 1, dist.end());
// 如果最大值小于 INF,说明所有节点都可达,返回最大值作为网络延迟时间
// 否则返回 -1,表示有节点无法到达
return ans < INF ? ans : -1;
}
};
时空复杂度
时间复杂度:O((V+E)logV)。
空间复杂度:O(V+E)。
其中V是节点数,E是边数。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务300+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 大厂真题汇总 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多