贝叶斯推理：分步指南

一、说明

让我们深入了解贝叶斯推理的迷人世界。我将通过易于遵循的示例向您介绍其实际应用。贝叶斯推理为统计分析提供了一个强大而灵活的框架，特别是在存在不确定性和先验知识的情况下。通过结合先前的分布并使用贝叶斯定理根据新证据更新这些信念，贝叶斯方法使我们能够对未知参数做出更明智和细致的推断。

二、贝叶斯推理

要快速复习 MLE，您可以查看我的另一篇关于 MLE 的博客。

在讨论贝叶斯推理之前，让我们先讨论一下我们有什么，为什么我们需要任何新的东西——我们已经讨论了最大似然估计，以从一些已知数据（X）中估计未知量（θ）。
那么，MLE缺少什么——

MLE 处理的估计数量是恒定的。它试图找到使给定或观察到的数据（X）的可能性最大化的参数（θ）。

如果 θ 来自它自己的分布，那么如何合并它呢？

当 MLE 找到它为我们提供的参数时，点估计并不能量化与之相关的任何不确定性
MLE 倾向于使用复杂模型对数据进行过度拟合，尤其是在没有高估计参数的情况下。

对于从 X 估计 θ 的问题，我们讨论了一种特定方法，我们假设未知量 θ 是固定的。这种方法称为频率主义方法。为了克服MLE的缺点，我们需要一个不同的推理框架，即贝叶斯方法。在这个框架中，我们将参数 θ 视为来自分布 P（θ）的随机变量。这种分布 P（θ）称为先验分布。正如我们观察到的数据 X，我们将先验分布更新为后验分布，我们通过使用贝叶斯规则来做到这一点 —

直觉：
为了直观地了解贝叶斯推理让我们研究一个简单的问题
问：一天晚上，当你走进客厅时，你困惑地发现你的沙发是湿的。你必须扮演侦探，解开这一切是如何发生的谜团。
情况 1：也许你的弟弟全神贯注于他最喜欢的电视节目，在看电视时不小心把水洒了。
场景 2：一条淘气的鲨鱼，悄悄地潜入你的家，让沙发湿漉漉的。就像它看起来很神秘一样，鲨鱼在你回来时消失了。
那么，您认为是什么情况导致了沙发湿呢？
你可以很容易地理解，场景3与现实相去甚远，你的弟弟是罪魁祸首。但是，让我们借助概率概念来分析情景：

等一下，根据MLE，场景2是最合适的答案吗？但这没有任何意义。如果我们使用先验知识，即鲨鱼进入您房间的可能性太牵强了。

如果我们使用这些先验知识，那么

从这个简单的分析中，我们观察到，虽然最大似然估计（MLE）建议情景 3 是最可能的解释，但结合先前的信念会改变情景 2 的解决方案。这个修订后的解决方案更符合最初的直觉，而不是 MLE 解决方案。
该框架称为贝叶斯推理，涉及使用先验信息更新可能性，以得出修订后的概率，称为后验概率。

三、参数统计推断回顾：

让我们回顾一下统计推断问题的主要主题——

我们观察到了数据 X。
我们不知道生成 X 的概率分布。
我们定义了一个统计模型，即可能生成数据的概率分布。
我们使用参数 θ 对所提出的模型进行参数化。
我们使用数据 X 和模型来估计参数 θ。
我们做了一个关于数据生成分布的声明。

贝叶斯推理通过概率模型整合先验知识，扩展了参数方法。然后，我们使用贝叶斯定理更新我们的信念，这有助于我们将先前的知识与来自观察数据的新证据相结合。结果是一组后验分布，我们可以用来做出决策和得出结论。这种方法为我们提供了一种灵活而彻底的方法，在估计参数和做出决策时处理不确定性。

让我们一一讨论贝叶斯推理的构建块——

可能性：
参数贝叶斯推理的第一步是可能性，它是一个函数，简单地说给定参数 θ 看到数据 X 的概率是多少。

当数据生成分布的参数为 θ 时，似然等于 X 的 pdf。
示例 –假设从 N 次抛硬币中生成的样本为

X = [x1， x2， ⋯ ， xN] 其中习 = {0,1}。

由于数据是独立且相同分布的（IID），并且遵循伯努利分布。伯努利分布只有一个参数 μ Pdf 对于习样本是

我们可以将可能性写为：

先验分布：
        先验分布是分配给参数 θ 的概率分布。为了便于解释贝叶斯更新，我们使用共轭先验。
        如果似然函数 P（X|θ）和先验概率分布 P（θ）属于同一概率分布族，则产生的后验分布 P（θ|X）属于同一族。在这种情况下，我们将先验分布和后验分布称为相对于该可能性函数的共轭分布。
        示例 — 对于上一个示例，我们可以像之前一样使用 Beta 分发。

其中 α 和 β 是先验的参数。其中 α 表示成功，β表示失败。

后验分布：
我们使用来自数据 X 的信息，通过贝叶斯规则更新先验：

示例 —
继续上一个示例
：后置变为：

我们暂时不简化这个看起来很可怕的方程式，因为我们可以使用 MAP 估计从中估计μ。然而，通过检查它，我们可以掌握参数贝叶斯推理所必需的关键概念。

四、贝叶斯推理的一般思想

目的是通过观察给定的随机变量（数据）X 来推断有关未知变量（参数）θ 的信息。这些未知变量 θ 与先验分布有关，

在观察 X 的值后，我们找到了 θ 的后验分布。这是给定 X = x 的 θ 的条件 pdf（或 pmf）。

可以使用贝叶斯规则找到后验分布。

4.1 示例

让我们通过一些示例来理解所有概念：

示例 1
抛硬币数据 X 为 [1,1,1,1,1,1,1,1,0,0,0]。我们需要找到参数 θ = P（X = 1）
解决方案：
参数：θ = P（X = 1）
数据：X = [1,1,1,1,1,1,1,0,0,0] 其中 1 表示正面，0 表示尾部。
先前：由于我们对 θ 一无所知，因此我们可以假设 θ 来自均匀分布。

事先分发

可能性：每个样本都遵循伯努利分布，并遵循 IID 假设。

可能性

后验分布：通过使用贝叶斯规则，我们得到了后验分布，

后部分布

θ 的后验分布： f（θ|X）

示例 2 ：
实值数据 X 为 — [66.75,70.24,67.19,67.09,63.65,64.64,69.81,69.79,73.52,71.74]
，并且总体标准差是已知的并且值为 3，我们需要找到参数 μ = Ε（X）。
解：
参数： μ = ε（X）
数据： X = [66.75,70.24,67.19,67.09,63.65,64.64,69.81,69.79,73.52,71.74] 先前： 假设我们认为 θ 的平均值是 60，标准差为 5。

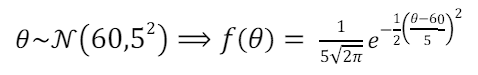
事先分发

可能性： 每个样本都遵循正态分布，并保持 IID 假设

可能性

后验分布：通过使用贝叶斯规则，我们得到了后验分布，

后部分布

经过一些操作，我们可以得到，（它太长了）

后部分布

θ 的后验分布： f（θ|X）

4.2 迭代学习

通过使用贝叶斯框架，我们可以开发一个迭代学习系统。让我们看看如何做到这一点：

从关于参数 θ 的先验知识开始，即 θ~P（θ）
通过使用贝叶斯规则合并观测数据 X，将先前的 P（θ）更新为后 P（θ|X）。

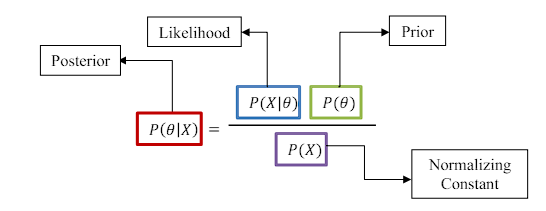
然后将后验设置为先验，并使用新的观测数据 Y 更新它并继续。这称为顺序贝叶斯推理。

五、结论

总之，贝叶斯推理为统计分析提供了一个强大而灵活的框架，特别是在存在不确定性和先验知识的情况下。通过结合先前的分布并使用贝叶斯定理根据新证据更新这些信念，贝叶斯方法使我们能够对未知参数做出更明智和细致的推断。这种方法不仅解决了 MLE 等传统方法的局限性，而且还提供了一种全面的概率理解，这对于在面对不确定性时做出稳健的决策至关重要。随着我们在计算能力上的不断进步，贝叶斯推理的应用和相关性可能会增长，为我们在各个研究领域提供更深入的见解。