Differentiable Model Scaling(DMS)以直接、完全可微的方式对宽度和深度进行建模,是一种高效且多功能的模型缩放方法。与先前的NAS方法相比具有三个优点:1)DMS在搜索方面效率高,易于使用。2)DMS实现了高性能,可与SOTA NAS方法相媲美。3)DMS是通用的,与各种任务和架构兼容。来源:晓飞的算法工程笔记 公众号
论文: Differentiable Model Scaling using Differentiable Topk

- 论文地址:https://arxiv.org/abs/2405.07194
Introduction
在近年来,像GPT和ViT这样的大型模型展示了出色的性能。值得注意的是,GPT-4的涌现强调了通过扩展网络来实现人工通用智能(AGI)的重要性。为了支持这个扩展过程,论文引入了一种通用而有效的方法来确定网络在扩展过程中的最佳宽度和深度。
目前,大多数网络的结构设计仍然依赖于人类专业知识。通常需要大量资源来调整结构超参数,导致很难确定最佳结构。与此同时,神经架构搜索(NAS)方法已经被引入到自动化网络结构设计中。根据搜索策略将NAS方法分为两类:随机搜索方法和基于梯度的方法。
随机搜索方法需要对大量子网络进行采样以比较性能。然而,这些方法的搜索效率受到样本评估周期的限制,导致性能降低和搜索成本增加。
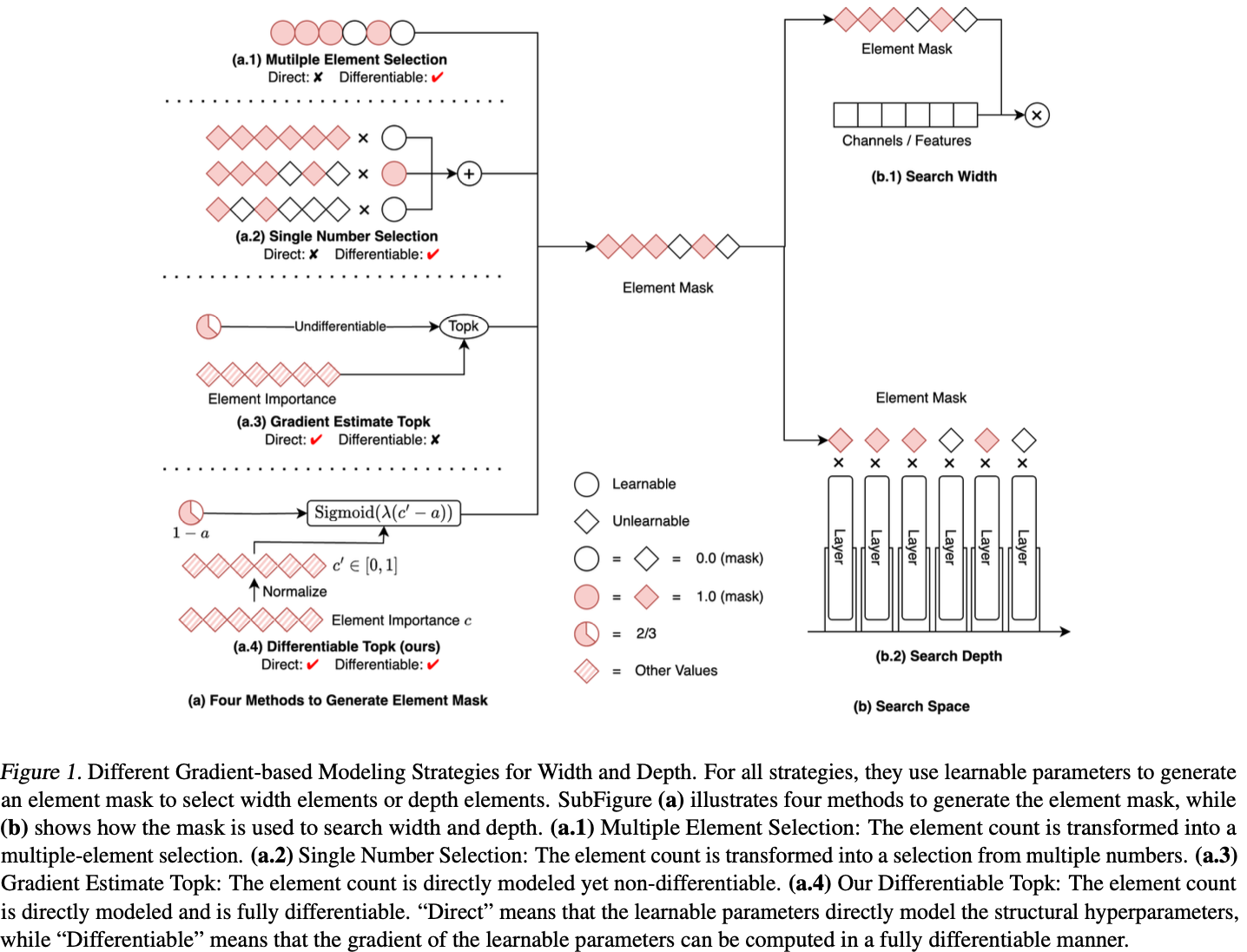
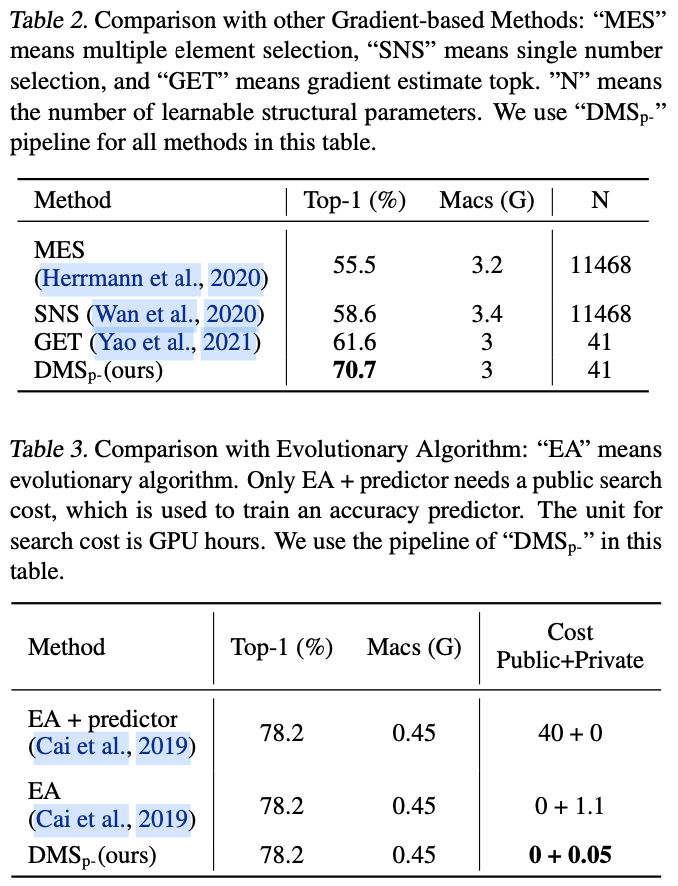
与随机搜索方法不同,基于梯度的方法采用梯度下降法来优化结构参数、 提高效率,使其更善于平衡搜索成本和最终性能。然而,一个巨大的挑战依然存在:如何以直接和可微的方式为结构超参数建模?早期的方法一直在努力应对这一挑战,结果导致性能下降、成本增加。具体来说,根据建模策略将先前的方法分为三类:
- 多元素选择:在搜索卷积层中的通道数时,将通道数建模为通道选择(比如
PaS通过可学习二值卷积生成0/1掩码对通道进行剪枝),如图1 a.1所示。 - 单数字选择:在搜索卷积层中的通道数时,将通道数建模为从多个候选数字中的选择一个(比如
FBNetV2在一层中学习不同大小的候选卷积的权重),如图1 a.2所示。 - 梯度估计
topk:尝试直接建模宽度和深度(比如通过梯度估计学习动态的k值以及给每个通道生成重要性分数,随后选择topk通道),如图1 a.3所示。这个可能跟多元素选择有点类似,核心区别是多元素选择是为了生成掩码,而这个则是为了生成动态k值。
但所有上述策略都无法以直接和完全可微分的方式对结构超参数进行建模。为了解决上述挑战,论文引入了一个完全可微分的topk运算符,可以无缝地以直接和可微分的方式对深度和宽度进行建模。值得注意的是,每个可微分的topk运算符都有一个可学习参数,表示深度或宽度结构超参数,可以基于任务损失和资源约束损失的指导进行优化。与现有的基于梯度的方法相比,论文的方法在优化效率方面表现出色。
基于可微分topk,论文提出了一种可微分模型缩放(DMS)算法来搜索网络的最佳宽度和深度。为了验证功效和效率,在各种任务中进行了严格的测试,包括视觉任务和NLP任务,以及不同的架构,包括CNN和Transformer。由于可微分topk具有高效的搜索效率,DMS在性能或搜索成本方面均优于先前的SOTA方法。
总的来说,论文的贡献如下:
- 引入了可微分的
topk运算符,可以以直接和可微分的方式对结构超参数进行建模,因此很容易进行优化。 - 基于可微分的
topk提出了一种可微分模型缩放(DMS)算法,用于搜索网络的最佳宽度和深度。 - 评估了
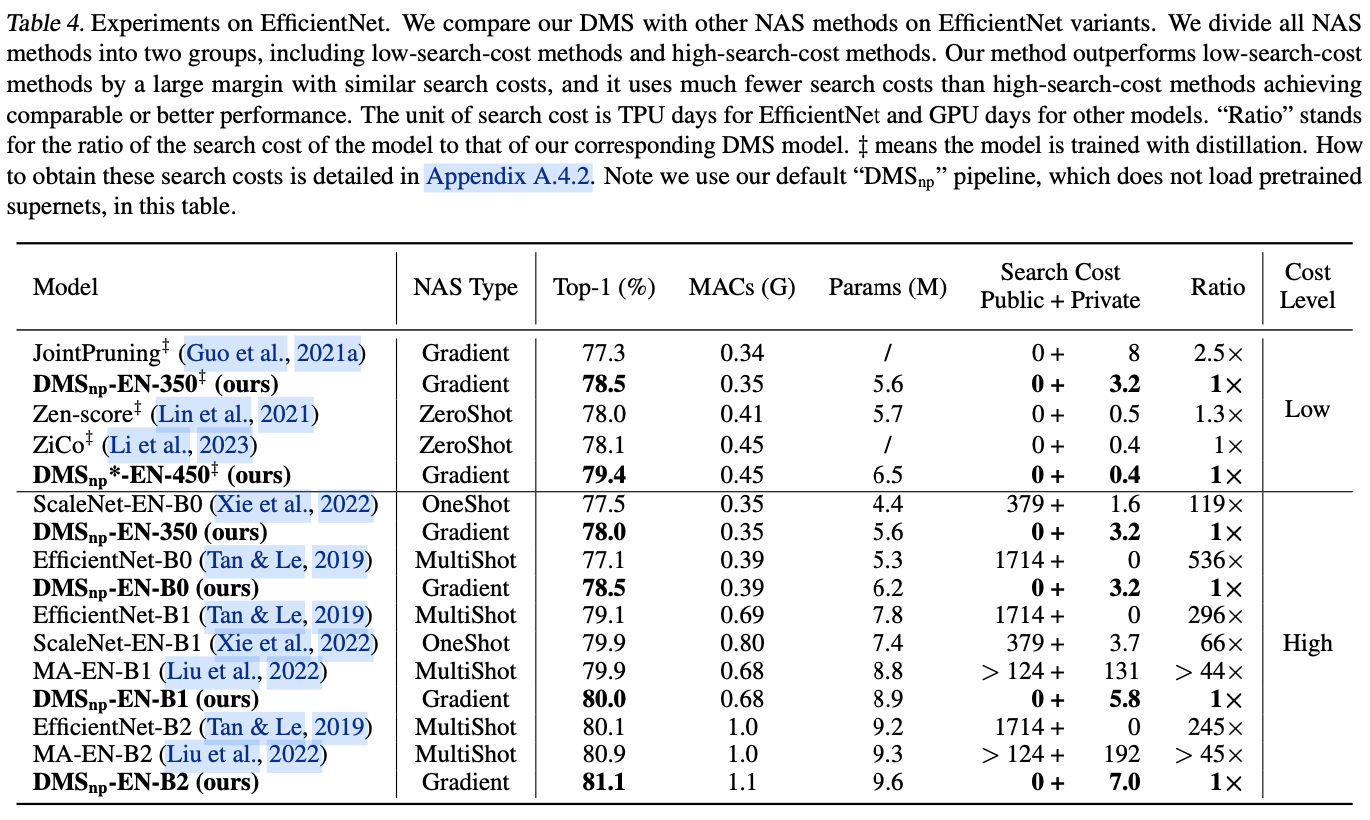
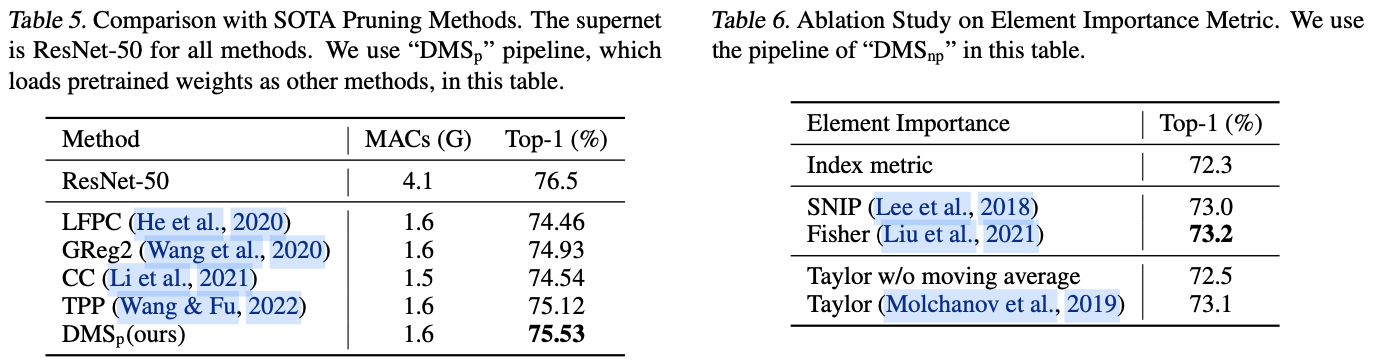
DMS在各种任务和架构上的性能。例如,DMS在搜索过程中只需0.4 GPU天,就能比最先进的zero-shot NAS方法ZiCo表现出1.3%的优势。与性能相当的one-shot NAS方法ScaleNet以及multi-shot NAS方法Amplification相比,DMS所需的搜索成本仅为几十分之一。此外,DMS是一种广泛适用的方法,在COCO数据集上将Yolo-v8-n的提高了2.0%,并提高了裁剪Llama-7B模型样本分类精度。
Related Work
Stochastic Search Methods
随机搜索方法通常通过采样和评估的循环过程进行操作。在每一步中,它们会对具有不同构的模型进行采样,然后对其进行评估。这种策略非常灵活,可以处理连续和离散的搜索空间。然而,它的一个显著缺点搜索效率低下,导致资源消耗高和性能不理想。具体而言,基于随机搜索的方法可以分为三种:
multi-shot NAS:需要训练多个模型,这非常耗时,如EfficientNet用了1714个TPU天来进行搜索。one-shot NAS:需要训练一个庞大的超网络,也需要大量资源,如ScaleNet用了379个GPU天来训练一个超网络。zero-shot NAS:通过消除训练任何模型来减少成本,但其性能尚未达到所期望的标准。
Gradient-based Methods
基于梯度的结构搜索方法使用梯度下降来探索模型的结构,这些方法一般比随机搜索方法更高效。基于梯度的方法的关键在于如何使用可学习参数来建模结构超参数并计算其梯度,理想情况下,可学习参数应直接建模结构超参数并且其梯度应以完全可微的方式计算。然而,先前的方法在建模网络的宽度和深度时往往难以同时满足这两个条件,可以将它们分为三类:(1)多元素选择,(2)单数字选择和(3)梯度估计topk。前两类间接地建模结构超参数,而第三类不可微分,需要进行梯度估计。
为了提高结构搜索的优化效率,论文引入了一种新的可微分的topk方法,可以直接建模宽度和深度,并且是完全可微分的。从实验结果来看,论文的方法更加高效和有效。
Method
Differentiable Top-k
假设存在一个由
k
k
k 表示的结构超参数,表示元素的数量,比如卷积层中的
k
k
k 个通道或网络阶段中的
k
k
k 个残差块。
k
k
k 的最大值为
N
N
N,使用
c
∈
R
N
{\mathbf{c}} \in \mathbb{R}^N
c∈RN来表示元素的重要性,其中较大的值表示更高的重要性。可微分topk方法的目标是输出一个软掩码
m
∈
0
,
1
N
{\mathbf{m}} \in 0,1^N
m∈0,1N,代表具有前
k
k
k 个重要分数的选定元素。
topk运算符使用可学习的参数
a
a
a 作为阈值,选择那些重要性值大于
a
a
a 的元素。
a
a
a 能够直接建模元素数量
k
k
k,因为
k
k
k 可以看作是
a
a
a 的一个函数,其中
k
=
∑
N
_
i
=
1
1
c
_
i
>
a
k=\sum^N\_{i=1}{1c\_i>a}
k=∑N_i=11c_i>a。
1
A
1A
1A 是一个指示函数,如果
A
A
A 为真则等于1,否则等于0,
c
_
i
c\_i
c_i 表示第
i
i
i 个元素的重要性。将topk表示为一个函数
f
f
f,如下所示:
m _ i = f ( a ) ≈ { 1 if c _ i > a 0 otherwise \begin{align} m\_i = f(a) \approx \begin{cases} 1 & \text{if } c\_i > a \ 0 & \text{otherwise} \end{cases} \end{align} m_i=f(a)≈{1if c_i>a 0otherwise
在先前的方法中, f f f 通常是一个分段函数,不平滑也不可微分,且 a a a 的梯度是通过估计计算得出的。论文认为采用相对于 a a a 完全可微分的 f f f 的最大挑战是重要性分数分布不均匀。具体来说,不均匀的分布导致重要性值排序中的两个相邻元素之间的差异较大。假设每次迭代时通过固定值更新 a a a,当前后元素的重要性差异很大时,则需要许多步才能使 a a a 跨越这两个元素。当差异很小时, a a a 可以在一步内跨越许多元素。因此,在元素重要性不均匀时,以完全可微分的方式优化 a a a 是非常困难。
为了解决这个挑战,论文采用了一种重要性归一化过程,将不均匀分布的重要性强制转换为均匀分布的值,使得topk函数在可微分的情况下变得平滑且易于优化。总结起来,可微分topk有两个步骤:重要性归一化和软掩码生成。
Importance Normalization
根据以下方式,通过将所有元素的重要性映射到从0到1的均匀分布的值来对所有元素的重要性归一化:
c i ′ = 1 N ∑ j = 1 N 1 c _ i > c _ j . \begin{align} & c_i' = \frac{1}{N}\sum^N_{j=1}{1c\_i>c\_j}. \end{align} ci′=N1j=1∑N1c_i>c_j.
归一化后的元素重要性用
c
′
{\mathbf{c}}'
c′ 表示。
1
A
1A
1A 是与上面相同的指示函数,
c
{\mathbf{c}}
c 中的任意两个元素通常是不同的。值得注意的是,虽然
c
′
\mathbf{c}'
c′ 在0到1之间均匀分布,但
c
\mathbf{c}
c 可以遵循任何分布。
直观地说, c ′ _ i c'\_i c′_i 表示 c {\mathbf{c}} c 中值小于 c _ i c\_i c_i 的部分。此外,可学习的阈值 a a a 也变得有意义,表示元素的剪枝比例。 k k k 可以通过 k = ⌊ ( 1 − a ) N ⌉ k=\lfloor(1-a)N\rceil k=⌊(1−a)N⌉ 计算,其中 ⌊ ⌉ \lfloor \, \rceil ⌊⌉ 是一个取整函数。 a a a 限制在 0 , 1 0,1 0,1 的范围内,其中 a = 0 a=0 a=0 表示不剪枝, a = 1 a=1 a=1 表示剪枝所有元素。
Soft Mask Generation
在归一化之后,可以使用基于相对大小的剪枝比例 a a a 和归一化元素重要性 c ′ {\mathbf{c}}' c′的平滑可微函数轻松生成软掩码${\mathbf{m}} $。
m _ i = f ( a ) = Sigmoid ( λ ( c ′ _ i − a ) ) = 1 1 + e − λ ( c ′ _ i − a ) . \begin{align} & m\_i = f(a)= \text{Sigmoid}(\lambda({\mathbf{c}}'\_i- a)) = \frac{1}{1+e^{-\lambda({\mathbf{c}}'\_i - a)}}. \end{align} m_i=f(a)=Sigmoid(λ(c′_i−a))=1+e−λ(c′_i−a)1.
论文添加了一个超参数
λ
\lambda
λ来控制从公式3到硬掩码生成函数的逼近程度。当
λ
\lambda
λ趋近于无穷大时,公式3接近于硬掩码生成函数(根据固定阈值
a
a
a 直接得出0/1)。通常将
λ
\lambda
λ设置为
N
N
N,因为当
c
′
_
i
>
a
+
3
/
N
c'\_i>a+3/N
c′_i>a+3/N或
c
′
_
i
<
a
−
3
/
N
c'\_i<a-3/N
c′_i<a−3/N时,$|(m_i-\lfloor m_i \rceil)|<0.05 $。这意味着除了重要性值接近剪枝比例的六个元素外,其他元素的掩码接近于0或1,近似误差小于0.05。因此,
λ
=
N
\lambda=N
λ=N足以逼近topk的硬掩码生成函数。
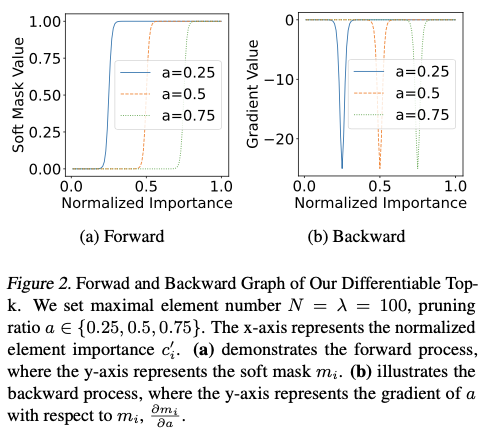
公式3的前向和反向图分别如图2(a) 和图2(b) 所示,可以观察到以下两点:
topk直接使用可学习的剪枝比例 a a a 来建模元素数量 k k k,并在前向过程中生成极化的软掩码 m {\mathbf{m}} m,以完美模拟剪枝后的模型。- 可微分
topk完全可微分,并且能够稳定地进行优化。 a a a相对于 m i m_i mi的梯度为 $\frac{\partial m_i}{\partial a} = -\lambda(1-m_i)m_i $。我们的__topk直观地检测模糊区域中 0.05 < m _ i < 0.95 0.05<m\_i<0.95 0.05<m_i<0.95的掩码梯度。请注意,图2__(b) 描述的是 ∂ m _ i ∂ a \frac{\partial m\_i}{\partial a} ∂a∂m_i的值,而不是 a a a 的总梯度, a a a 的总梯度为 ∑ i = 1 N ∂ t a s k _ l o s s ∂ m _ i ∂ m _ i ∂ a + ∂ r e s o u r c e _ l o s s ∂ a \sum_{i=1}^{N}{\frac{\partial task\_loss}{\partial m\_i}\frac{\partial m\_i}{\partial a}}+\frac{\partial resource\_loss}{\partial a} ∑i=1N∂m_i∂task_loss∂a∂m_i+∂a∂resource_loss。
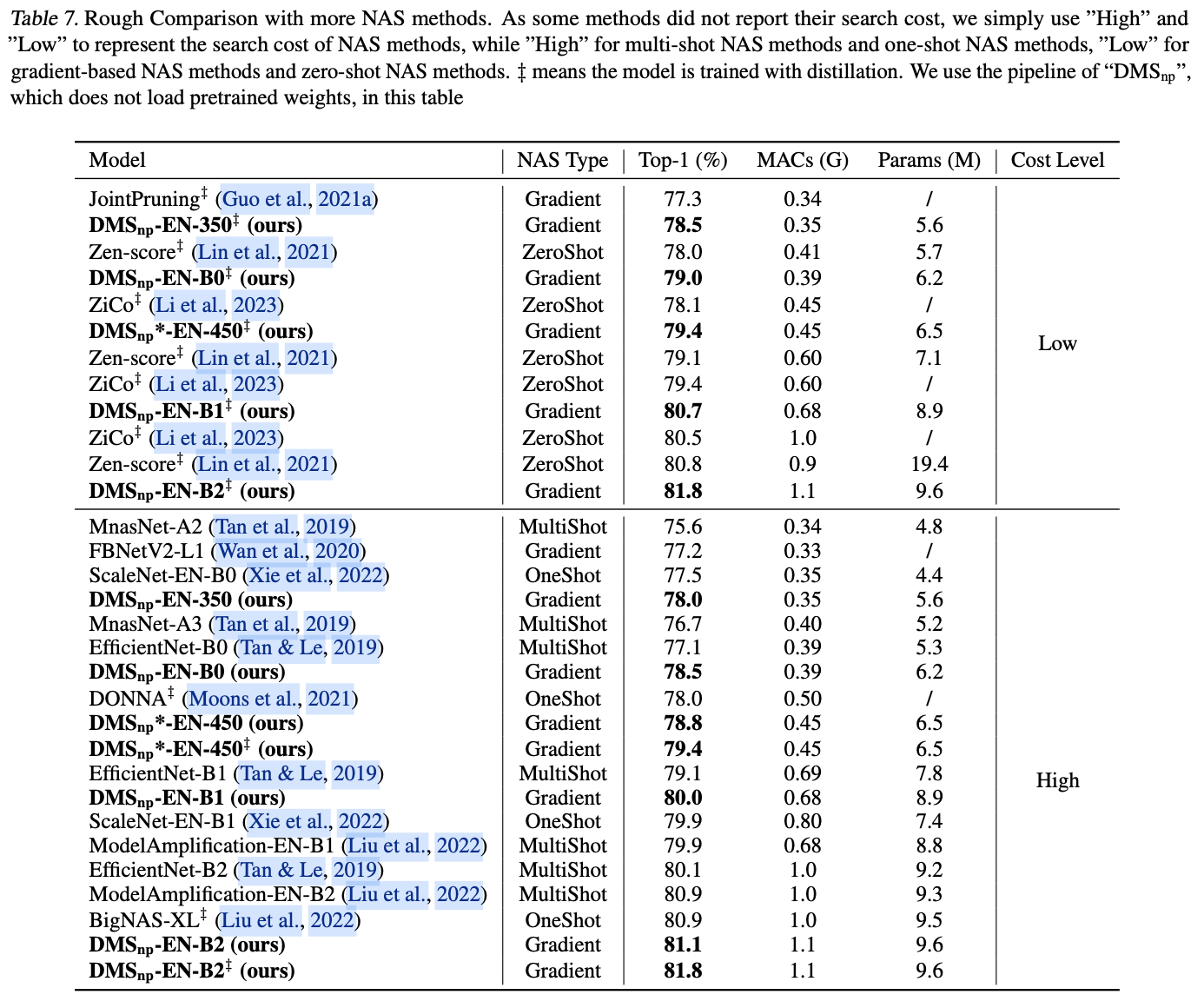
Element Evaluation
由于元素重要性会被归一化后再进行掩码生成,所以不限制元素重要性的分布,可以通过多种方法来量化元素重要性,例如L1-norm 等。论文以滑动平均方式实现了Taylor importance,具体如下所示:
c i t + 1 = c t _ i × d e c a y + ( m t _ i × g i ) 2 × ( 1 − d e c a y ) . \begin{align} c^{t+1}_i = c^t\_i \times decay + (m^t\_i \times g_{i})^2 \times (1-decay). \end{align} cit+1=ct_i×decay+(mt_i×gi)2×(1−decay).
在这里,
t
t
t表示训练步骤,
g
_
i
g\_i
g_i 是
m
_
i
m\_i
m_i 相对于训练损失的梯度,
D
e
c
a
y
Decay
Decay是衰减率,
c
_
i
0
c\_i^0
c_i0的初始值设为零,衰减率设为0.99。请注意,元素的重要性不是通过梯度下降来更新的。通过利用Taylor importance,可以高效且稳定地估计元素的重要性。
Differentiable Model Scaling
依靠可微分topk,论文提出了可微分模型缩放(Differentiable Model Scaling,DMS)来优化网络的宽度和深度。DMS有三种基于基于训练的模型剪枝的流水线变体,如表1所示。
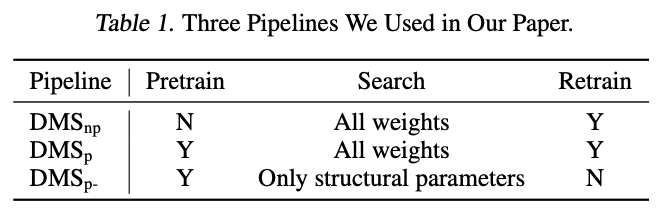
- DMS _ p \text{DMS}\_{\text{p}} DMS_p
DMS _ p \text{DMS}\_{\text{p}} DMS_p 是基于训练的模型剪枝流水线,由预训练阶段、搜索阶段和重新训练阶段组成:
- 预训练阶段用于预训练一个超网络,通常需要大量时间和资源。
- 搜索阶段在特定资源约束下搜索超网络的最优宽度和深度,由于论文方法具有较高的搜索效率,因此搜索阶段只使用了大约
1/10或更少的重新训练轮数。 - 在重新训练阶段,重新对已经进行了搜索的模型进行训练。与
SOTA剪枝方法进行比较时,使用这个流水线。 - DMS _ np \text{DMS}\_{\text{np}} DMS_np
DMS
np
\text{DMS}_{\text{np}}
DMSnp 是论文中默认和最常用的流水线。预训练阶段的高本占据了总成本的大部分,这是__NAS__和剪方法在实际应用中面临的一个重大障碍。为克服这个问题,从
DMS
\text{DMS}_{\text{}}
DMS 中去除了预训练阶段,直接从随机初始化超网络开始搜索。通过增加超网络大小,
DMS
np
\text{DMS}_{\text{np}}
DMSnp 在性能和效率上都超过了
DMS
p
\text{DMS}_{\text{p}}
DMSp,并且比其他NAS方法更加高效。
- DMS _ p- \text{DMS}\_{\text{p-}} DMS_p-
DMS
p-
\text{DMS}_{\text{p-}}
DMSp- 用于快速比较不同搜索方法。与
DMS
p
{\text{DMS}_\text{p}}
DMSp 相比,它只优化结构参数,不对搜索到的模型进行重新训练。利用现有的预训练超网络,也能输出合理的结果。此外,它只需要数百次迭代,在单个RTX3090上花费不到10分钟就可以搜索出一个模型。
- Search Space
如图1(b)所示,论文的搜索空间涵盖了网络的宽度和深度,这是模型扩展最关键的结构超参数。为了表示这些维度,使用了可微分的topk方法。在网络中,宽度通常涵盖了卷积层中的通道维度、全连接层中的特征维度等。关于深度,论文专注于具有残差连接的网络,并搜索每个阶段中的块数。具体来说,将可微分topk的软掩码合并到残差连接中,使得每个块可以表示为
x
_
i
+
1
=
x
_
i
+
f
(
x
_
i
)
×
m
_
i
x\_{i+1}=x\_i+f(x\_i)\times m\_i
x_i+1=x_i+f(x_i)×m_i。
此外,对于结构超参数
x
x
x,在范围
1
,
x
_
m
a
x
1, x\_{max}
1,x_max 内以步长1进行搜索,而大多数先前的NAS方法则在范围
x
m
i
n
,
x
m
a
x
x_{min}, x_{max}
xmin,xmax 内以步长32进行搜索。这个搜索空间是由人类专家设计的一个较好的子空间,然而论文的搜索空间更加通用且成本最低。实验结果显示,论文的方法在精细搜索空间上可以达到更好的性能,这个空间更难搜索,而先前的方法在粗粒度搜索空间上的表现较好,这种空间更容易搜索。
- Resource Constraint Loss
为了确保网络遵循特定的资源约束,在优化过程中加入了一个额外的组件,称为Resource Constraint Loss。因此,整体的损失函数为:
l o s s = l o s s t a s k + λ r e s o u r c e × l o s s _ r e s o u r c e . l o s s _ r e s o u r c e = { log ( r c r t ) if r c > r t 0 otherwise . \begin{align} loss= & loss_{task}+\lambda_{resource}\times loss\_{resource}. \ & loss\_{resource}=\begin{cases} \log(\frac{r_{c}}{r_{t}}) & \text{if } r_{c} > r_{t} \ 0 & \text{otherwise} \end{cases}. \end{align} loss=losstask+λresource×loss_resource. loss_resource={log(rtrc)if rc>rt 0otherwise.
在这里,
l
o
s
s
t
a
s
k
loss_{task}
losstask 表示任务损失。
l
o
s
s
r
e
s
o
u
r
c
e
loss_{resource}
lossresource 表示额外的资源约束损失,
λ
_
r
e
s
o
u
r
c
e
\lambda\_{resource}
λ_resource 作为其权重系数。
r
r
r 表示当前资源消耗水平,根据可学习参数的不同topk操作符进行计算。
r
_
t
r\_t
r_t 代表目标资源耗水平,由用户指定。由于topk是完全可微分的,可学习结构参数可以在任务损失和资源约束失的指导下进行优化。
Experiment
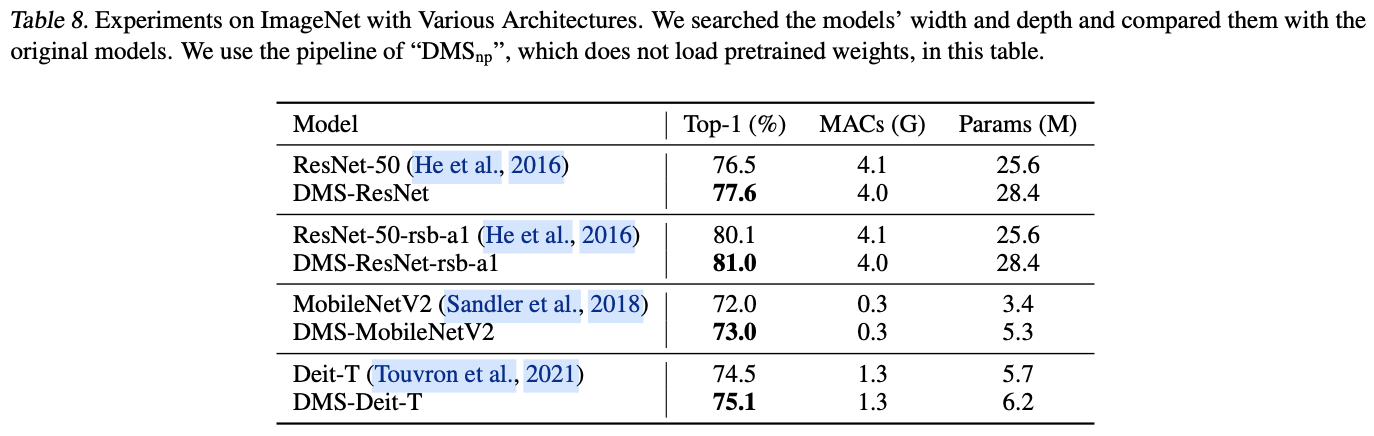

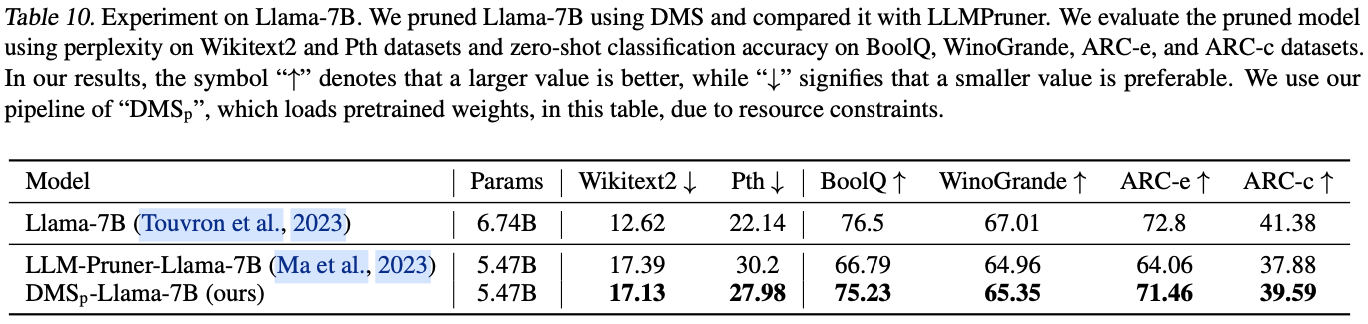
如果本文对你有帮助,麻烦点个赞或在看呗
更多内容请关注 微信公众号【晓飞的算法工程笔记】

















![HTML+CSS+JS实现商城首页[web课设代码+模块说明+效果图]](https://i-blog.csdnimg.cn/direct/41f0acdef9e64987abfa53283973f387.png)