【myz_tools】Python库 myz_tools：Python算法及文档自动化生成工具

文章目录

0.2.0 更新内容如下
- - - 函数generate_2d_combinations_iter
    - 函数generate_row_permutations
    - 函数calculate_total_permutations
    - 函数display_combinations
    - 函数evaluate_list_similarity
    - 函数check_unique
写在前面
关于库
库使用
库内所有函数目录
文件名称: common_maths.py
- 函数部分：
- - - 函数create_dir
    - 函数get_max_diff
    - 函数remove_outliers_iqr
    - 函数export_to_csv
    - 函数generate_2d_combinations_iter
    - 函数generate_row_permutations
    - 函数calculate_total_permutations
    - 函数display_combinations
    - 函数evaluate_list_similarity
    - 函数check_unique
文件名称: source2md.py
- 函数部分：
- - - 函数dir2md
    - 函数extract_info
    - 函数all_save_markdown
    - 函数all2md
    - 函数extract_function_docs_from_file
    - 函数save_docs_to_markdown
    - 函数pyFun2md
仓库的链接
END

0.2.0 更新内容如下

增加了6个函数

更新内容如下

函数generate_2d_combinations_iter

功能：
    传入一个三维数组，返回每个二维数组的所有元素组合的迭代器。如果设置了 `test_first_group` 参数True,
    则仅返回第一个二维数组的组合。

参数：
    data_3d (list): 一个三维列表，每个元素都是一个二维列表，表示多个二维数组。
    test_first_group (bool): 是否只生成第一个二维数组的组合。默认为 False。

返回值：
    generator: 一个生成器对象，按需生成每个二维数组的所有元素组合。

异常：
    ValueError: 如果输入的数据不是三维列表，则抛出异常。

示例：
    >>> data = [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]
    >>> result_iter = generate_2d_combinations_iter(data)
    >>> for combinations in result_iter:
            # 每次拿到是一个二维列表的组合
    ...     print(list(combinations)) # [(1, 3), (1, 4), (2, 3), (2, 4)]
    下一次
    [(5, 7), (5, 8), (6, 7), (6, 8)]


    >>> result_iter = generate_2d_combinations_iter(data, test_first_group=True)
    >>> print(list(next(result_iter)))
    [(1, 3), (1, 4), (2, 3), (2, 4)]

函数generate_row_permutations

功能：
    传入一个二维数组，返回该二维数组中每一行元素所有可能的排列组合。


参数：
    data_2d (list): 一个二维列表，表示多个行数据。

返回值：
    generator: 生成器对象，按需生成每一行的所有排列组合并组合成二维数组。

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> permutations = generate_row_permutations(data)
    >>> for perm in permutations:
    ...     print(perm)
    [[1, 2], [3, 4]]
    [[1, 2], [4, 3]]
    [[2, 1], [3, 4]]
    [[2, 1], [4, 3]]

函数calculate_total_permutations

功能：
    计算并返回二维数组中所有行的排列组合总数。

参数：
    data_2d (list): 一个二维列表，表示多个行数据。

返回值：
    int: 所有行排列组合的总数。

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> total = calculate_total_permutations(data)
    >>> print(total)
    4

函数display_combinations

功能：
    打印二维数组中前 N 个排列组合，以检测组合生成的正确性。

参数：
    data_2d (list): 一个二维列表，表示多个行数据。
    N (int): 要打印的组合数量，默认为 5。

返回值：
    None

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> display_combinations(data, N=2)
    [1, 2]
    [3, 4]

    [1, 2]
    [4, 3]

函数evaluate_list_similarity

evaluate_list_similarity 函数的各个评分方法都可以理解为“分数越小越好”的形式。

均方误差 (MSE)：
- 公式: $\text{MSE} = \frac{1}{m} \sum_{i=1}^{m} (d_i - n)^2$
- 解释: 计算所有差值与目标值 n 的平方差的平均值。均方误差对较大的差异惩罚更严重，得分越小表示列表元素与目标值的接近程度越高。
平均绝对误差 (MAE)：
- 公式: $\text{MAE} = \frac{1}{m} \sum_{i=1}^{m} |d_i - n|$
- 解释: 计算所有差值与目标值 n 的绝对差的平均值。与均方误差相比，平均绝对误差对所有差异的惩罚是均等的。得分越小表示列表元素与目标值的接近程度越高。
总分 (Total Score)：
- 公式: $\text{Total Score} = \sum_{i=1}^{m} |d_i - n|$
- 解释: 计算所有差值与目标值 n 的绝对差的总和。总分直接反映了所有差异的累积程度。得分越小表示列表元素与目标值的接近程度越高。

功能：
    评估列表中元素间的差异与给定值 `n` 的接近程度。支持不同的评分方法，例如均方误差 (MSE)、绝对误差等。
    三种方式都是得分越小表示列表元素与目标值的接近程度越高
参数：
    lst (list of int/float): 需要评估的数字列表。
    n (int/float): 用于比较的参考值，计算差异的目标值。
    method (str): 选择的评分方法。支持 'MSE'（均方误差）、'MAE'（平均绝对误差）、'total_score'（总分）等。

返回值：
    float: 计算得出的评分值。

异常：
    ValueError: 如果输入的 `lst` 不是列表或 `n` 不是整数或浮点数，则抛出异常。
    TypeError: 如果 `lst` 中的元素不是整数或浮点数，则抛出异常。
    ValueError: 如果选择的评分方法不被支持，则抛出异常。

示例：
    >>> lst = [1, 3, 6, 10]
    >>> n = 2
    >>> score = evaluate_list_similarity(lst, n, method='MSE')
    >>> print(score)

    >>> score = evaluate_list_similarity(lst, n, method='MAE')
    >>> print(score)

函数check_unique

功能：
    检查传入的二维数组中的每个元素是否都是唯一的。如果所有元素唯一，返回 True；否则，返回 False。

参数：
    data (list of list): 一个二维列表，其中包含需要检查的元素。

返回值：
    bool: 如果所有元素都唯一，返回 True；否则，返回 False。

异常：
    TypeError: 如果输入的 `data` 不是一个二维列表，或包含非列表的元素，则抛出异常。

示例：
    >>> data = [[1, 2, 3], [4, 5, 6]]
    >>> check_unique(data)
    True

    >>> data = [[1, 2, 3], [3, 4, 5]]
    >>> check_unique(data)
    False

写在前面

本来最开始只是单纯的想整理一下常用到的各类算法，还有一些辅助类的函数，方便时间短的情况下快速开发。后来发现整理成库更方便些，索性做成库，通过pip install 直接可以安装使用

关于库

平时见到的各类算法大多数还是需要自己手动敲，比如四分位距法，还得知道了原理后详改代码，索性直接做成函数，直接传入原始数据，返回清洗后的数据。内部的话代码也已经开源，也做过几轮测试，所以不用担心会出现什么奇奇怪怪的BUG之类，当然如果有的话还请提出

库使用

安装方式

pip install myz_tools

安装后就能用

目前主要两部分，一个算法，一个是用于python文件转化为文档的函数，使用也很方便，支持自定义目录和指定输出到一个md或者各自转化的不同的md文件里面，虽然有Sphinx可以用，但是我还是期待可以找到一种更加简洁的方式快速解决问题

使用方式如下

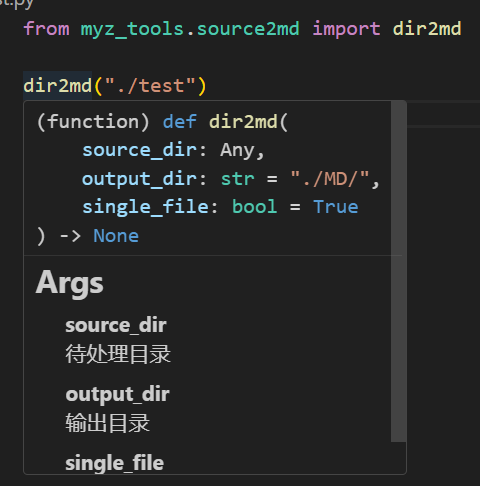
from myz_tools.source2md import dir2md

dir2md("./待处理的目录")

dir2md会自动检查此目录下的所有的python文件并且生成文档，完整参数可以鼠标放到上面查看

库内所有函数目录

文件名称: common_maths.py

函数部分：

函数create_dir

在指定路径下创建名称为{dir_name}的文件夹
Args:
    dir_name: 文件夹名称
    path: 要创建文件夹的路径，默认为当前路径

Returns:
    无

函数get_max_diff

参数：
    two_dimensional_array: 二维数组
返回值：
    每一列里面最大值和最小值的差值，类型是一个一维数组
功能：
    传入一个二维数组，函数返回每一列里面最大值和最小值的差值。

函数remove_outliers_iqr

参数：
    data: 二维数组
返回值：
    去除异常值后的二维数组和有效的行索引，类型是一个元组
功能：
    四分位距法去除传入的二维数组中的异常值，注意是对于每一列来说的自己的异常值

函数export_to_csv

参数：
    array_data: 二维数组，要保存的数据
    file_name: 字符串，CSV文件的名称（不包含扩展名）
    output_directory: 字符串，保存文件的目录路径，默认为当前目录
返回：
    None
功能：
    将给定的二维数组保存到指定目录中的CSV文件。如果文件已存在，则追加数据，并在每次写入时添加空行作为分隔符。

函数generate_2d_combinations_iter

功能：
    传入一个三维数组，返回每个二维数组的所有元素组合的迭代器。如果设置了 `test_first_group` 参数True,
    则仅返回第一个二维数组的组合。

参数：
    data_3d (list): 一个三维列表，每个元素都是一个二维列表，表示多个二维数组。
    test_first_group (bool): 是否只生成第一个二维数组的组合。默认为 False。

返回值：
    generator: 一个生成器对象，按需生成每个二维数组的所有元素组合。

异常：
    ValueError: 如果输入的数据不是三维列表，则抛出异常。

示例：
    >>> data = [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]
    >>> result_iter = generate_2d_combinations_iter(data)
    >>> for combinations in result_iter:
            # 每次拿到是一个二维列表的组合
    ...     print(list(combinations)) # [(1, 3), (1, 4), (2, 3), (2, 4)]
    下一次
    [(5, 7), (5, 8), (6, 7), (6, 8)]


    >>> result_iter = generate_2d_combinations_iter(data, test_first_group=True)
    >>> print(list(next(result_iter)))
    [(1, 3), (1, 4), (2, 3), (2, 4)]

函数generate_row_permutations

功能：
    传入一个二维数组，返回该二维数组中每一行元素所有可能的排列组合。


参数：
    data_2d (list): 一个二维列表，表示多个行数据。

返回值：
    generator: 生成器对象，按需生成每一行的所有排列组合并组合成二维数组。

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> permutations = generate_row_permutations(data)
    >>> for perm in permutations:
    ...     print(perm)
    [[1, 2], [3, 4]]
    [[1, 2], [4, 3]]
    [[2, 1], [3, 4]]
    [[2, 1], [4, 3]]

函数calculate_total_permutations

功能：
    计算并返回二维数组中所有行的排列组合总数。

参数：
    data_2d (list): 一个二维列表，表示多个行数据。

返回值：
    int: 所有行排列组合的总数。

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> total = calculate_total_permutations(data)
    >>> print(total)
    4

函数display_combinations

功能：
    打印二维数组中前 N 个排列组合，以检测组合生成的正确性。

参数：
    data_2d (list): 一个二维列表，表示多个行数据。
    N (int): 要打印的组合数量，默认为 5。

返回值：
    None

异常：
    ValueError: 如果输入的二维数组为空或某行为空，则抛出异常。

示例：
    >>> data = [[1, 2], [3, 4]]
    >>> display_combinations(data, N=2)
    [1, 2]
    [3, 4]

    [1, 2]
    [4, 3]

函数evaluate_list_similarity

功能：
    评估列表中元素间的差异与给定值 `n` 的接近程度。支持不同的评分方法，例如均方误差 (MSE)、绝对误差等。
    三种方式都是得分越小表示列表元素与目标值的接近程度越高
参数：
    lst (list of int/float): 需要评估的数字列表。
    n (int/float): 用于比较的参考值，计算差异的目标值。
    method (str): 选择的评分方法。支持 'MSE'（均方误差）、'MAE'（平均绝对误差）、'total_score'（总分）等。

返回值：
    float: 计算得出的评分值。

异常：
    ValueError: 如果输入的 `lst` 不是列表或 `n` 不是整数或浮点数，则抛出异常。
    TypeError: 如果 `lst` 中的元素不是整数或浮点数，则抛出异常。
    ValueError: 如果选择的评分方法不被支持，则抛出异常。

示例：
    >>> lst = [1, 3, 6, 10]
    >>> n = 2
    >>> score = evaluate_list_similarity(lst, n, method='MSE')
    >>> print(score)

    >>> score = evaluate_list_similarity(lst, n, method='MAE')
    >>> print(score)

函数check_unique

功能：
    检查传入的二维数组中的每个元素是否都是唯一的。如果所有元素唯一，返回 True；否则，返回 False。

参数：
    data (list of list): 一个二维列表，其中包含需要检查的元素。

返回值：
    bool: 如果所有元素都唯一，返回 True；否则，返回 False。

异常：
    TypeError: 如果输入的 `data` 不是一个二维列表，或包含非列表的元素，则抛出异常。

示例：
    >>> data = [[1, 2, 3], [4, 5, 6]]
    >>> check_unique(data)
    True

    >>> data = [[1, 2, 3], [3, 4, 5]]
    >>> check_unique(data)
    False

文件名称: source2md.py

函数部分：

函数dir2md

Args:
    source_dir: 待处理目录
    output_dir: 输出目录
    single_file: 是否将所有文件放到一个md文件中

函数extract_info

功能：
    解析python文件，提取函数和类信息
Args:
    file_path: 待处理文件路径
Returns:
    function_docs: 函数信息
    class_info: 类信息

函数all_save_markdown

功能：
    将提取的函数和类信息保存为markdown文件
Args:
    file_path: 待处理文件路径
    output_path: 保存路径
    function_docs: 函数信息
    class_info: 类信息
Returns:
    无

函数all2md

功能：调用，将一个python文件中的函数和类信息提取出来，并保存为markdown文件
Args:
    file_path: 字符串，python文件的路径
    output_path: 字符串，markdown文件的保存路径
Returns:
    无

函数extract_function_docs_from_file

从 Python 文件中提取函数的 docstring（注释部分）。

参数:
    file_path: 字符串，Python 文件的路径。

返回:
    字典，键为函数名，值为函数的 docstring。

函数save_docs_to_markdown

将函数的 docstring 保存到 Markdown 文件中。

参数:
    docs: 字典，包含函数名和 docstring 的映射。
    output_path: 字符串，Markdown 文件的保存路径。

函数pyFun2md

将 Python 文件中提取 docstring 并保存为 Markdown 文件。

参数:
    source_file: 字符串，源 Python 文件的路径。
    output_md: 字符串，输出 Markdown 文件的路径。

仓库的链接

如果使用中有问题或者是需要别的什么算法，欢迎到
Issues · yi/myz_tools - Gitee.com提Issues，我会逐个看过去的