题目

t(t<=20)组h里，每次给定一棵n(n<=2e5)个点的，点1为根的有根树，

定义树的价值为，

其中，，dep为深度，1号点的深度为0

而a数组待确定，对于所有的种方案，你要使树的价值最大，

问满足树的价值最大的前提下，有多少种方案是符合要求的，取模998244353

思路来源

mouhua

题解

暴力dp是O(n^2)的，不能接受，

而分治ntt有一个max和更新方案的操作，不是很会写

首先每一位是独立的，对于ai∈{0,1}求一下方案，然后对其求k次幂即可，

然后发现局部贪心是可行的，对每个子树而言，每一位1的个数和0的个数尽可能一样

如果一个子树大小是偶数，那么必然是能做到一样的

如果是奇数的话，你需要把那些奇数的儿子连带着你一起，取一半出来

然后发现偶数选一半的时候，选前一半和选后一半方案统计了两次，

前一半是0和后一半是0都统计了，所以不用再乘2了

而当奇数选一半的时候，多的那半选0和少的那半选0是不同的方案，

目前只是把少的那半的点选出来了，0/1并没有决定，

但是这个0/1受上面后来的决策影响，

如果后面的决策是偶数的，两种情况就被包含在内

如果到根的时候还是奇数的，那么相当于最终没有决定是多的这半是0还是1，将答案乘2即可

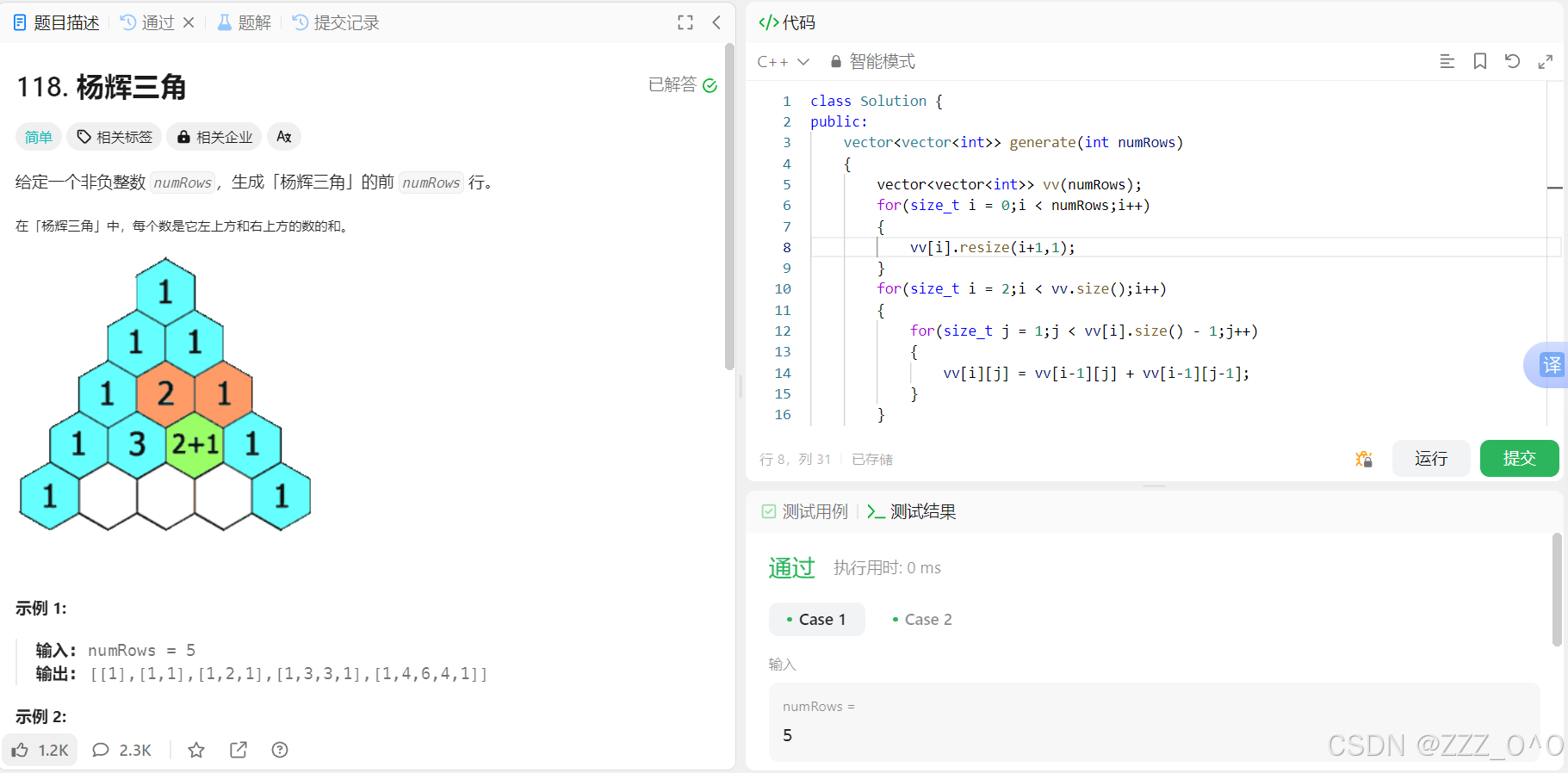
代码

//#include <bits/stdc++.h>
#include<iostream>
#include<vector>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e5+10,mod=998244353;
int Finv[N],fac[N],inv[N],sz[N];
int t,n,k,f,dp[N];
vector<int>e[N];
int modpow(int x,int n,int mod){
	int res=1;
	for(;n;x=1ll*x*x%mod,n>>=1)
	if(n&1)res=1ll*res*x%mod;
	return res;
}
void init(int n){ //n<N
    inv[1]=1;
    for(int i=2;i<=n;++i)inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
	fac[0]=Finv[0]=1;
	for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
	//Finv[n]=modpow(fac[n],mod-2,mod);
	//for(int i=n-1;i>=1;--i)Finv[i]=1ll*Finv[i+1]*(i+1)%mod;
}
int C(int n,int m){
	if(m<0||m>n)return 0;
	return 1ll*fac[n]*Finv[n-m]%mod*Finv[m]%mod;
}
void dfs(int u){
    dp[u]=1;
    sz[u]=1;
    int cnt=1;
    for(auto &v:e[u]){
        dfs(v);
        sz[u]+=sz[v];
        if(sz[v]%2)cnt++;
        dp[u]=1ll*dp[u]*dp[v]%mod;
    }
    dp[u]=1ll*dp[u]%mod*C(cnt,cnt/2)%mod;
    //printf("u:%d dp:%d\n",u,dp[u]);
}
int main(){
    init(N-5);
    sci(t);
    while(t--){
        sci(n),sci(k);
        rep(i,1,n){
            e[i].clear();
        }
        rep(i,2,n){
            sci(f);
            e[f].pb(i);
        }
        dfs(1);
        if(sz[1]&1)dp[1]=2ll*dp[1]%mod;
        int ans=modpow(dp[1],k,mod);
        pte(ans);
    }
    return 0;
}