目录
前言
一. 凸\凹透镜
1 凸透镜
1.1 凸透镜成像
1.2 物距\像距
1.3 凸透镜成像规律
2. 凹透镜
2.1 凹透镜成像规律
二. 相机
相机镜头
前言
平日里总是时不时地听到别人讲起一些摄影相关的术语,比如:光圈、焦距、等效焦距、EV、画幅、景深、快门、ISO等等。但是不解其中意,更不知它们代表的实际物理意义是什么。
为了了解这些相关的知识点,个人搜罗网上的资料进行学习,这篇博客是个人学习过程中的一些梳理、总结,算是一篇学习笔记,其目的也主要是厘清相关的概念,如果其中有不对的地方,也欢迎各位看官们提出指正。
我们都知道相机就是利用了凸透镜的成像原理,这一节里先回顾一下关于中学的时候学过的透镜这部分相关知识。
一. 凸\凹透镜
在中学物理时就有学过透镜相关的知识了(不过估计大部分知识点已经还给物理老师了😂),到现在可能脑海里只剩下零星的印象,这一篇先回顾一下透镜相关的一些基本知识,为后面的知识做铺垫。
光的折射:光从一种介质斜射入另一种介质时,传播方向会发生改变,从而使光线在不同介质的交界处发生偏折。
透镜是由透明物质(如玻璃、水晶等)制成的一种光学元件, 它正是根据光的折射规律制成的,通过透镜表面的弯曲,改变光线入射的角度,从而改变光线的传播方向。
1 凸透镜
凸透镜的特点是:中间厚、边缘薄,对光有会聚作用。无论时隔多久,相信大家对下面这张图一定还是印象深刻的,这张图其中涉及到几个基本的光学概念:光心、主光轴、焦点、焦距。
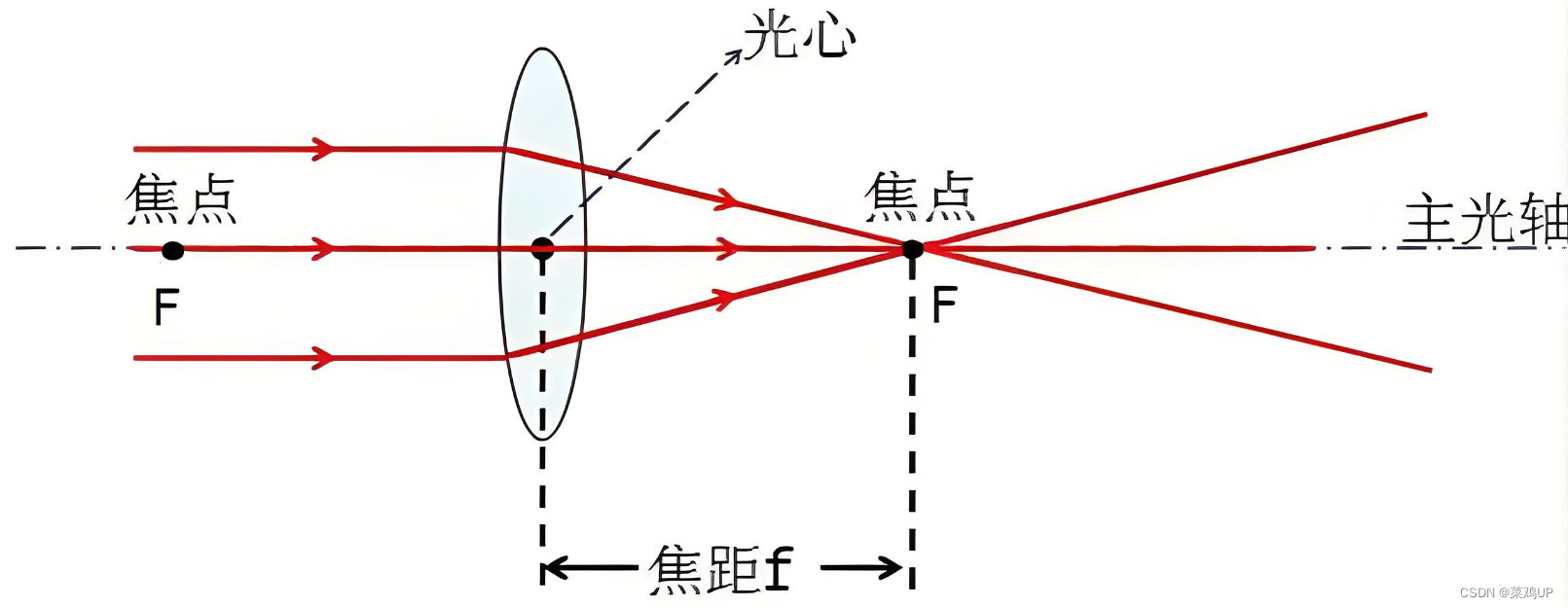
- 光心:凸透镜的中心点是透镜的光心,也就是凸透镜的光学中心
- 主光轴:凸透镜两个球面的球心的连线,称为此透镜的主光轴
- 焦点(F):将平行光(如太阳光)平行于主光轴射入凸透镜,光在透镜的两面分别经过一次折射后,会交汇在主光轴上的一个点,此点就叫做凸透镜的焦点
- 焦距(f): 焦点到光心的距离就是该凸透镜的焦距
1.1 凸透镜成像
关于凸透镜成像,先以一个点光源为例子,一个点光源会从各个方向发出光线,会有一部分进入凸透镜,进入凸透镜的这部分光线经过凸透镜的折射后,如同一束光锥,完美会聚到一个交叉点,这个交叉点点就是成像的位置,如下图所示。
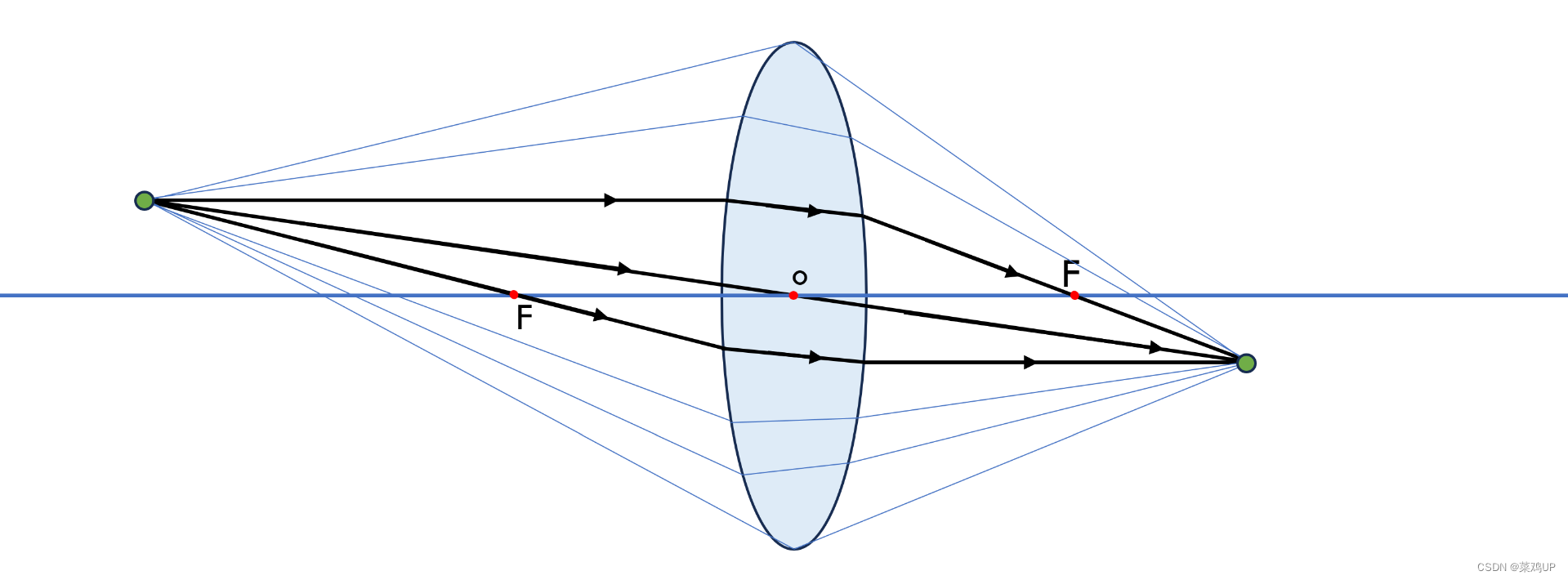
图中所有的光路里,有3条特殊的光路:一条是经过光心的;一条是平行于主光轴的光线;还有一条是通过焦点入射的光线。这三条光线的特点是:
- 经过光心的光线:光路方向不会发生改变,沿直线传播
- 平行于光轴的光线:光路会经过焦点
- 通过焦点的光线:通过焦点的光线经透镜折射后平行于主光轴
这三条光路必交会在像的位置,所以由这3条光路及其交会的点,便可画出其他入射角度光线的光路图,因为其他角度的入射光线也会交会在像点。
一个物体是由无数个点光源组成的,最终所有的点光源都投射在一个平面上
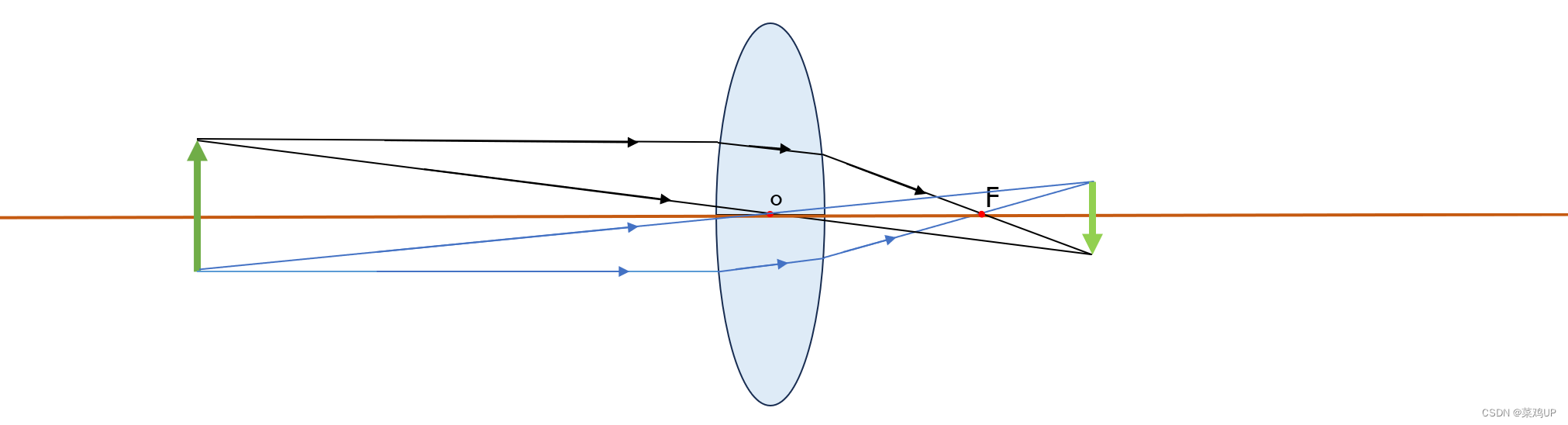
1.2 物距\像距
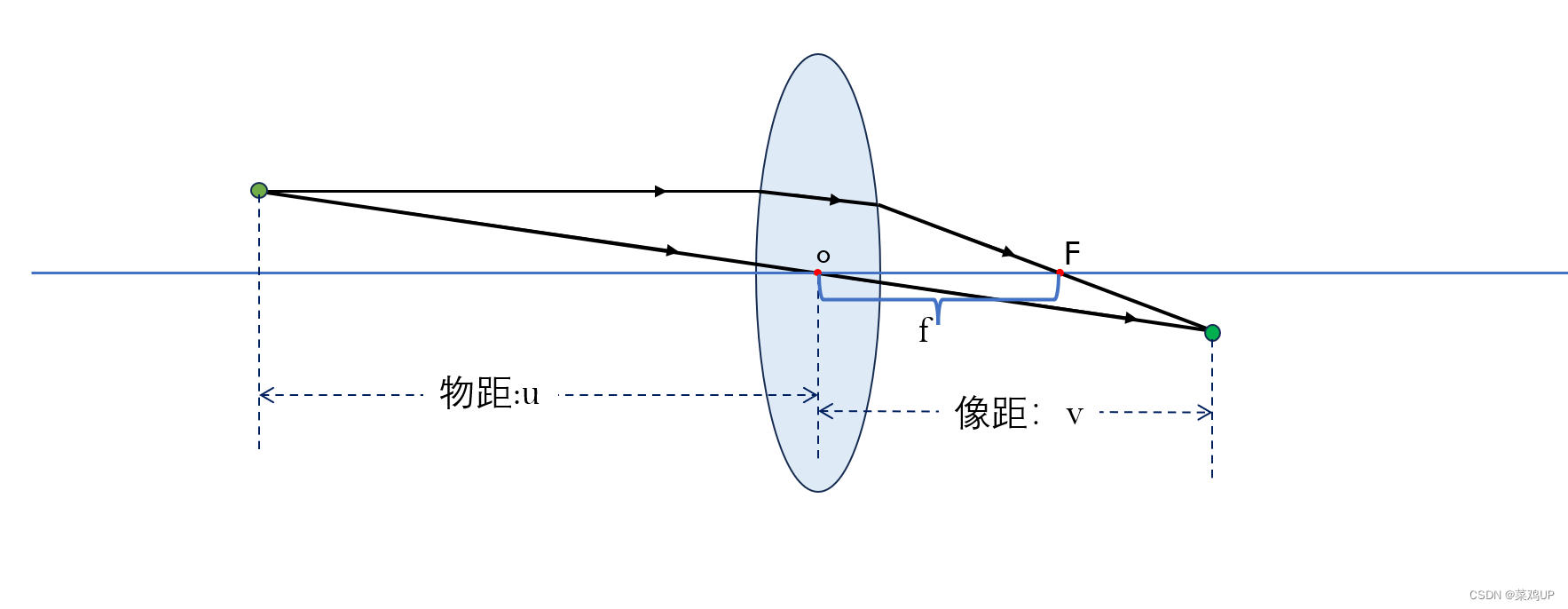
- 物距:物体到透镜光心的距离,一般用u表示。
- 像距:像到透镜光心之间的距离,一般用v表。
物距(u)、像距(v)和焦距(f)三者关系满足高斯公式 :
1.3 凸透镜成像规律
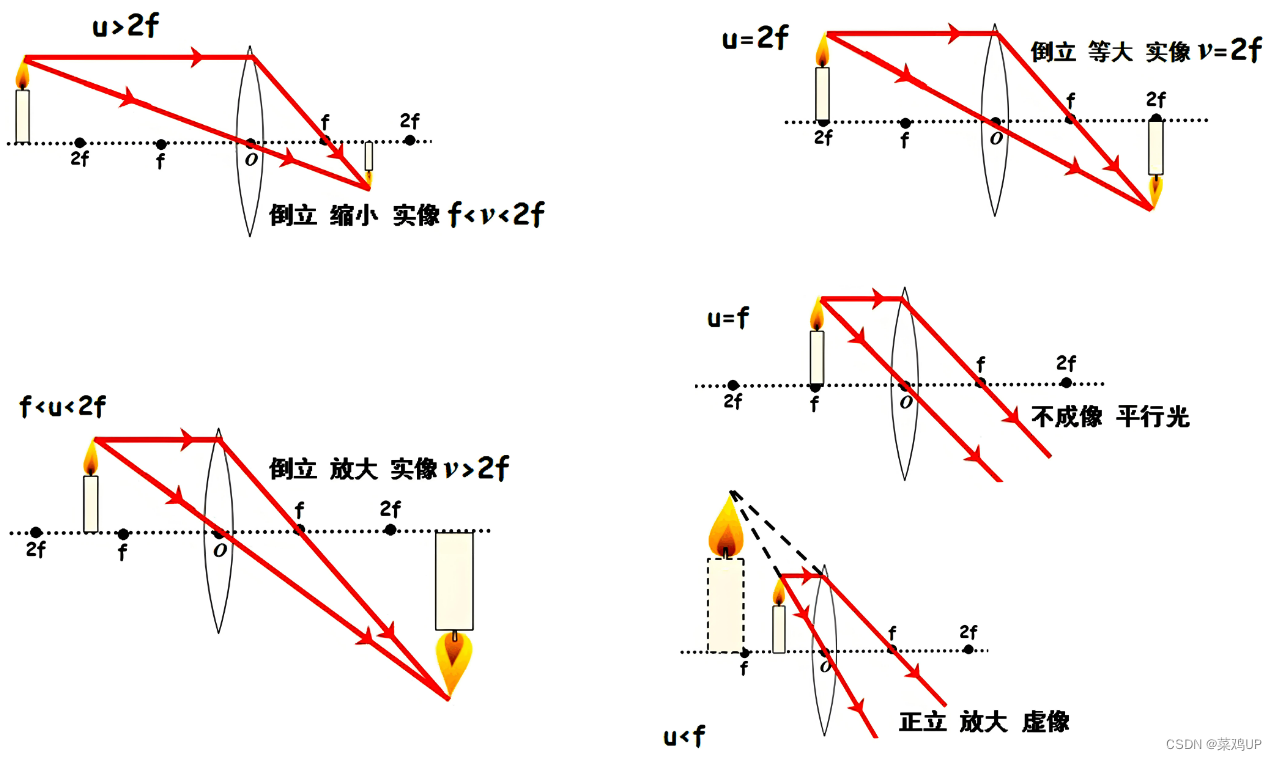
可能大家脑海里还依稀记得上学时有这样一张关于凸透镜成像规律的表 ,表里面总结了关于物距,像距,像的虚实、正倒、大小规律这些:
| 物距 u (物体到凸透镜的距离) | 像距 v (像到凸透镜的距离) | 像的 大小 | 像的 正倒 | 像的 虚实 | 应用 实例 |
| u>2f | 2f>v>f | 缩小 | 倒立 | 实像 | 照相机 |
| u=2f | v=2f | 等大 | 倒立 | 实像 | 测焦距 |
| 2f>u>f | v>2f | 放大 | 倒立 | 实像 | 放映机 幻灯机 投影机 |
| u=f | 无(平行 v无限大) | 无 | 无 | 无 | 探照灯 |
| u<f | 无 | 放大 | 正立 | 虚像 | 放大镜 |
- 实像:由实际光线汇聚而成,能在光屏上呈现的像
- 虚像:不是实际光线汇聚而成,不能在光屏上呈现的像,但能被看见
可以发现只有当物距大于焦距时,才会成实像。当然上面表中的这些规律都是可以根据画光路图总结出来的,如下图所示,看图会更有感觉。
2. 凹透镜
凹透镜是中间薄、边缘后的透镜,对入射光具有发散作用。同样的,大家脑海里应该也还有关于这幅图的印象吧,这是平行光入射到凹透镜后的光路示意图。
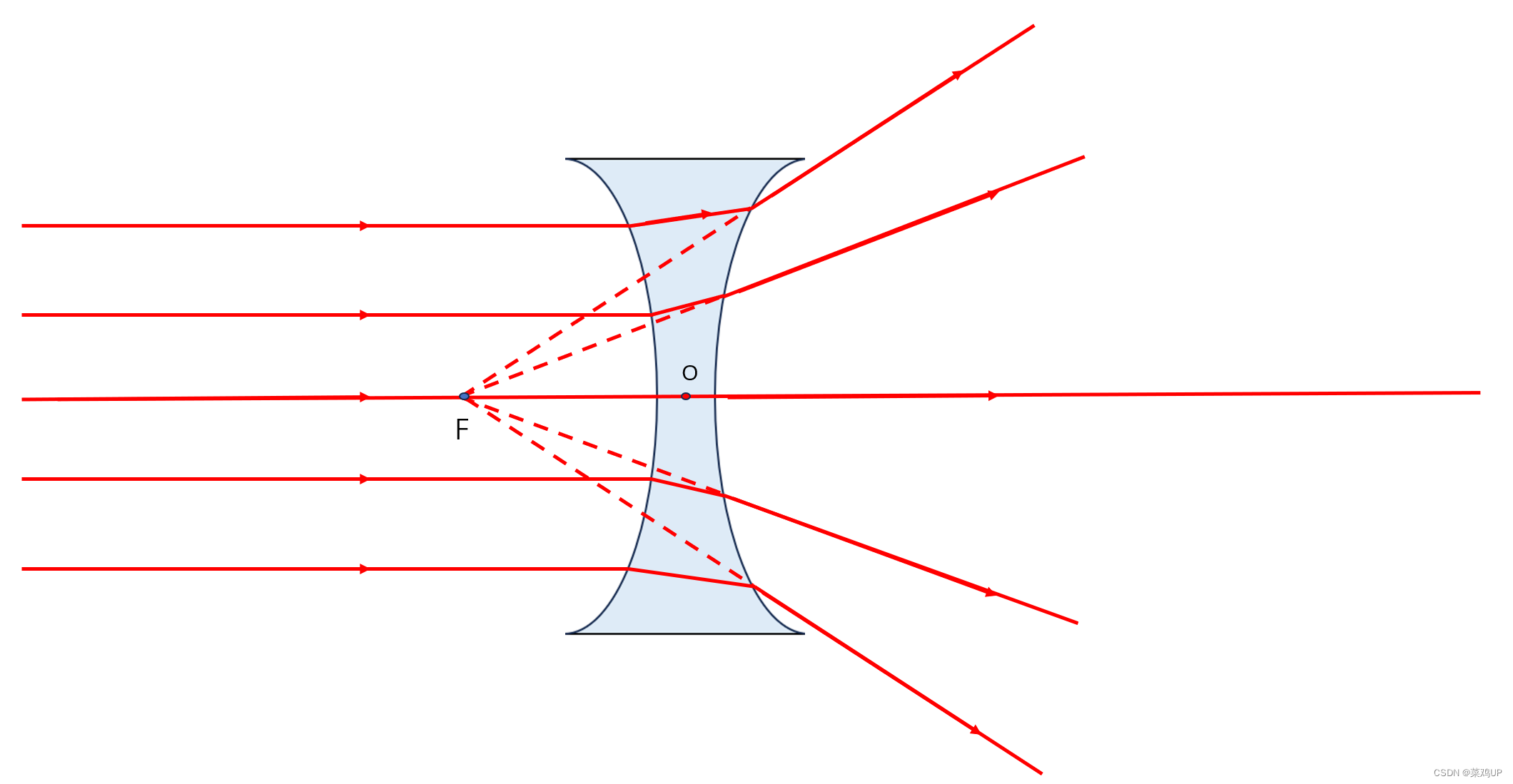
平行入射光线经过凹透镜后,其发散光的反向延长线交于一点,即凹透镜的虚焦点。其中有3条特殊的光线:
- 通过光心的光线传播方向不会发生改变
- 平行于光轴的入射光线经过凹透镜后折射后的折射光线,其反向延长线经过焦点
- 延长线通过焦点的光线,经凹透镜后平行于主光轴
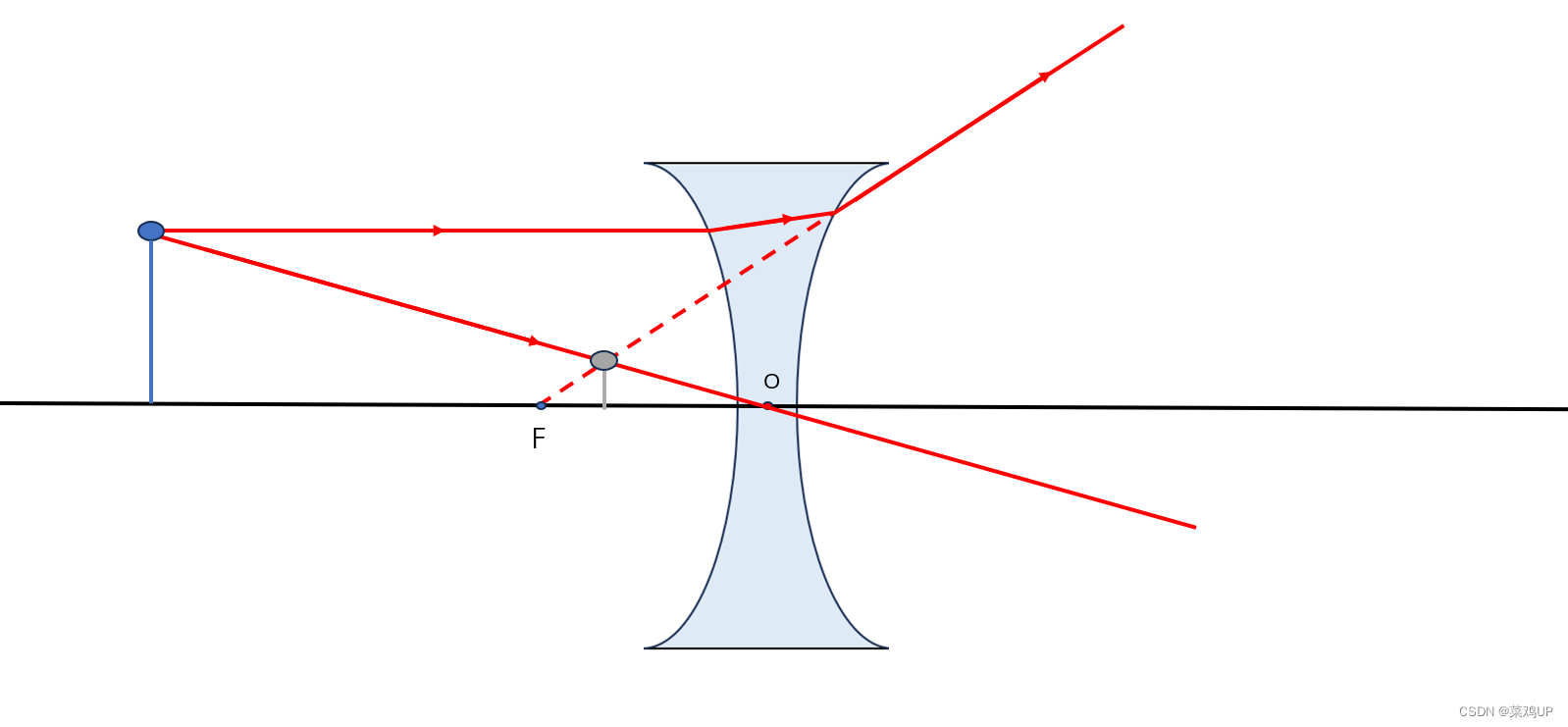
2.1 凹透镜成像规律
实际物体经过凹透镜成的像总是正立的、缩小的虚像,物和像在同一侧,虚像的位置在一倍焦距以内。
二. 相机
照相机运用的就是凸透镜的成像规律。照相机从物理结构上可分为镜头和机身两部分,镜头部分就相当于是凸透镜,机身部分则含有感光元件(胶卷或是图像传感器(CCD or CMOS)),相当于光屏。
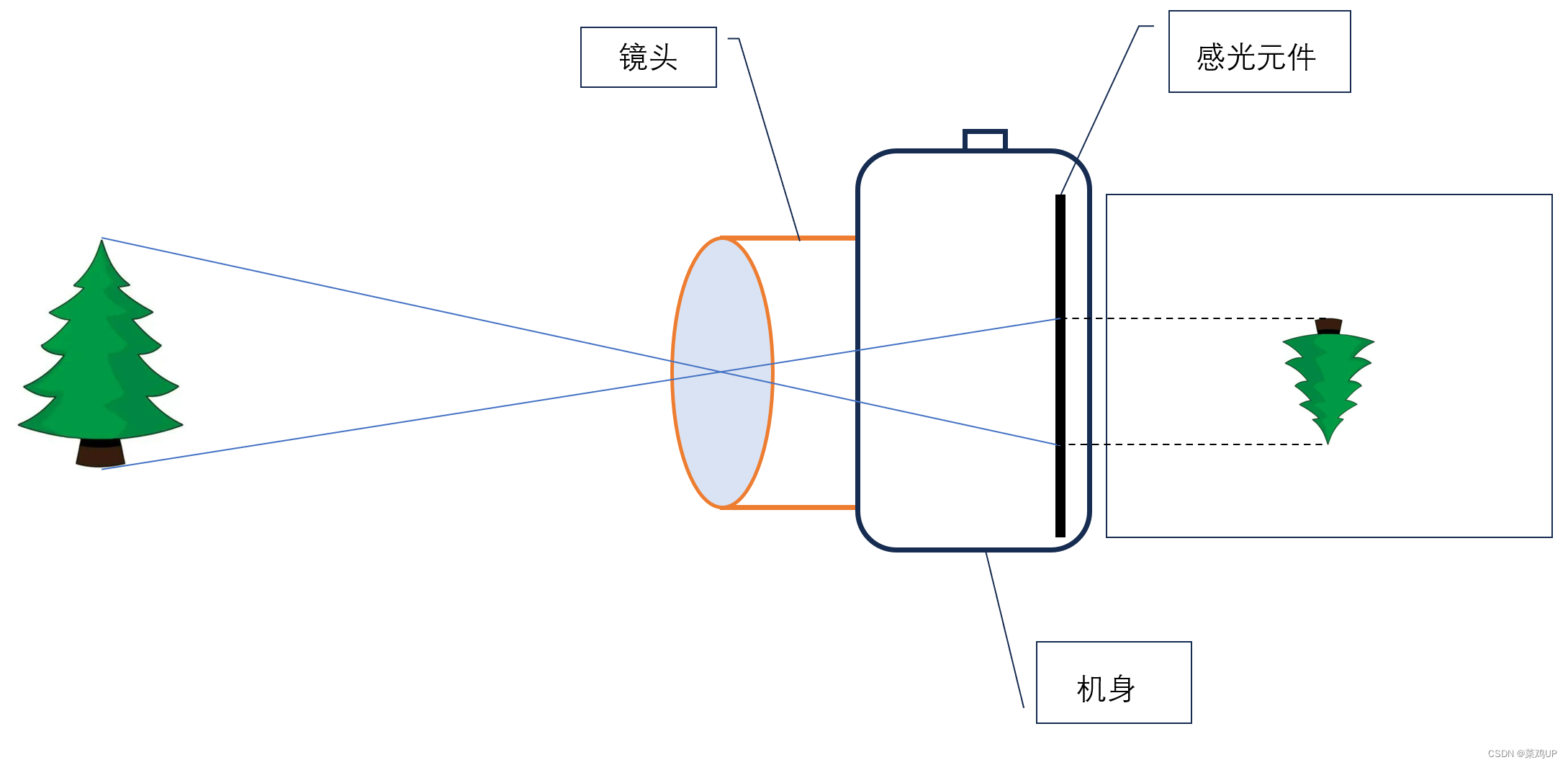
通过镜头(一个凸透镜)的光线聚焦在感光元件上, 这些感光元器件可以捕捉到光线,并将其转换为电信号,这些信号会随后再被ISP处理,最终形成我们可以看到的图像。
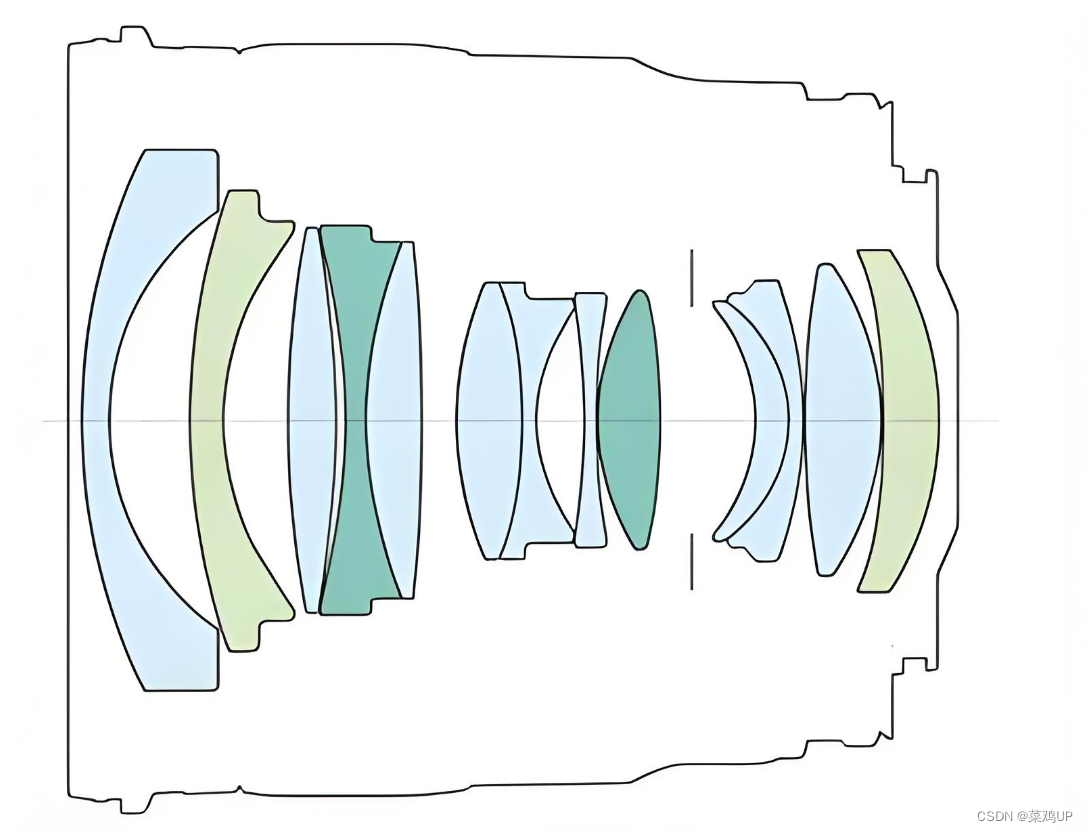
相机镜头
真实的相机镜头是由好几组镜片组成的,其目的是为了更好的会聚光线,优化成像品质,但其根本上还是利用了凸透镜的成像原理。所以后面为了方便理解,大多时候可以先把相机的镜头简化成是一个凸透镜,它有一个光学中心。