343. 整数拆分
题目链接:. - 力扣(LeetCode)
讲解视频:
动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分
题目描述:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
解题思路:
1. 状态表示:
dp[i]表示将整数i拆分成至少两个正整数的和之后,这些正整数乘积的最大值。2. 状态转移方程:
代码中使用了两层循环来计算
dp[i]。第一层循环从i = 3开始,表示我们从 3 开始计算每个i的最大乘积。第二层循环遍历j从 1 到i-1,表示将i拆分成j和i-j的和,然后我们有两种选择:
- 不进一步拆分
i-j,直接计算j * (i-j)。- 继续拆分
i-j,这时我们使用j * dp[i-j]。对于每个
i,我们在dp[i]中取上述两种选择的最大值。 因此,状态转移方程为:dp[i]=max(dp[i],max(j×(i−j),j×dp[i−j]))3. 初始化:
初始化的时候,我们可以认为每个
dp[i]都至少为 1,这是因为任何一个整数i的最小拆分乘积至少为 1。4. 填表顺序:
使用从左往右的顺序填充
dp表,这样可以确保在计算dp[i]时,dp[i-j]已经计算过。5. 返回值:
最终返回
dp[n]
代码:
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n+1,1);
for(int i = 3; i <= n; i++)
for(int j = 1; j < i; j++)
dp[i] = max(dp[i], max(j * (i-j), j * dp[i-j]));
return dp[n];
}
};96.不同的二叉搜索树
题目链接:. - 力扣(LeetCode)
讲解视频:
动态规划找到子状态之间的关系很重要!| LeetCode:96.不同的二叉搜索树
题目描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
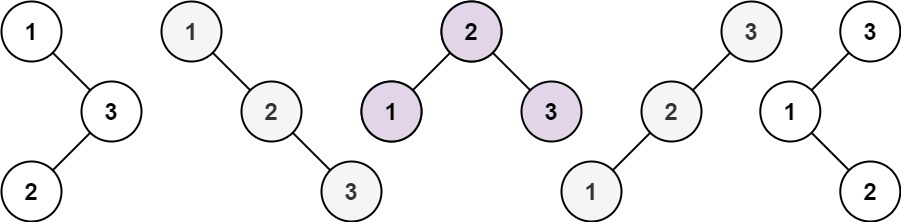
输入:n = 3 输出:5
解题思路:
1. 状态表示:
根据「拆分出相同子问题」的方式,抽象出来一个状态表示:
当我们在求个数为 n 的 BST 的个数的时候,当确定一个根节点之后,左右子树的结点「个数」也确定了。此时左右子树就会变成相同的子问题,因此我们可以这样定义状态表示:
dp[i] 表示:当结点的数量为 i 个的时候,一共有多少颗 BST 。
2. 状态转移方程:
对于 dp[i] ,此时我们已经有 i 个结点了,为了方便叙述,我们将这 i 个结点排好序,并且编
上 1, 2, 3, 4, 5.....i 的编号。
那么,对于所有不同的 BST ,我们可以按照下面的划分规则,分成不同的 i 类:「按照不同的头结点来分类」。分类结果就是:
- 头结点为 1 号结点的所有 BST
- 头结点为 2 号结点的所有 BST
- ......
如果我们能求出「每一类中的 BST 的数量」,将所有类的 BST 数量累加在一起,就是最后结果。接下来选择「头结点为 j 号」的结点,来分析这 i 类 BST 的通用求法。
如果选择「 j 号结点来作为头结点」,根据 BST 的定义:
- j 号结点的「左子树」的结点编号应该在 [1, j - 1] 之间,一共有 j - 1 个结点。那么 j 号结点作为头结点的话,它的「左子树的种类」就有 dp[j - 1] 种(回顾一下我们 dp 数组的定义哈);
- j 号结点的「右子树」的结点编号应该在 [j + 1, i] 之间,一共有 i - j 个结点。那么 j 号结点作为头结点的话,它的「右子树的种类」就有 dp[i - j] 种;
根据「排列组合」的原理可得: j 号结点作为头结点的 BST 的种类一共有 dp[j - 1] *dp[i - j] 种!因此,我们只要把「不同头结点的 BST 数量」累加在一起,就能得到 dp[i] 的值: dp[i]
+= dp[j - 1] * dp[i - j] ( 1 <= j <= i) 。「注意用的是 += ,并且 j 从 1 变化到 i 」。
3. 初始化:
我们注意到,每一个状态转移里面的 j - 1 和 i - j 都是小于 i 的,并且可能会用到前一
个的状态(当 i = 1,j = 1 的时候,要用到 dp[0] 的数据)。因此要先把第一个元素初始
化。当 i = 0 的时候,表示一颗空树,「空树也是一颗二叉搜索树」,因此 dp[0] = 1 。
4. 填表顺序:
根据「状态转移方程」,易得「从左往右」。
5. 返回值:
根据「状态表示」,我们要返回的是 dp[n] 的值。
代码:
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n+1,0);
dp[0] = 1;
for(int i = 1; i <= n; i++)
for(int j = 0; j < i; j++)
dp[i] += dp[j]*dp[i-j-1];
return dp[n];
}
};01背包理论
题目链接:01背包理论
讲解视频:
带你学透0-1背包问题!
题目描述:
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
解题思路:
1. 状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积「不超过」 j ,所有的选法中,能挑选出来
的最大价值。
2. 状态转移方程:
线性 dp 状态转移方程分析方式,一般都是根据「最后一步」的状况,来分情况讨论:
- 不选第 i 个物品:相当于就是去前 i - 1 个物品中挑选,并且总体积不超过 j 。此时 dp[i][j] = dp[i - 1][j] ;
- 选择第 i 个物品:那么我就只能去前 i - 1 个物品中,挑选总体积不超过 j - v[i]的物品。此时 dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不一定存在,因此需要特判一下。
综上,状态转移方程为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] +w[i]) 。
3. 初始化:
我们多加一行,方便我们的初始化,此时仅需将第一行初始化为 0 即可。因为什么也不选,也能满足体积不小于 j 的情况,此时的价值为 0 。
4. 填表顺序:
根据「状态转移方程」,我们仅需「从上往下」填表即可。
5. 返回值:
根据「状态表示」,返回 dpn] 。
代码:
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n, m;
cin >> m >> n;
vector<int> space(m+1);
vector<int> value(m+1);
for(int i = 1; i <= m; i++) cin >> space[i];
for(int i = 1; i <= m; i++) cin >> value[i];
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i = 1; i <= m; i++)//物品
{
for(int j = 0; j <= n; j++)//背包容量
{
dp[i][j] = dp[i-1][j];
if(j >= space[i])
dp[i][j] = max(dp[i][j],dp[i-1][j-space[i]]+value[i]);
}
}
cout << dp[m][n];
return 0;
}01背包优化
解题思路:
利用滚动数组来做空间上的优化:
- 利用「滚动数组」优化;
- 直接在「原始代码」上修改。
在01背包问题中,优化的结果为:
- 删掉所有的横坐标;
- 修改一下 j 的遍历顺序-->从右向左,因为防止上一层hai'wei'b数被改变
代码:
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n, m;
cin >> m >> n;
vector<int> space(m+1);
vector<int> value(m+1);
for(int i = 1; i <= m; i++) cin >> space[i];
for(int i = 1; i <= m; i++) cin >> value[i];
vector<int> dp(n+1);
for(int i = 1; i <= m; i++)//物品
for(int j = n; j >= space[i]; j--)//背包容量
dp[j] = max(dp[j],dp[j-space[i]]+value[i]);
cout << dp[n];
return 0;
}